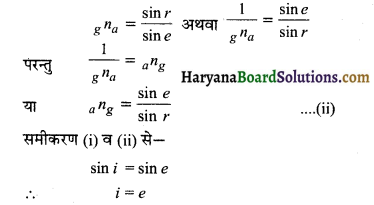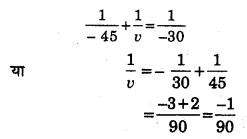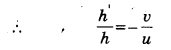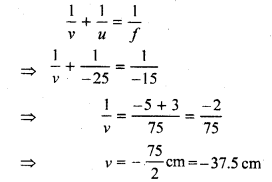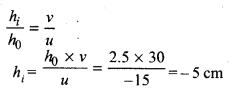Haryana State Board HBSE 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन Important Questions and Answers.
Haryana Board 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन
अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
क्या प्रकाश को आँखों से देखा जा सकता हैं ?
उत्तर-
नहीं, प्रकाश की उपस्थिति में अन्य वस्तुओं को देखा जा सकता है परन्तु प्रकाश स्वयं दिखाई नहीं देता।
प्रश्न 2.
प्रकाश किरण के तीक्ष्ण किनारों पर मुड़ने की घटना को क्या कहते हैं?
उत्तर-
विवर्तन।
प्रश्न 3.
विवर्तन की घटना को स्पष्ट करने के लिये प्रकाश किस रूप को प्रदर्शित करता है?
उत्तर-
तरंग (Wave)। .
प्रश्न 4.
प्रकाश के परावर्तन से क्या तात्पर्य है ?
उत्तर-
किसी चमकदार. सतह से प्रकाश किरणों के टकराकर वापस लौटने की घटना को प्रकाश का परावर्तन कहते हैं।
प्रश्न 5.
प्रकाश का परावर्तन कितने प्रकार का होता हैं ?
उत्तर-
प्रकाश का परावर्तन दो प्रकार का होता है-
- नियमित परावर्तन,
- विसरित परावर्तन।
प्रश्न 6.
गोलीय दर्पण किसे कहते हैं ? |RBSE 2015]
उत्तर-
गोलीय दर्पण किसी चमकीले गोले का कटा हुआ भाग होता है जो अन्दर या बाहर से प्रकाश का परावर्तन कर सकता है।

प्रश्न 7.
किसी गोलीय दर्पण की वक्रता त्रिज्या और फोकस दूरी में क्या सम्बन्ध होता है ?
उत्तर-
वक्रता त्रिज्या (R) = 2 x फोकस दूरी (f).
प्रश्न 8.
दर्पण सूत्र क्या है ?
उत्तर-
\(\frac{1}{f}= \frac{1}{v}+\frac{1}{u}\)
प्रश्न 9.
किसी दर्पण द्वारा उत्पन्न आवर्धन का क्या अर्थ है ?
उत्तर-
किसी गोलीय दर्पण द्वारा बने प्रतिबिम्ब का आकार तथा वस्तु के आकार के अनुपात को आवर्धन कहते हैं।
प्रश्न 10.
प्रकाश के परावर्तन के नियम लिखिए।
उत्तर-
- आपतन कोण
- तथा परावर्तन कोण r बराबर होते हैं।
- आपतित किरण, दर्पण’ के आपतन बिन्दु पर अभिलम्ब एवं परावर्तित किरण एक ही तल में होते हैं।
प्रश्न 11.
समतल दर्पण की फोकसदूरी कितनी होती है ?
उत्तर-
समतल दर्पण की फोकस दूरी अनन्त होती है।
प्रश्न 12.
एक अवतल दर्पण के ध्रुव तथा फोकस बिन्दु के बीच रखी वस्तु का प्रतिबिम्ब कहाँ बनेगा ?
उत्तर-
प्रतिबिम्ब दर्पण के पीछे बनेगा। यह सीधा, वस्तु से बड़ा तथा आभासी होगा।
प्रश्न 13.
समतल दर्पण द्वारा बने प्रतिबिम्ब का आवर्धन कितना होता है?
उत्तर-
m = + 1 (आवर्धन)
प्रश्न 14.
गाड़ी की हैडलाइट में कौन-सा दर्पण प्रयुक्त किया जाता है ?
उत्तर-
अवतल दर्पण।
प्रश्न 15.
किस दर्पण द्वारा आवर्धन धनात्मक परन्तु 1 से कम होता है?
उत्तर-
उत्तल दर्पण द्वारा।

प्रश्न 16.
वाहनों के पश्च-दृश्य दर्पण के रूप में प्रयुक्त गोलीय दर्पण का नाम लिखिए। (RBSE 2015)
उत्तर-
उत्तल दर्पण।
प्रश्न 17.
प्रकाश का अपवर्तन किसे कहते हैं ?
उत्तर-
जब प्रकाश की किरण एक माध्यम से दूसरे माध्यम में जाती है, तो विचलित हो जाती है, इस क्रिया को अपवर्तन कहते हैं।
प्रश्न 18.
जब प्रकाश की किरण वायु से पानी में प्रवेश करती है तब क्या होता है ?
उत्तर-
जब प्रकाश की किरण वायु (विरल माध्यम) से पानी (सघन माध्यम) में प्रवेश करती है तो यह अभिलम्ब की ओर मुड़ जाती है। इस कारण से अपवर्तन कोण, आपतित कोण से छोटा होता है।
प्रश्न 19.
अपवर्तन के दो उदाहरण दीजिए।
उत्तर-
- पानी में डूबे सिक्के का ऊपर उठा हुआ दिखाई देना।
- पानी में डूबी लकड़ी टेढ़ी दिखाई देना।
प्रश्न 20.
प्रकाश के अपवर्तन में उसकी आवृत्ति पर क्या प्रभाव पड़ता है ?
उत्तर-
आवृत्ति पर कोई भी प्रभाव नहीं पड़ता है।
प्रश्न 21.
जब प्रकाश विरल माध्यम से सघन माध्यम में प्रवेश करता है, तो उसकी चाल तथा पथ किस प्रकार प्रभावित होते हैं?
उत्तर-
जब प्रकाश किरण विरल माध्यम से सघन माध्यम में जाती है तो वह अभिलम्ब की ओर झुक जायेगी। माध्यम का घनत्व अधिक होने के कारण उसकी चाल कम हो जायेगी।
प्रश्न 22.
जब प्रकाश दो माध्यमों के अन्तरापृष्ठ पर अभिलम्बवत् आपतित होता है तो क्या होता है?
उत्तर-
प्रकाश के पथ पर कोई प्रभाव नहीं पड़ता है।
प्रश्न 23.
अपवर्तनाँक का प्रकाश के वेग से क्या सम्बन्ध है?
उत्तर-

प्रश्न 24.
एक ऐसे पदार्थ का नाम लिखो जिसका अपवर्तनांक सबसे अधिक होता है। .
उत्तर-
हीरा, जिसका अपवर्तनांक 2.42 होता है।
प्रश्न 25.
अपवर्तनांक का क्या मात्रक होता है?
उत्तर-
अपवर्तनांक का कोई भी मात्रक नहीं होता है क्योंकि यह समान राशियों का अनुपात है।
प्रश्न 26.
अपवर्तनांक सम्बन्धी स्नैल का नियम लिखिये।
या
अपवर्तन का नियम लिखिये जो आपतन कोण और अपवर्तन कोण के बीच सम्बन्ध बताता है।
उत्तर-
जब कोई प्रकाश किरण किसी पारदर्शी माध्यम में प्रवेश करती है तो उसके आपतन कोण की ज्या (sin i) तथा अपवर्तन कोण की ज्या (sin r) में एक निश्चित अनुपात होता है जिसे अपवर्तनांक कहते हैं।
प्रश्न 27.
छोटे अक्षरों को पढ़ने हेतु कौन-सा लेंस उपयोग किया जाता है?
उत्तर-
उत्तल लेंस।
प्रश्न 28.
दूर स्थित किसी वस्तु का उत्तल लेंस द्वारा किस प्रकार का प्रतिबिम्ब बनता है ?
उत्तर-
वास्तविक, उल्टा तथा छोटा।
प्रश्न 29.
मुख्य फोकस व प्रकाशिक केन्द्र के बीच की दूरी को क्या कहते हैं ?
उत्तर-
फोकस दूरी (f).

प्रश्न 30.
किस स्थिति में प्रतिबिम्ब वस्तु के आकार के समान होता है ?
उत्तर-
जब वस्तु 2f पर हो।
प्रश्न 31.
जब वस्तु लेंस से अनन्त दूरी पर हो तो प्रतिबिम्ब कैसा बनता है ?
उत्तर-
वास्तविक, उल्टा तथा आकार में वस्तु से छोटा होता है।
प्रश्न 32.
जब वस्तु F और प्रकाशिक केन्द्र के बीच में हो, तो उत्तल लेंस द्वारा बनाया गया प्रतिबिम्ब कहाँ और कैसा बनेगा ?
उत्तर-
उत्तल लेंस के F व प्रकाशिक केन्द्र के बीच रखी वस्तु का प्रतिबिम्ब वस्तु की ओर काल्पनिक और सीधा बनेगा।
प्रश्न 33.
लेंस किसे कहते हैं ? ये कितने प्रकार के होते हैं?
उत्तर-
एक ऐसा पारदर्शक माध्यम जो दो वक्र तलों से घिरा हुआ हो लेंस कहलाता है।
ये दो प्रकार के होते हैं-
- उत्तल लेंस,
- अवतल लेंस।
प्रश्न 34.
लेंस से दूरियाँ किस बिन्दु पर मापी जाती हैं?
उत्तर-
प्रकाशिक केन्द्र से।
प्रश्न 35.
किसी लेंस की क्षमता का क्या अर्थ है ? तथा इसका S.I. मात्रक लिखिये। [CBSE 2015]
उत्तर-
मीटर में व्यक्त की गई लेंस की फोकस दूरी (f) के व्युत्क्रम को लेंस की क्षमता (P) कहते हैं।
P = \(\frac{1}{f(\mathrm{~m} \text { में })} \text { या } \frac{100}{f(\mathrm{~cm} \text { में })} \)
तथा S.I. मात्रक डायोप्टर (D) होता हैं।
प्रश्न 36.
लेंस को सूत्र लिखिए।
उत्तर-
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
प्रश्न 37.
कौन सा लेंस अभिसारी लेंस कहलाता हैं?
उत्तर-
उत्तल लेंस।
प्रश्न 38.
किस लेंस को अपसारी लेंस कहते हैं ?
उत्तर-
अवतल लेंस को।
प्रश्न 39.
अभिसारी लेंस की क्षमता धनात्मक होती है या ऋणात्मक ?
उत्तर-
अभिसारी लेंस की क्षमता धनात्मक होती है क्योंकि इसकी फोकस दूरी धनात्मक होती है।

प्रश्न 40.
किस लेंस का आवर्धन सदैव 1 से कम होता
उत्तर-
अवतल लेंस का।।
प्रश्न 41.
सम्पर्क में रखे दो लेंसों की क्षमताएँ P1 व P2 हैं। संयुक्त लेंस की क्षमता क्या होगी?
उत्तर-
क्षमता P = P1 + P2.
प्रश्न 42.
एक उत्तल लेंस वस्तु का सीधा तथा आभासी प्रतिबिम्ब बनाता है। वस्तु कहाँ स्थित होगी ? ।
उत्तर-
मुख्य फोकस व लेंस के प्रकाशिक केन्द्र के मध्य रखी है।
प्रश्न 43.
5 cm ऊँची वस्तु उत्तल लेंस से 2f दूरी पर रखी है। प्रतिबिम्ब की लम्बाई क्या होगी ?
उत्तर-
5 cm.
प्रश्न 44.
यदि किसी लेंस की क्षमता 0.25D है तो उस लेंस का नाम बताओ?
उत्तर-
अवतल लेंस।
लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
ड्राइवर का रात्रि में किस प्रकार के प्रकाश पुंज का प्रयोग करना चाहिए एवं क्यों? स्पष्ट कीजिये। (RBSE 2016)
उत्तर-
ड्राइवर को रात्रि में कम तीव्रता वाले प्रकाश पुंज का प्रयोग करना चाहिये। कम तीव्रता वाले प्रकाश पुंज का प्रयोग करने से सामने से आने वाली वाहन के ड्राइवर की आँखों में रोशनी नहीं पड़ती, उसे सामने स्पष्ट दिखायी देता है। इस प्रकार से आपस में दुर्घटनाएँ होने से बच जाते हैं। कम तीव्रता वाले प्रकाश पुंज रात में वाहन चलाने के लिए बहुत मदद करता है।
प्रश्न 2.
समतल दर्पण द्वारा बने प्रतिबिम्ब की विशेषताएँ लिखिए।
उत्तर-
समतल दर्पण द्वारा बने प्रतिबिम्ब की निम्नलिखित विशेषताएँ होती हैं
- यह सीधा तथा आभासी होता है तथा वस्तु के आकार के बराबर होता है।
- यह दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी दूरी पर वस्तु दर्पण के सामने होती है।
- यह पार्श्व परिवर्तित होता है।
प्रश्न 3.
प्रतिबिम्ब से क्या तात्पर्य है ? आभासी तथा वास्तविक प्रतिबिम्ब में क्या अन्तर है ? [RBSE 2015]
उत्तर-
प्रतिबिम्ब-दर्पण के सामने रखी वस्तु की दर्पण में जो आकृति बन जाती है उस आकृति को वस्तु का प्रतिबिम्ब कहते हैं। अतः जब प्रकाश किरणें किसी बिन्दु से चलकर परावर्तन के पश्चात् (दर्पण में) अथवा लेंस में अपवर्तित होकर किसी दूसरे बिन्दु पर मिलती हैं अथवा किसी दूसरे बिन्दु से आती हुई प्रतीत होती हैं तो इस दूसरे बिन्दु को पहले बिन्दु का प्रतिबिम्ब कहते हैं।
प्रतिबिम्ब दो प्रकार के होते हैं-
- वास्तविक प्रतिबिम्ब-यदि किसी बिन्दु या वस्तु से चलने वाली प्रकाश किरणें परावर्तन (अथवा अपवर्तन)के पश्चात् किसी बिन्दु पर वास्तव में मिलती हैं तो इस दूसरे बिन्दु पर बने प्रतिबिम्ब को वस्तु का वास्तविक प्रतिबिम्ब . कहते हैं। वास्तविक प्रतिबिम्ब को पर्दे पर प्राप्त किया जा सकता है।
- आभासी प्रतिबिम्ब-यदि किसी बिन्दु से चलने वाली प्रकाश किरणें परावर्तन (अथवा अपवर्तन) के पश्चात् किसी दूसरे बिन्दु पर वास्तव में नहीं मिलती हैं, बल्कि दूसरे बिन्दु से आती हुई प्रतीत होती हैं तो जहाँ से किरणें आती हुई प्रतीत होती हैं, बने प्रतिबिम्ब को वस्तु का आभासी प्रतिबिम्ब कहते हैं। इस प्रतिबिम्ब को पर्दे पर प्राप्त नहीं किया जा सकता है।
प्रश्न 4.
दर्पणों की पहचान किस प्रकार करते हैं?
उत्तर-
दर्पणों की पहचान दो प्रकार से करते हैं-
(i) स्पर्श करके-दर्पणों की पहचान के लिए समतल पैमाने का उपयोग करते हैं। पैमाने को दर्पण पर रखने से यदि पैमाना दर्पण को सभी जगह स्पर्श करे तो दर्पण समतल दर्पण होता है। यदि पैमाना दर्पण को किनारों पर स्पर्श करे तथा दर्पण के बीच का भाग कुछ दबा रह जाए तो दर्पण अवतल होता है। यदि पैमाना दर्पण के बीच के भाग का स्पर्श करे तथा किनारों पर उठा रहे तो दर्पण उत्तल है।

(ii) प्रतिबिम्ब देखकर-किसी वस्तु को दर्पण से विभिन्न दूरियों पर रखने पर हर बार प्रतिबिम्ब वस्तु के बराबर ही बने तो दर्पण समतल है। यदि वस्तु को दर्पण के पास रखने पर प्रतिबिम्ब सीधा व बड़ा बने तो दर्पण अवतल है। यदि प्रतिबिम्ब प्रत्येक स्थिति में वस्तु से छोटा तथा सीधा बने तो दर्पण उत्तल है।

प्रश्न 5.
उत्तल दर्पण तथा अवतल दर्पण में अन्तर लिखिए। [RBSE 2011]
उत्तर –
| उत्तल दर्पण |
अवतल दर्पण |
| 1. इसमें परावर्तन करने वाला चमकीला तल बाहर की ओर उभरा होता है। |
1. इसमें परावर्तन करने वाला चमकीला तल अन्दर की ओर फँसा होता है। |
| 2. इसमें आभासी प्रति बिम्ब बनता है। |
2. इसमें वास्तविक एवं आभासी दोनों प्रकार के प्रतिबिम्ब बनते हैं। |
| 3. इसमें सीधा प्रतिबिम्ब बनता है। |
3. इसमें प्रतिबिम्ब उल्टा तथा सीधा दोनों बनते है। |
| 4. इसमें प्रतिबिम्ब छोटा बनता है। |
4. इसमें प्रतिबिम्ब बड़ा, छोटा तथा वस्तु के आकार का अर्थात् तीनों प्रकार का बनता है। |
प्रश्न 6.
(i) किसी गोलीय दर्पण के लिए आवर्धन का सूत्र लिखिए।
(ii) उस दर्पणं का नाम लिखिए, जो बिम्ब का सीधा तथा आवर्धित प्रतिबिम्ब बना सके।
(iii) उत्तल दर्पण के मुख्य फोकस की परिभाषा लिखिए। (RBSE 2016)
उत्तर-
(i) आवर्धन m = 
(ii) अवतल दर्पण
(iii) मुख्य अक्ष के समान्तर चलने वाली प्रकाश की किरणें, दर्पण से परावर्तन के पश्चात् मुख्य अक्ष पर मिलती हुई प्रतीत होती हैं, उसे उत्तल दर्पण का मुख्य फोकस कहते है|
प्रश्न 7.
एक उत्तल दर्पण के सामने 30 cm दूरी पर एक वस्तु पड़ी है। यदि इस दर्पण की फोकस दूरी 15 cm है तो वस्तु का जो प्रतिबिम्ब प्राप्त होता है उसकी चार विशेषताएँ लिखिए। (CBSE 2017)
उत्तर-
प्रतिबिम्ब की चार विशेषताएँ निम्न प्रकार हैं –
- प्रतिबिम्ब सीधा व आभासी होगा।
- प्रतिबिम्ब वस्तु से आकार में छोटा बनता है।
- प्रतिबिम्ब दर्पण के पीछे बनता है।
- प्रतिबिम्ब दर्पण के P व F बिन्दुओं के बीच बनता है।
प्रश्न 8.
ऐसी दोस्थितियों का वर्णन कीजिए जिन पर किसी बिम्ब को रखने पर, एक अवतल दर्पण दोनों बार बिम्ब का बड़ा प्रतिबिम्ब बनाता है। इन दोनों प्रतिबिम्बों के बीच दो अंतर लिखिए। (CBSE 2016)
उत्तर-
यह दो स्थितियाँ हैं –
- जब बिम्ब को अवतल दर्पण के सामने P व F बिन्दुओं के बीच रखते हैं।
- जब बिम्ब को अवतल दर्पण के सामने F व C बिन्दुओं के बीच रखते हैं।
दोनों प्रतिबिम्बों में अंतर निम्न प्रकार हैं –
| स्थिति (i) में, प्रतिबिम्ब दर्पण के पीछे बनता है। |
स्थिति (ii) में, प्रतिबिम्ब दर्पण के वक्रता केंद्र से दूर बनता है। |
| स्थिति (i) में, प्रतिबिम्ब सीधा व काल्पनिक होता है। |
स्थिति (ii) में, प्रतिबिम्ब उल्टा व वास्तविक बनता है। |
प्रश्न 9.
अवतल दर्पण द्वारा विभिन्न स्थितियों में रखी वस्तुओं की स्थिति, आकार और प्रकृति के लिए सारणी बनाइए।
उत्तर-
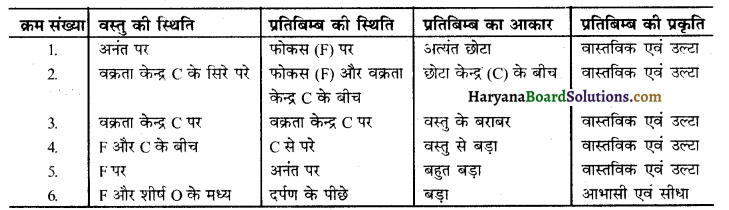
प्रश्न 10.
कोई बिम्ब 30 सेमी वक्रता त्रिज्या के अव तल दर्पण के सामने 12 सेमी दूरी पर स्थित है। दर्पण द्वारा बने प्रतिबिम्ब के चार अभिलक्षणों की सूची बनाइए। (CBSE 2017)
उत्तर-
- यह प्रतिबिम्ब आकार में बिम्ब से छोटा होगा।
- यह प्रतिबिम्ब आभासी भी होगा।
- यह प्रतिबिम्ब दर्पण के पीछे बनेगा।
- यह प्रतिबिम्ब सीधा बनेगा।
प्रश्न 11.
कोई बिम्ब 15 सेमी फोकस दूरी के उत्तल दर्पण के सामने 30 सेमी दूरी पर स्थित है। दर्पण द्वारा बने प्रतिबिम्ब के चार अभिलक्षणों का उल्लेख कीजिए। (CBSE 2017)
उत्तर-
- यह प्रतिबिम्ब आभासी होगा।
- यह हमेशा सीधा होगा।
- यह हमेशा बिम्ब से आकार में छोटा होगा।
- यह दर्पण के पीछे बनेगा।
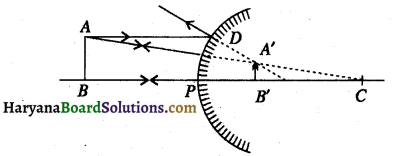
प्रश्न 12.
यदि किसी गोलीय दर्पण द्वारा उसके सामने रखे बिम्ब की किसी भी स्थिति के लिए सदैव ही बिम्ब का सीधा और आकार में छोटा प्रतिबिम्ब बनता है, तो यह दर्पण किस प्रकार का है? अपने उत्तर की पुष्टि के लिए नामांकित किरण आरेख खींचिए। (CBSE 2018)
उत्तर-
यह दर्पण एक उत्तल दर्पण है।
उत्तल दर्पण द्वारा किरण आरेख :
प्रश्न 13.
अपवर्तन के नियम लिखिए। (CBSE 2018,20)
उत्तर-
अपवर्तन के नियम निम्नलिखित हैं-
(i) किन्हीं दो माध्यमों के लिए एक ही रंग के प्रकाश के लिए आपतन कोण (i) की ज्या (sin) तथा अपवर्तन कोण (r) की ज्या (sin) का अनुपात सदैव स्थिरांक होता है।
\(\frac{\sin i}{\sin r}\) = स्थिरांक = 1n2
स्थिरांक 1n2 को पहले माध्यम का दूसरे के सापेक्ष अपवर्तनांक कहते हैं।
(ii) आपतित किरण, आपतन बिन्दु पर अभिलम्ब एवं अपवर्तित किरण तीनों एक ही तल पर होते हैं।
प्रश्न 14.
परावर्तन और अपवर्तन में क्या अन्तर हैं? बताइए।
उत्तर –
| परावर्तन |
अपवर्तन |
| 1. किसी चमकीली सतह से टकराकर प्रकाश की किरण का वापस लौट जाना प्रकाश का परावर्तन कहलाता है। |
1. पारदर्शक माध्यम से प्रकाश का एक-दूसरे पारदर्शक माध्यम में प्रवेश करने पर अपने पथ से विचलित हो जाना, प्रकाश का अपवर्तन कहलाता है। |
| 2. इसमें आपतन कोण तथा परावर्तन कोण सदा समान होते हैं। |
2. इसमें आपतन कोण और अपवर्तित कोण छोटे-बड़े होते हैं। |
| 3. परावर्तन के पश्चात् प्रकाश की किरणें पुन: उसी माध्यम में वापस लौट आती हैं। |
3. अपवर्तन के पश्चात् प्रकाश की किरणें दूसरे माध्यम में चली जाती हैं। |
प्रश्न 15.
जल से भरे किसी बर्तन की आभासी गहराई, उसकी वास्तविक गहराई से कम क्यों प्रतीत होती है?
उत्तर-
माना कि एक वस्तु O सघन माध्यम (जल) में रखी हुई है और देखने वाले की आँख विरल माध्यम (वायु) में वस्तु के ठीक ऊपर है। तब O से चलने वाली एक आपतित किरण OA जल तथा वायु के सीमा-पृष्ठ PQ पर अभिलम्बवत् गिरती है। इसके लिए आपतन कोण शून्य है। अतः अपवर्तन के नियमानुसार, अपवर्तन कोण भी शून्य होगा। अतः किरण सीधी AB दिशा में चली जाती है। दूसरी किरण OC, सीमा-पृष्ठ के बिन्दु C पर गिरती है। चूंकि किरण सघन माध्यम (जल) से विरल माध्यम (वायु) में जा रही है, अतः अपवर्तन के पश्चात् अभिलम्ब NCN’ से दूर हटती हुई दिशा CD में चली जाती है। अपवर्तित किरणें AB तथा CD पीछे बढ़ायी जाने पर बिन्दु I पर मिलती हैं।

इस प्रकार आँख को ये किरणें बिन्दु I से आती हुई प्रतीत होती हैं। अतः बिन्दु I, बिन्दु 0 का अपवर्तन द्वारा बना आभासी प्रतिबिम्ब है। चित्र में I, बिन्दु 0 की अपेक्षा ऊँचा है। अर्थात् जल से भरे बर्तन की आभासी गहराई, उसकी वास्तविक गहराई से कम प्रतीत होती है।
प्रश्न 16.
दिए गए किरण चित्र में आपतन कोण का मान एवं अपवर्तित किरण का नाम लिखिए। (RBSE 2015)
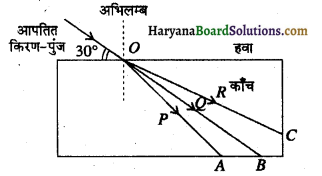
उत्तर-
आपतन कोण = 30°
अपवर्तित किरण – P
प्रश्न 17.
(a) काँच के स्लैब द्वारा प्रकाश के अपवर्तन को दर्शाने के लिए किरण आरेख खींचिए। इस आरेख पर अपवर्तन कोण तथा स्लैब से गुजरते समय प्रकाश किरण के पाश्विक विस्थापन को भी अंकित कीजिए।
(b) यदि वायु से कांच में गमन करते समय प्रकाश के लिए कांच का अपवर्तनांक 3/2 है, तो प्रकाश के कांच से वायु में गमन करने के लिए वायु का अपवर्तनांक ज्ञात कीजिए। (CBSE 2016)
उत्तर-
(a) .
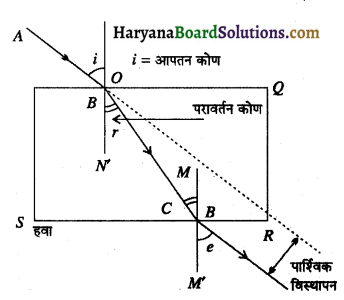
(b) जब वायु से कांच में गमन करते समय प्रकाश के लिए कांच का अपवर्तनांक 3/2 है तो प्रकाश के कांच से वायु में गमन करने के लिए वायु का अपवर्तनांक
ang=3/2
gna = \(\frac{1}{a^n g}=\frac{1}{(3 / 2)}=\frac{2}{3} \)
प्रश्न 18.
कोई छात्र किसी भली-भांति दूरस्थ बिम्ब के प्रतिबिम्ब को उत्तल लेंस द्वारा किसी पर्दे पर फोकसित करता है। तत्पश्चात् वह धीरे-धीरे बिम्ब को लेंस की ओर ले जाता है और हर बार वह लेंस को समायोजित करके बिम्ब के प्रतिबिम्ब को पर्दे पर फोकसित करता है।
(i) वह लेंस को किस दिशा में स्थानान्तरित करता है-पर्दे की ओर अथवा पर्दे से दूर?
(ii) प्रतिबिम्ब के आकार का क्या होता है-यह घटता है अथवा बढ़ता है?
(iii) जब वह बिम्ब को लेंस के अत्यधिक निकट ले जाता है तब पर्दे पर प्रतिबिम्ब कैसा होता है? (CBSE 2016)
उत्तर-
(i) वह लेंस को पर्दे से दूर स्थानान्तरित करता है।
(ii) प्रतिबिम्ब का आकार बढ़ता जाता है।
(iii) इस स्थिति में प्रतिबिम्ब अब पर्दे पर नहीं बनता क्योंकि अब प्रतिबिम्ब आभासी होता है।

प्रश्न 19.
उत्तल लेंस द्वारा क्रमशः तथा 2f की दूरी पर रखी वस्तु के लेंस द्वारा बने प्रतिबिम्बों की स्थिति, आकार, प्रकृति बताइए।
उत्तर-
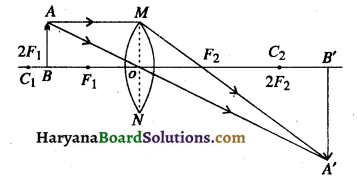
(i) जब वस्तु फोकस पर रखी हो-जब वस्तु फोकस F1 पर रखी हो तो वस्तु का प्रतिबिम्ब लेंस के दूसरी ओर अनन्त पर वास्तविक, वस्तु से बड़ा तथा उल्टा बनता है।
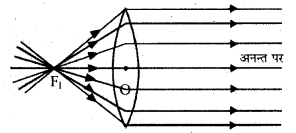
(ii) जब वस्तु लेंस के फोकस तथा फोकस दूरी की दूरी के बीच स्थित हो-चित्र में AB वस्तु लेंस के फोकस F तथा उसकी फोकस दूरी की दो गुनी दूरी 2F के बीच स्थित है। प्रतिबिम्ब 2F और अनन्त के बीच लेंस के दूसरी ओर बनता है।
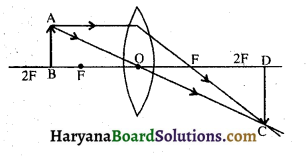
यह प्रतिबिम्ब वास्तविक उल्टा तथा वस्तु से बड़ा बनता है।
प्रश्न 20.
उत्तल लेंस तथा अवतल लेंस की पहचान कैसे करोगे?
उत्तर –
| उत्तल लेंस |
अवतल लेंस |
| 1. यह लेंस बीच में मोटा तथा किनारों पर पतला होता है। |
1. यह लेंस बीच में से पतला तथा किनारों पर मोटा होता है। |
| 2. यह प्रकाश किरणों को एक बिन्दु पर केन्द्रित करता है। |
2. यह प्रकाश पुंज को बिखेर देता है। |
| 3. वस्तु का प्रतिबिम्ब वास्त- विक, आभासी तथा उल्टा बनता है। |
3. वस्तु का प्रतिबिम्ब आभासी तथा सीधा बनता है। |
| 4. इसे बायीं ओर हिलाने पर प्रतिबिम्ब दायीं ओर गति करता है। |
4. इसे बायीं ओर हिलाने पर प्रतिबिम्ब भी बायीं ओर गति करता है। |
प्रश्न 21.
लेंस पर आपतित होने के पश्चात् प्रकाश किरण का अपवर्तन किस प्रकार होता है? समझाइए।
उत्तर-
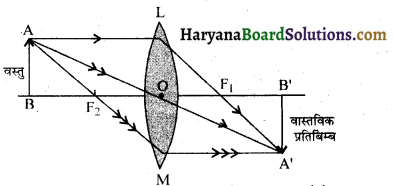
लेंस द्वारा बने प्रतिबिम्ब की स्थिति निम्नलिखित किरणों द्वारा ज्ञात की जाती है
- मुख्य अक्ष के समान्तर आ रही किरण अपवर्तन के पश्चात् लेंस के मुख्य फोकस से होकर जाती है।
- प्रकाशीय केन्द्र से गुजरने वाली किरण अपने मार्ग से हटे बिना सीधी चली जाती है।
- मुख्य फोकस से गुजरने वाली किरण अपवर्तन के पश्चात् मुख्य अक्ष के समान्तर चली जाती है।
प्रश्न 22.
किसी लेंस की क्षमता से क्या तात्पर्य है? इसका SI मात्रक लिखिए। कोई छात्र 40 सेमी फोकस दूरी का लेंस उपयोग कर रहा है तथा कोई अन्य छात्र-20 सेमी फोकस दूरी का लेंस उपयोग कर रहा है। इन दोनों लेंसों की प्रकृति और क्षमता लिखिए। (CBSE 2018)
उत्तर-
लेंस की क्षमता-किसी लेंस की फोकस दूरी के व्युत्क्रमानुपात को उस लेंस की क्षमता कहते हैं।
P (लेंस की क्षमता) =\(\frac{1}{f}\)
इसका S.I. मात्रक डाइऑप्टर (D) है।
(i) लेंस की फोकस दूरी (f) = 40 cm = 0.4 m
इस लेंस की क्षमता (P) = \(\frac{1}{0.4}=\frac{10}{4}\) = + 2.5 D
प्रकृति-यह एक उत्तल लेंस है क्योंकि उत्तल लेंस की क्षमता धनात्मक (Positive) होती है।
(ii) इस लेंस की फोकस दूरी (f) = – 20 cm = -0.2 m
इस लेंस की क्षमता (P) = \(\frac{1}{-0.2}=\frac{-10}{4}\) = – 5.0 D
प्रकृति-यह एक अवतल लेंस है क्योंकि अवतल लेंस की क्षमता ऋणात्मक (Negative) होती है।
प्रश्न 23.
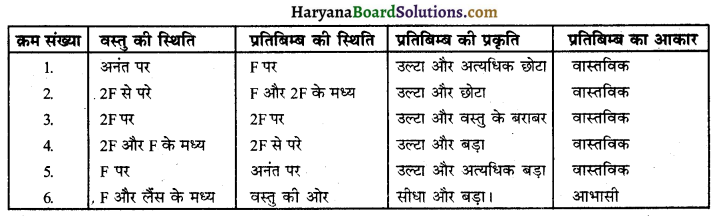
उत्तल लैंस द्वारा विभिन्न स्थितियों में रखी वस्तुओं के प्रतिबिम्ब की स्थिति, आकार और प्रकृति के लिए सारणी बनाइये।
उत्तर –
प्रश्न 24.
4.0 सेमी ऊँचाई का कोई बिम्ब 20 सेमी फोकस दूरी के किसी उत्तल लेंस के प्रकाशिक केन्द्र ‘O’ से 30 सेमी दूरी पर स्थित है। बनने वाले प्रतिबिम्ब की स्थिति और आकार ज्ञात करने के लिए किरण आरेख खींचिए। इस आरेख में प्रकाशिक केन्द्र ‘O’ तथा मुख्य फोकस ‘F’ अंकित कीजिए। प्रतिबिम्ब की ऊँचाई का लगभग अनुपात भी ज्ञात कीजिए। (CBSE 2018)
उत्तर-
u= – 30,f= 20 सेमी, h = 4 सेमी
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
⇒ \(\frac{1}{v}-\frac{1}{(-30)}=\frac{1}{20}\)
⇒ \(\frac{1}{v}=\frac{1}{60}\)
⇒ v = 60 सेमी
m= \(\frac{v}{u}=\frac{h_i}{h_0}\) =-2= \(\frac{h_i}{4} \)
⇒ h1 = – 8 सेमी
अतः m = \(\frac{\mathrm{H}_{\text {प्रतिबिम्ब }}}{{ }^{H_{\text {विम्ब }}}}=\frac{8}{4}\) = 2:1
दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
आपतित किरण, परावर्तित किरण, आपतन कोण, परावर्तन कोण तथा अभिलम्ब की परिभाषा लिखिए।
उत्तर-
(i) आपतित किरण-किसी दर्पण पर आकर आपतित होने वाली किरण. को आपतित किरण कहते हैं।
(ii) परावर्तित किरण-दर्पण पर टकराकर लौटने वाली प्रकाश किरण को परावर्तित किरण कहते हैं।
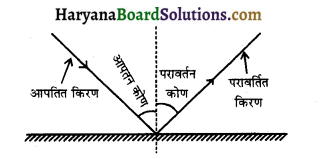
(ii) अभिलम्ब-जिस बिन्दु पर आपतित एवं परावर्तित किरणें मिलती हैं, उस बिन्दु पर खींचा गया लम्ब अभिलम्ब कहलाता है।
(iv) आपतन कोण-आपतित किरण तथा अभिलम्ब के बीच बने कोण को आपतन कोण कहते हैं।
(v) परावर्तन कोण-परावर्तित किरण तथा अभिलम्ब के बीच बने कोण को परावर्तन कोण कहते हैं।
प्रश्न 2.
जब अनंत से अवतल दर्पण की ओर किसी वस्तु को बढ़ाया जाए तो बिम्बों की स्थिति और उनकी प्रकृति स्पष्ट कीजिए।
उत्तर-
(i) वस्तु अनंत पर-जब कोई वस्तु अनंत पर होती है तो उसका वास्तविक बिम्ब F पर बनता है। किरण मख्य अक्ष के समान्तर चल कर दर्पण से टकराकर परावर्तित होती है तथा फोकस F पर मिलती है। इस स्थिति में बिम्ब अति छोटा, वास्तविक और उल्टा बनता है।
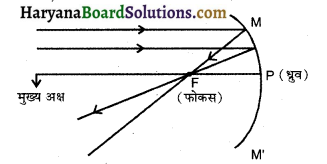
(ii) वस्तु अनंत व C के मध्य होने पर-वस्तु के C व अनंत के मध्य होने पर इसका वस्तु से छोटा, उल्टा एवं वास्तविक प्रतिबिम्ब F व C के बीच बनता है।
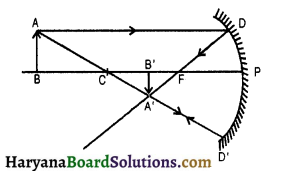
(iii) जब वस्तु C पर हो-वस्तु के C पर होने पर वस्तु का प्रतिबिम्ब वास्तविक, उल्टा एवं समान आकार का बनता है।
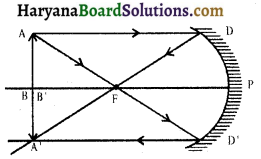
(iv) वस्तु F वC के बीच स्थित हो-जब वस्तु F व C के बीच हो तब AD मुख्य अक्ष के समांतर चलकर फोकस से गुज़रेगी तथा द्वितीय किरण की सहायता से वह वास्तविक, आवर्धित तथा उल्टा प्रतिबिम्ब बनाती है।
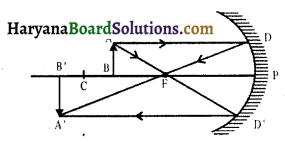
(v) वस्तु F पर स्थित हो-जब वस्तु फोकस पर स्थित हो तो मुख्य अक्ष के समान्तर चलने वाली किरण AD फोकस से गुजरेगी। दूसरी प्रकाशीय किरण की सहायता से , वह बहुत बड़ा, उल्टा और अनंत पर प्रतिबिम्ब बनाएगी।
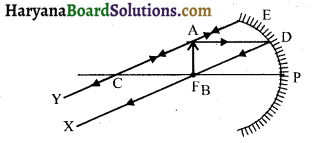
(vi) जब वस्तु P व F के बीच हो-जब कोई वस्तु P और F के बीच में हो तो किरण AD मुख्य अक्ष के समान्तर चलकर F से गुजरेगी तथा एक अन्य किरण E से टकराकर आभासी, सीधा और बड़ा बिम्ब बनाएगी।
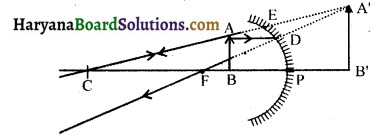

प्रश्न 3.
गोलीय दर्पण किसे कहते हैं ? ये कितने प्रकार के होते हैं? प्रत्येक के उपयोग लिखिए।
उत्तर-
गोलीय दर्पण (Spherical mirror)-गोलीय दर्पण किसी काँच के खोखले गोले के वे भाग होते हैं, जिनका एक तल पॉलिश किया हुआ होता है और दूसरा तल चमकदार होता है। चमकदार तल से प्रकाश का परावर्तन होता है।
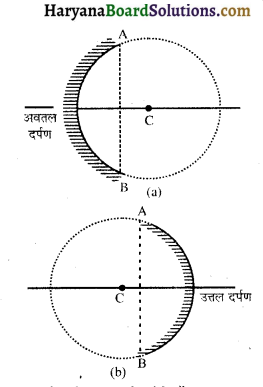
गोलीय दर्पण दो प्रकार के होते हैं-
(i) अवतल दर्पण (Concave mirror) तथा
(ii) उत्तल दर्पण (Convex mirror)।
(i) अवतल दर्पण (Concave mirror) इस दर्पण में उत्तल पृष्ठ (उभरे हुए पृष्ठ) पर चाँदी की पॉलिश की जाती है तथा प्रकाश का परावर्तन अवतल तल से होता है।
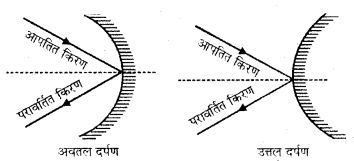
(ii) उत्तल दर्पण (Convex mirror)-इस दर्पण से अवतल पृष्ठ (दबे हुए पृष्ठ) पर चाँदी की पॉलिश की जाती है तथा प्रकाश का परावर्तन उत्तल तल से होता है।
गोलीय दर्पण के उपयोग (Uses of Spherical Mirror)-
अवतल दर्पण के उपयोग (Uses of concave mirror) –
- फोकस और ध्रुव के बीच रखी वस्तु का सीधा व बड़ा प्रतिबिम्ब बनने के कारण इस दर्पण को दाढ़ी बनाने के समय प्रयोग किया जाता है।
- कान, नाक व गले की जाँच करने के लिए डॉक्टरों द्वारा प्रयोग किया जाता है।
- परावर्तक के रूप में इसका प्रयोग किया जाता है।
- परावर्तक दूरदर्शी में इसका प्रयोग किया जाता है।
उत्तल दर्पण के उपयोग (Uses of convex mirror)
(i) इस दर्पण द्वारा अधिक विस्तृत क्षेत्र का प्रतिबिम्ब कम स्थान में बनने के कारण इसे ट्रक चालक के पार्श्व में लगा दिया जाता है, जिससे पीछे की ओर के काफी क्षेत्र का स्पष्ट व सीधा प्रतिबिम्ब दिखायी पड़ता है। इस दर्पण का दृष्टि क्षेत्र विस्तृत होता है।
(ii) सड़क पर लगे लैम्पों के परावर्तक तल के रूप में इस दर्पण का प्रयोग करने से प्रकाश अधिक बड़े क्षेत्र में फैल जाता. है।
प्रश्न 4.
12 सेमी फोकस दूरी के अवतल दर्पण द्वारा किसी बिम्ब का सीधा प्रतिबिम्ब बनाने के लिए कहा गया है।
(i) दर्पण के सामने बिम्ब की दूरी का क्या परिसर होना चाहिए?
(ii) बनने वाला प्रतिबिम्ब आकार में बिम्ब से छोटा होगा अथवा बड़ा? इस प्रकरण में प्रतिबिम्ब बनना दर्शाने के लिए किरण आरेख खींचिए।
(ii) इस बिम्ब का प्रतिबिम्ब कहाँ बनेगा, यदि इसे दर्पण के सामने 24 सेमी दूरी पर रख दिया जाए? अपने उत्तर की पुष्टि के लिए इस स्थिति के लिए भी किरण आरेख खींचिए।
उपरोद किरण आरेखों में ध्रुव, मुख्य फोकस और वक्रता केन्द्र की स्थितियों को भी दर्शाइए। (CBSE 2016)
उत्तर-
(i) अवतल दर्पण में किसी भी बिम्ब का सीधा प्रतिबिम्ब प्राप्त होगा यदि बिम्ब को दर्पण के ध्रुव तथा फोकस के मध्य रखा जाए।
फोकस, f= 12 सेमी
बिम्ब की दूरी का परिसर ‘P’ बिन्दु व ‘F’ बिन्दु के बीच होना चाहिए अर्थात् बिम्ब की दूरी 0 सेमी < 12 सेमी के मध्य होनी चाहिए।
(ii) बनने वाला प्रतिबिम्ब आकार में बिम्ब से बड़ा तथा सीधा बनेगा।
किरण आरेख :
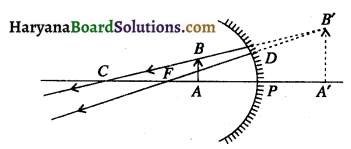
(iii) इस अवस्था में प्रतिबिम्ब भी दर्पण के सामने 24 सेमी पर बनेगा। इस दूरी पर प्रतिबिम्ब, बिम्ब के ठीक नीचे उल्टा बनेगा। इस प्रतिबिम्ब का img
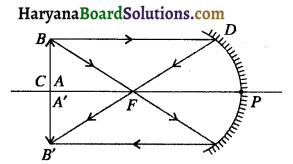
प्रश्न 5.
(a) प्रकाश किरण आरेखों की रचना करते समय हम ऐसी दो किरणों को चुनते हैं, जिनकी दर्पण से परावर्तन के पश्चात् की दिशा ज्ञात करना सरल होता है। ऐसी दो किरणों की सूची बनाइए और अवतल दर्पण के प्रकरण में परावर्तन के पश्चात् इन किरणों के पथों का उल्लेख कीजिए। इन्हीं दो किरणों का उपयोग अवतल दर्पण के ध्रुव और फोकस के बीच स्थित किसी बिम्ब के प्रतिबिम्ब की स्थिति, प्रकाश किरण आरेख खींचकर ज्ञात कीजिए।
(b) कोई अवतल दर्पण अपने सामने 20 सेमी दूरी पर स्थित किसी बिम्ब का तीन गुना आवर्धित प्रतिबिम्ब पर्दे पर बनता है। पर्दा बिम्ब से कितनी दूरी पर है? (CBSE 2017)
उत्तर-
(a)
(1) जब आपतित किरण मुख्य अक्ष के समानांतर होती है तो अपवर्तित किरण अवतल दर्पण के फोकस से होकर गुजरती है।
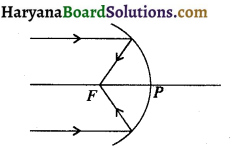
(2) जब आपतित किरण अवतल दर्पण के फोकस से गुजरती है तो अपवर्तित किरण दर्पण के मुख्य अक्ष के समानान्तर होती है।
(b) u=-20 cm, m = -3
m = –\(\left(\frac{v}{u}\right)\)
-3 = –\(\left(\frac{v}{-20}\right)\)
3x-20 = v
v= -60 सेमी
पर्दे की बिम्ब से दूरी = v-u = 60 – 20 =-40 सेमी
प्रश्न 6.
(a) यदि किसी दर्पण द्वारा उसके सामने स्थित बिम्ब का किसी भी स्थिति के लिए सदैव ही छोटा, सीधा और आभासी प्रतिबिम्ब बनता है, तो इस दर्पण की प्रकृति लिखिए और अपने उत्तर की पुष्टि के लिए किरण आरेख भी खींचिए। इस प्रकार के दर्पणों का एक उपयोग लिखिए तथा इनका उपयोग क्यों किया जाता है, उसका उल्लेख कीजिए।
(b) गोलीय दर्पणों की वक्रता त्रिज्या की परिभाषा लिखिए। किसी गोलीय दर्पण की प्रकृति और फोकस दूरी ज्ञात कीजिए, जिसकी वक्रता त्रिज्या + 24 सेमी है। (CBSE 2017)
उत्तर-
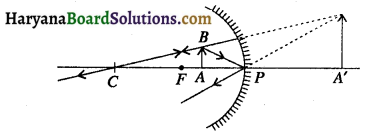
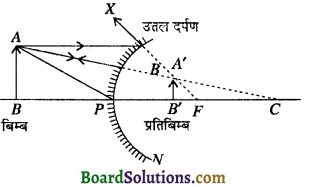
(a) यदि किसी दर्पण द्वारा उसके सामने स्थित बिम्ब का किसी भी स्थिति के लिए सदैव ही छोटा, सीधा और आभासी प्रतिबिम्ब बनता है तो वह दर्पण उत्तल है। इस तरह के दर्पणों का उपयोग सामान्यतः वाहनों के पश्च-दृश्य दर्पणों के रूप में किया जाता है। इनमें ड्राइवर अपने पीछे के वाहनों को देख सकते हैं जिससे वे सुरक्षित रूप से वाहन चला सकें
रेखाचित्र
बिम्ब की स्थिति :- अनंत तथा दर्पण के ध्रुव P के बीच
प्रतिबिम्ब की स्थिति – P तथा F के बीच दर्पण के पीछे
प्रतिबिम्ब की प्रकृति = आभासी, सीधा तथा छोटा।
(b) गोलीय दर्पण के ध्रुव से वक्रता केन्द्र तक की दूरी वक्रता त्रिज्या कहलाती है। गोलीय दर्पण का परावर्तक पृष्ठ जिस गोले का भाग है, उसकी त्रिज्या दर्पण की वक्रता त्रिज्या कहलाती है। अगर किसी दर्पण की वक्रता त्रिज्या 24 सेमी है, तो उसकी फोकस दूरी R/2 होगी।
f= \(\frac{24}{2}\) = +12 cm, यह दर्पण एक उत्तल दर्पण है।
प्रश्न 7.
सिद्ध कीजिए कि वायु के सापेक्ष काँच का अपवर्तनांक, काँच के सापेक्ष वायु के अपवर्तनांक का व्युत्क्रम होता है। अथवा प्रकाश-किरणों की उत्क्रमणीयता को स्पष्ट कीजिए।
उत्तर-
माना कि वायु में चलती एक प्रकाश-किरण OA एक काँच के गुटके PQRS पर गिरती है। यह किरण तल PQ पर अपवर्तित होकर काँच में AB दिशा में चली जाती है। इस प्रकार वायु में आपतित किरण OA है तथा काँच में अपवर्तित किरण AB है। यदि वायु में आपतन कोण i तथा काँच में अपवर्तन कोण । हो, तो वायु के सापेक्ष काँच का अपवर्तनांक
ang = \(\frac{\sin i}{\sin r}\) …………………… (i)
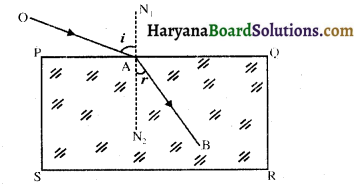
इसके विपरीत, यदि काँच के भीतर प्रकाश-किरण BA दिशा में चले तब वह तल PQ पर अपवर्तित होकर वायु में AO दिशा में जाएगी। इस स्थिति में काँच में आपतन कोण r होगा तथा वायु में अपवर्तन कोण i होगा। अतः जब प्रकाश-किरण काँच से वायु में जाती है तो काँच के सापेक्ष वायु का अपवर्तनांक
gna = \(\frac{\sin r}{\sin i}\) ……………………….. (ii)
समीकरण (i) एवं (ii) की तुलना करने पर,
ang= \(\frac{1}{{ }_g n_a} \)
अर्थात् वायु के सापेक्ष काँच का अपवर्तनांक, काँच के सापेक्ष वायु के अपवर्तनांक का व्युत्क्रम होता है। यदि वायु के सापेक्ष काँच का अपवर्तनांक \(\frac{3}{2}\) है, तो काँच के सापेक्ष वायु का अपवर्तनांक \(\frac{2}{3}\) होगा।

प्रश्न 8.
पार्श्व विस्थापन से क्या तात्पर्य है? सिद्ध कीजिये कि दो समान्तर पृष्ठों वाले काँच के गुटके से निकलने वाली किरण आपतित किरण के समान्तर होती (CBSE 2020)
उत्तर-
पार्श्व विस्थापन (Lateral Displacement)जब कोई प्रकाश-किरण समान्तर पृष्ठों वाले काँच के गुटके पर गिरती है तो अपवर्तन के पश्चात् गुटके के दूसरे पृष्ट से बाहर निकलने पर उसकी दिशा में कोई अन्तर नहीं पड़ता, परन्तु उसके मार्ग में कुछ विस्थापन आ जाता है। इसे ‘पार्श्व विस्थापन’ कहते हैं।
माना कि कोई प्रकाश-किरण OA एक काँच के गुटके PQRS पर आपतन कोण i बनाती हुई गिरती है। गुटके के पहले पृष्ठ PQ पर अपवर्तन के पश्चात् यह किरण अभिलम्ब की ओर झुक जाती है तथा इसकी दिशा AB हो जाती है। माना कि अपवर्तन कोण r है। चूँकि गुटके के दोनों पृष्ठ समान्तर हैं, अतः किरण AB गुटके के दूसरे पृष्ठ SR पर आपतन कोण बनाती हुई गिरती है तथा अपवर्तन के पश्चात् अभिलम्ब से दूर हट जाती है। माना वायु में निकलने पर निर्गत किरण BC, अभिलम्ब से निर्गत कोण e बनाती है।
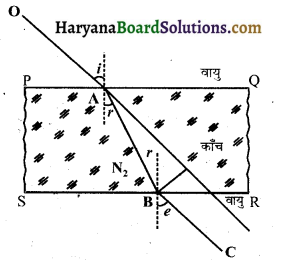
पृष्ठ PQ पर प्रकाश-किरण वायु से काँच में जा रही है। अत: वायु के सापेक्ष काँच का अपवर्तनांक
ang = \(\frac{\sin i}{\sin r}\) ………………….. (i)
पृष्ठ SR पर किरण काँच से वायु में जा रही है। अतः काँच के सापेक्ष वायु का अपवर्तनांक
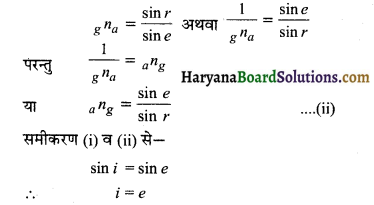
अतः स्पष्ट है कि दो समान्तर पृष्ठों वाले काँच के गुटके से निकलने वाली किरण आपतित किरण के समान्तर होती है।
प्रश्न 9.
(a) किसी अवतल लेंस द्वारा उसके सामने रखे किसी बिम्ब का प्रतिबिम्ब बनना दर्शाने के लिए किरण आरेख खींचिए।
(b) उपर्युक्त आरेख में बिम्ब-दूरी, प्रतिबिम्ब दूरी को इनके उचित चिह्न (नई कार्तीय चिह्न परिपाटी के अनुसार धनात्मक (+) अथवा ऋणात्मक (-) सहित दर्शाइए और उल्लेख कीजिए कि इस प्रकरण में ये दूरियाँ अवतल लेंस की फोकस दूरी () से किस प्रकार संबंधित हैं।
(c) उस लेंस की प्रकृति और क्षमता ज्ञात कीजिए, जो अपने प्रकाशिक केन्द्र से 40 सेमी दूरी पर स्थित किसी बिम्ब का -1 आवर्धन का प्रतिबिम्ब बनाता है। (CBSE 2016)
उत्तर-
(a)
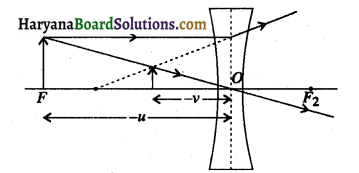
(b) बिम्ब दूरी (u) = – u
प्रतिबिम्ब की दूरी (v) = – v
फोकस दूरी (f) =-f
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
(c) दिया गया है – m = – 1, u = – 40 सेमी
m = \(\frac{v}{u}\)
⇒ -1 = \(\frac{v}{-40}\)
v = 40 सेमी
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
= \(\frac{1}{40}-\frac{1}{-40} \)
f = 20 सेमी = 0.2 मी.
P= \(\frac{1}{f}=\frac{1}{0.20}\) =5D
यह लेंस एक उत्तल लेंस हैं, क्योंकि उत्तल लेंस वास्तविक और उल्टा प्रतिबिम्ब बनाता है।
प्रश्न 10.
उत्तल लेंस के प्रकरण में बिम्ब दरी (u) के साथ प्रतिबिम्ब दूरी (v) में विचरण को दर्शाने वाली नीचे दी गयी प्रेक्षण तालिका का विश्लेषण कीजिए और परिकलन किए बिना ही निम्नलिखित प्रश्नों के उत्तर दीजिए :
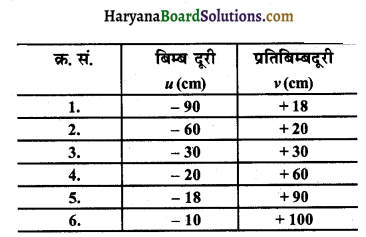
(a) उत्तल लेंस की फोकस दूरी क्या है? अपने उत्तर की पुष्टि के लिए कारण लिखिए।
(b) उस प्रेक्षण की क्रम संख्या लिखिए जो सही नहीं है। यह निष्कर्ष आपने किस आधार पर निकाला है?
(c) कोई भी उचित पैमाना लेकर प्रेक्षण संख्या 4 के लिए प्रकाश किरण आरेख खींचिए और आवर्धन का लगभग मान ज्ञात कीजिए। (CBSE 2017)
उत्तर-
(a) क्रम संख्या 3 से हमें यह ज्ञात होता है कि लेंस की त्रिज्या 30 cm है क्योंकि जब उत्तल लेंस में बिम्ब c पर रखा जाता है तो लैंस से बिम्ब और प्रतिबिम्ब की दूरी समान होती है। फोकस दूरी हमेशा त्रिज्या की आधी होती है तो इस लेंस की फोकस दूरी + 15 cm होगी।
(b) संख्या 6 सही नहीं है क्योंकि बिम्ब की दूरी F और P के बीच है। इस तरह की स्थिति के लिए प्रतिबिम्ब हमेशा आभासी होता है, लेकिन इस स्थिति में प्रतिबिम्ब वास्तविक है, क्योकि प्रतिबिम्ब की दूरी धनात्मक हैं।
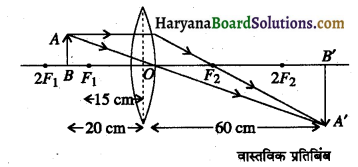
m = \(\frac{v}{u} \)
v = +60 cm
u = -20 cm
m = \(\left(\frac{60}{-20}\right)\) =-3
प्रश्न 11.
निम्नलिखित प्रेक्षण सारणी का विश्लेषण कीजिए जिसमें उत्तल लेंस की स्थिति में बिम्ब दूरी (u) के साथ प्रतिबिम्ब दूरी (v) का विचरण दर्शाया गया है, और बिना कोई परिकलन किए ही निम्नलिखित प्रश्नों के उत्तर दीजिए :
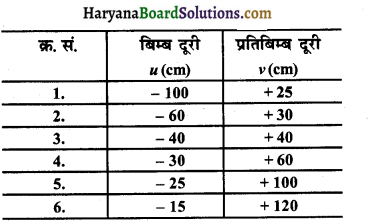
(a) उत्तल लेंस की फोकस दूरी क्या है? अपने उत्तर की पुष्टि के लिए कारण दीजिए।
(b) उस प्रेक्षण की क्रम संख्या लिखिए जो सही नहीं है। यह निष्कर्ष आपने किस आधार पर निकाला है।
(c) किसी उचित पैमाने को चुनकर क्रम संख्या 2 के प्रेक्षण के लिए किरण आरेख खींचिए। आवर्धन का लगभग मान भी ज्ञात कीजिए। (CBSE 2017)
उत्तर-
(a) इस उत्तल लेंस की फोकस दूरी + 20 cm होगी, क्योंकि इस सारणी में तीसरी क्रम संख्या में बिम्ब और प्रतिबिम्ब दूरी समान है, तो हमें यह ज्ञात होता है कि R = 40
फोकस दूरी हमेशा इसकी आधी होती है इसलिए फोकस दूरी + 20 cm होगी।
(b) क्रम संख्या 6 सही नहीं है क्योंकि u =- 15 cm और इस केस में प्रतिबिम्ब आभासी बनता है न कि वास्तविक।
(c) 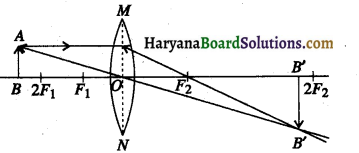
आवर्धन का लगभग मान
m = \( \begin{aligned}&\frac{v}{u} \\= &\frac{30}{-60}=-\frac{1}{2}=\end{aligned}\) = -0.5
प्रश्न 12.
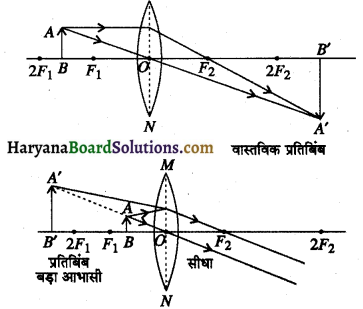
अवतल लैंस द्वारा किसी वस्तु का निम्न स्थितियों में बना प्रतिबिम्ब कैसा होगा ? किरण आरेख भी बनाइए।
(a) जब वस्तु अनन्त पर हो।
(b) जब वस्तु 2F तथा F1 के मध्य हो।
उत्तर-
(a) जब वस्तु अनन्त पर हो-अनन्त से आने वाली मुख्य अक्ष के समान्तर किरणे अपवर्तन के पश्चात् अपसारित हो (फैल) जाती हैं तथा फोकस F1 से निकलती प्रतीत होती हैं अतः प्रतिबिम्ब सीधा, आभासी व अत्यधिक छोटा फोकस F1 पर बनता है।
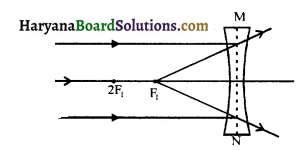
(b) जब वस्तु 2F व F1 के मध्य हो-वस्तु का प्रतिबिम्ब आभासी, सीधा, छोटा तथा फोकस F1 तथा प्रकाशिक केन्द्र के बीच बनता है।
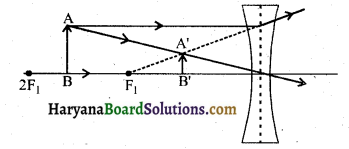
आकिक प्रश्न (Numerical Questions)
उत्तल दर्पण पर आधारित प्रश्न (Problems on Based Convex Mirror)
विशेष तथ्य-
1. उत्तल दर्पण के प्रश्नों को हल करने के लिये चि परिपाटी
f= + (धनात्मक) तथा 0 = + (वस्तु का आकार)
v=+ (धनात्मक) I = + (प्रतिबिम्ब का आकार)
u= – (ऋणात्मक)
m = + (धनात्मक) सदैव 1 से छोटा
2. अज्ञात राशि का चिन्ह प्रश्न के हल करने में नहीं लिया जाता है वह प्रश्न हल करने के पश्चात् स्वयं निकल कर आता है।
प्रश्न 1.
25 सेमी फोकस दूरी के उत्तल दर्पण की वक्रता त्रिज्या ज्ञात कीजिए।
हल : प्रश्नानुसार, फोकस दूरी f= 25 सेमी
वक्रता. त्रिज्या R = ?
∴ वक्रता त्रिज्या R=2f
= 2 x 25
R=50 सेमी
प्रश्न 2.
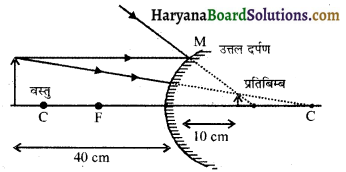
उत्तल दर्पण से 40 cm दूर रखी वस्तु का प्रतिबिम्ब 10 cm दूर बनता है। उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए तथा सम्बन्धित किरण आरेख भी बनाइए।
हल : वस्तु से दर्पण की दूरी u = – 40 cm
प्रतिबिम्ब की दर्पण से दूरी v = 10 cm
माना दर्पण की फोकस दूरी f है, अतः
\(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
\( =\frac{1}{-40}+\frac{1}{10}\)
\(=\frac{-1+4}{40}=\frac{3}{40}\)
∴ फोकस दूरी f = \(\frac{40}{3}\) =13.3 cm
प्रश्न 3.
एक उत्तल दर्पण की फोकस दूरी 20 cm है। इस दर्पण से 25 cm दूर रखी वस्तु के प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
हल :
प्रश्नानुसार, उत्तल दर्पण की फोकस दूरी (f) = 20 cm
वस्तु की दर्पण से दूरी (u) = – 25 cm
दर्पण से प्रतिबिम्ब की दूरी (v) = ?
∵ \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
∴ \(\frac{1}{-25}+\frac{1}{v}=\frac{1}{20}\)
\(\frac{1}{v}=\frac{1}{20}+\frac{1}{25}=\frac{5+4}{100}=\frac{9}{100}\)
अतःv = \(\frac{100}{9} \) =+11.1cm
अतः प्रतिबिम्ब उत्तल दर्पण के पीछे 11.1 cm दूरी पर बनता है।

प्रश्न 4.
एक उत्तल दर्पण से 25 cm दूर रखी वस्तु का प्रतिबिम्ब वस्तु की लम्बाई का आधा बनता है। दर्पण की फोकस दूरी ज्ञात कीजिए।
हल : प्रश्नानुसार,
वस्तु की उत्तल दर्पण से दूरी u = – 25 cm
आवर्धन (m) = img

∴ फोकस दूरी f= 25 cm
प्रश्न 5.
6 cm लम्बाई की एक कील उत्तल दर्पण के सामने 20 cm दूर रखी है। यदि इस दर्पण की फोकस दूरी 10 cm हो तो कील के प्रतिबिम्ब की लम्बाई तथा स्थिति ज्ञात कीजिए।
हल :
प्रश्नानुसार,
वस्तु की लम्बाई h = 6 cm
कील की उत्तल दर्पण से दूरी = -20 cm
दर्पण की फोकस दूरी f= + 10cm
कील के प्रतिबिम्ब की लम्बाई v = ?
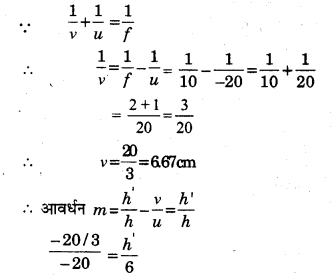
h’= 2 cm
अतः प्रतिबिम्ब दर्पण के पीछे 6.67 cm दूरी पर 2 cm लम्बाई का बनेगा।
अवतल दर्पण पर आधारित प्रश्न । (Problems Based on Concave Mirror)
विशेष तथ्य
1. अवतल दर्पण के लिये चि परिपाटी
f= – (ऋणात्मक)
u = – (ऋणात्मक)
v = – लेकिन जब u m = लेकिन जब u 2. अज्ञात राशि का चिन्ह नहीं लेते, वह स्वयं प्रश्न को हल करते समय निकलकर आता है।
प्रश्न 6.
एक अवतल दर्पण से 20 cm दूर रखी वस्तु का प्रतिबिम्ब 30 cm दूर बनता है। दर्पण की फोकस दूरी ज्ञात कीजिए।
हल :
प्रश्नानुसार, दर्पण से वस्तु की दूरी u = -20 cm
प्रतिबिम्ब की दूरी v = -30 cm
फोकस दूरी (f) = ?
∴ \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
= \(-\frac{1}{20}-\frac{1}{30}=\frac{-3-2}{60}=\frac{-5}{60}\)
‘या \(\frac{1}{f}=-\frac{1}{12}\) या f=-12cm
अतः अवतल दर्पण की फोकस दूरी 12 cm होगी।
प्रश्न 7.
एक अवतल दर्पण की फोकस दूरी 25 cm है। दर्पण से 20 cm की दूरी पर रखी वस्तु के प्रतिबिम्ब की स्थिति एवं प्रकृति बताइए।
हल : प्रश्नानुसार,
अवतल दर्पण की फोकस दूरी f= – 25 cm
अवतल दर्पण से वस्तु की दूरी u = – 20 cm
प्रतिबिम्ब की दर्पण से दूरी v = ?
∴ \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
∴ \(\frac{-1}{20}+\frac{1}{v}=-\frac{1}{25}\)
∴ \(\frac{1}{v}=-\frac{1}{25}+\frac{1}{20}=\frac{-4+5}{100}=\frac{1}{100}\)
∴ v= 100 cm
अतः प्रतिबिम्ब दर्पण से 100 cm की दूरी पर बनेगा।
आवर्धन (m) = \(-\frac{v}{u}=-\frac{100}{-(20)}\) = 5
अतः प्रतिबिम्ब दर्पण से 100 cm दूर, सीधा तथा वस्तु से 5 गुना बनता है। चूँकि प्रतिबिम्ब दर्पण के पीछे बनता है। अतः प्रतिबिम्ब आभासी है।
प्रश्न 8.
एक अवतल दर्पण की वक्रता त्रिज्या 60 cm है। 4 cm लम्बी एक वस्तु दर्पण से 45 cm दूर रखी है। प्रतिबिम्ब की स्थिति तथा लम्बाई ज्ञात कीजिए।
हल : प्रश्नानुसार ,
अवतल दर्पण की वक्रता त्रिज्या R = – 60 cm
वस्तु की लम्बाई (h) = 4 cm
वस्तु की दर्पण से दूरी u = – 45 cm
(i) अवतल दर्पण की फोकस दूरी f= – \(\frac{60}{2}\) =-30
∴ सूत्र \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\) से,
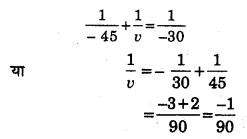
v=-90 cm
अतः प्रतिबिम्ब दर्पण से 90 cm दूर बनेगा।
(ii) माना प्रतिबिम्ब की लम्बाई h है
\(\frac{h^{\prime}}{h}=-\frac{v}{u} \)
\(\frac{h^{\prime}}{u}=-\frac{90}{-45} \)
\(\frac{h^{\prime}}{u}=-\frac{2}{1} \)
या h= – 8 cm
अतः प्रतिबिम्ब की लम्बाई 8 cm होगी।

प्रश्न 9.
12 cm फोकस दूरी वाले अवतल दर्पण के सामने 4 cm लम्बी वस्तु कहाँ रखी जाए कि उसका 1 cm लम्बा.प्रतिबिम्ब बने ?
हल :
प्रश्नानुसार, अवतल दर्पण की फोकस दूरी f= – 12 cm
वस्तु की लम्बाई h = 4 cm
प्रतिबिम्ब की लम्बाई h’ = 1 cm
माना वस्तु को u cm दूर रखा जाए।
अवतल दर्पण द्वारा बना प्रतिबिम्ब वस्तु से छोटा बन रहा है। इसलिए प्रतिबिम्ब उल्टा तथा वास्तविक होगा। अतः प्रतिबिम्ब की लम्बाई ऋणात्मक रखेंगे
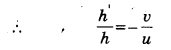

अतः अवतल दर्पण से वस्तु को 60 cm दूर रखा जाए।
प्रश्न 10.
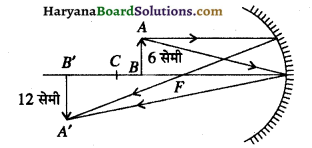
कोई 6 सेमी लम्बा बिम्ब 30 सेमी फोकस दूरी के अवतल दर्पण के मुख्य अक्ष के लम्बवत् स्थित है। दर्पण से बिम्ब की दूरी 45 सेमी है। दर्पण सूत्र का उपयोग करके बनने वाले प्रतिबिम्ब की स्थिति, प्रकृति और आकार निर्धारित कीजिए। इस प्रकरण में प्रतिबिम्ब बनना दर्शाने के लिए नामांकित किरण आरेख भी खींचिए।
अथवा
6 सेमी आकार का कोई बिम्ब 30 सेमी फोकस दूरी के किसी उत्तल लेंस के सामने 50 सेमी दूरी पर स्थित है। इस बिम्ब का तीक्ष्ण प्रतिबिम्ब प्राप्त करने के लिए पर्दै को लेंस से कितनी दूरी पर रखा जाना चाहिए? प्रतिबिम्ब की प्रकृति और आकार ज्ञात कीजिए। इस प्रकरण में प्रतिबिम्ब बनना दर्शाने के लिए नामांकित किरण आरेख भी खींचिए।
हल :
दिया है, बिम्ब की ऊँचाई h = 6 सेमी, फोकस दूरी f=-30 सेमी
बिम्ब की दूरी (दर्पण से) v = – 45 सेमी

अवतल दर्पण से बिम्ब की दूरी = – 90 सेमी। \
वस्तु का आकार = 6 सेमी,
प्रतिबिम्ब का आकार = ?
सूत्र आवर्धन m = –\(\frac{v}{u} \)
\(-\frac{90}{45}\) =-2
nc=-2 x 6 सेमी
= – 12 सेमी
प्रतिबिम्ब = वास्तविक, उल्टा एवं बड़ा होगा।
अथवा
दिया है, f= 30 सेमी, u = – 50 सेमी, h = 6.0 सेमी AM
प्रश्न 11.
किसी दर्पण द्वारा बना प्रतिबिम्ब, वास्तविक, उल्टा और -1 आवर्धन का है। यदि प्रतिबिम्ब की दर्पण से दूरी 40 cm है, तो बिम्ब कहाँ स्थित है? यदि बिम्ब को दर्पण की ओर 20 cm स्थानांतरित कर दिया जाए, तो प्रतिबिम्ब कहाँ बनेगा? अपने उत्तर की पुष्टि के लिए कारण दीजिए तथा बिम्ब की नई स्थिति के लिए किरण आरेख खींचिए। (CBSE 2016)
हल-
आवर्धन, m = – 1; प्रतिबिाय बास्तविक तथा उल्टा है; प्रतिबिम्ब की दूरी = – 40 cm
यह दर्पण अवतल है।
∵ प्रतिबिम्ब वास्तविक है।
\(\frac{-v}{u}=m \quad \Rightarrow \frac{-(-40)}{u}=-1\)
⇒ u = \(\frac{-(-40)}{-1}\)
⇒ u = -40 cm
∵ बिम्ब दर्पण के सामने 40 cm की दूरी पर स्थित है।
इस अवस्था में, बिम्ब और प्रतिबिम्ब दोनों दर्पण के सामने एक ही बिन्दु ‘C’ पर स्थिति है। जब बिम्ब को दर्पण की और 20 cm पर स्थानान्तरित किया जाता है तो वह दर्पण के ‘F’ बिन्दु पर स्थिति होगा। अब प्रतिबिम्ब दर्पण के सामने अनंत दूरी (Infinity) पर बनेगा।
दर्पण सूत्र द्वारा,
\(\frac{1}{f}=\frac{1}{v}=\frac{1}{u} \Rightarrow \frac{1}{f}=\frac{1}{-40}+\frac{1}{-40} \)
⇒\(\frac{1}{f}=\frac{-1}{40}-\frac{1}{40} \Rightarrow \frac{1}{f}=\frac{-2}{40}=\frac{-1}{20} \)
⇒ f=-20 cm
दूसरी स्थिति :f=-20 cm; u = -20 cm; v= ?
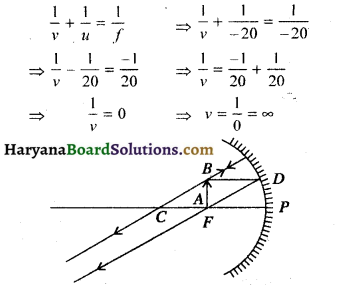
∴ अतः प्रतिबिम्ब दर्पण के सामने अनंत पर बनेगा।
प्रश्न 12.
कोई 3 cm ऊँचाई का बिम्ब 12 cm फोकस दूरी के किसी अवतल दर्पण के सामने 18 cm दूरी पर स्थित है। इस दर्पण से किसी पर्दे को कितनी दूरी पर रखा जाना चाहिए ताकि इस पर्दे पर बिम्ब का स्पष्ट प्रतिबिम्ब दिखाई दे। प्रतिबिम्ब की ऊँचाई भी परिकलित कीजिए। (CBSE 2017)
हल: f = -12
u = -18
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
\(\frac{1}{-12}=\frac{1}{v}+\frac{1}{-18}\)
\(\frac{1}{18}-\frac{1}{12}=\frac{1}{v} \)
\(\frac{2-3}{36}=\frac{1}{v} \)
v = -36 cm
m = \(\frac{-v}{u}=\frac{-(-36)}{-18}\)
m = -2

m = \(\frac{H_i}{3}\)
प्रतिबिम्ब की ऊँचाई = – 2 × 3
प्रतिबिम्ब की ऊँचाई = – 6 cm
प्रश्न 13.
किसी दर्पण से 30 cm दूरी पर स्थित मोमबत्ती की ज्वाला का प्रतिबिम्ब दर्पण के सामने उसके ध्रुव से 60 cm दूरी पर स्थित पर्दे पर बनता है। दर्पण की प्रकृति क्या है? इसकी फोकस दूरी ज्ञात कीजिए। यदि ज्वाला की ऊँचाई 2.4 cm है, तो इसके प्रतिबिम्ब की ऊँचाई ज्ञात कीजिए। उल्लेख कीजिए कि यह प्रतिबिम्ब सीधा होगा अथवा उल्टा। (CBSE 2017)
हल :
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
= \(\frac{1}{-60}+\frac{1}{-30}\)
\(\frac{1}{f}=\frac{-1-2}{60}\)
∴ f=-20
m = \(-\left(\frac{v}{u}\right)=-\left(\frac{-60}{-30}\right)\)
m =-2

प्रतिबिम्ब की ऊँचाई = 2 x (-2.4) =- 4.8 cm
यह एक अवतल दर्पण है। यह प्रतिबिम्ब उल्टा बनेगा।

प्रश्न 14.
4 cm आकार का कोई बिम्ब 15.0 फोकस दूरी के किसी अवतल दर्पण के सामने 25.0 cm दूरी पर स्थित है।
(i) इस दर्पण के सामने किसी पर्दे को कितनी दूरी पर रखा जाए ताकि उस पर बिम्ब का तीक्ष्ण प्रतिबिम्ब बने।
(ii) बनने वाले प्रतिबिम्ब का आकार ज्ञात कीजिए।
(ii) इस प्रकरण में प्रतिबिम्ब बनना दर्शाने के लिए किरण आरेख दीजिए। (CBSE 2020)
हल : दिया है, बिम्ब का आकार, h1 = 4 cm
u=-25 cm,f=- 15 cm,v= ?
(i) दर्पण सूत्र द्वारा,
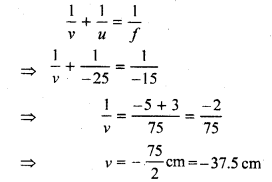
इसलिए इस प्रतिबिम्ब को प्राप्त करने के लिए पर्दे को दर्पण के सामने 37.5 cm दूरी पर रखना चाहिए।
(ii) प्रतिबिम्ब आकार (h2) = ?
\(\frac{h_2}{h_1}=\frac{-v}{u} \Rightarrow \frac{h_2}{4}=\frac{-\left(\frac{-75}{2}\right)}{-25}\)
∴ h2 = \(\frac{-75}{2 \times 25} \times 4\) = – 6cm
प्रतिबिम्ब का आकार 6 cm होगा, (-) चिन्ह दर्शाता है कि प्रतिबिम्ब उल्टा बनता है।
(iii)
विशेष तथ्य
1. उत्तल लेंस के लिये चिन्ह परिपाटी
f(फोकस दूरी) =+
u (वस्तु की दूरी) =
v (प्रतिबिम्ब की दूरी) = + लेकिन जब u O (वस्तु का आकार) =+ धनात्मक
प्रतिबिम्ब का आकार = – ऋणात्मक लेकिन जब m = – (ऋणात्मक) लेकिन जब u <fसे तब m = +
2. प्रश्न को हल करते समय अज्ञात राशि का चि नहीं रखते वह प्रश्न को हल करते समय स्वयं निकल कर आता है।
प्रश्न 15.
0.12 मीटर फोकस दूरी के उत्तल लेंस से वस्तु का 3 गुना वास्तविक प्रतिबिम्ब पर्दे पर प्राप्त करने के लिए वस्तु को लेंस से कितनी दूर रखना पड़ेगा?
हल : प्रश्नानुसार, उत्तल लेंस की फोकस दूरी,f= 0.12

माना वस्तु को उत्तल लेंस से 4 मीटर दूर रखा जाए।
m=\(\frac{u}{v}\) =-3
वास्तविक प्रतिबिम्ब के लिए आवर्धन क्षमता ऋणात्मक लेते हैं जो विशेष तथ्य में स्पष्ट है।
या \(\frac{v}{u}=-\frac{3}{1}\)
या v=-3u
सूत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
या \(\frac{1}{0.12}=\frac{1}{-3 u}-\frac{1}{u}\)
या \(\frac{1}{0.12}=\frac{-1-3}{3 u} \)
या \(\frac{1}{0.12}=-\frac{4}{3 u} \text { या } u=\frac{-0.12 \times 4}{3}=-0.16 \)
अतः वस्तु को लेंस से 0.16 मीटर दूर रखा जायेगा।
प्रश्न 16.
एक उत्तल लेंस से 15 cm दूर रखी वस्तु का चार गुना बड़ा वास्तविक प्रतिबिम्ब बनता है। उत्तल लेंस की फोकस दूरी ज्ञात कीजिए।
हल :
प्रश्नानुसार,
वस्तु की उत्तल लेंस से दूरी u = – 15 cm
आवर्धन (m)=-4
माना उत्तल लेंस की फोकस दूरी f cm है।
m = \(\frac{v}{u}\) = -4 ;
\(\frac{v}{-15}\) = -4
∴ v= 60 cm .
लेंस के सूत्र
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{f}=\frac{1}{60}-\frac{1}{-15}\)
\(\frac{1}{f}=\frac{1}{60}+\frac{1}{15}=\frac{5}{60}=\frac{1}{12}\)
f= 12 cm
अतः लेंस की फोकस दूरी 12 cm होगी।
प्रश्न 17.
(a) 10 cm फोकस दूरी के किसी उत्तल लेंस के आधे भाग को काले काग़ज से ढक दिया गया है। क्या यह लेंस 30 cm दूरी पर स्थित बिम्ब का पूरा प्रतिबिम्ब बना सकता है? अपने उत्तर की पुष्टि के लिए एक किरण आरेख खींचिए।
(b) कोई 4 cm लम्बा बिम्ब 20 cm फोकस दूरी के किसी उत्तल लेंस के मुख्य अक्ष के लम्बवत् रखा है। बिम्ब की लेंस से दूरी 15 cm है। प्रतिबिम्ब की प्रकृति, स्थिति और आकार ज्ञात कीजिए। [CBSE 2015]
हल:
(a) हाँ, क्योंकि बिम्ब से जाने वाली प्रकाश किरणों पर कोई प्रभाव नहीं पड़ता है, केवल बनने वाले प्रतिबिम्ब की तीव्रता कम हो जाती है।
(b) बिम्ब की लम्बाई (O) = + 4 सेमी.
लैन्स की फोकस दूरी (f) = 20 सेमी.
बिम्ब की लैंस से दूरी = (u) = -15 सेमी.
लैन्स सूत्र से-

आवर्धन के सूत्र m= \(\frac{\mathrm{I}}{\mathrm{O}}=\frac{v}{u}\) = “से.
\(\frac{I}{4}=\frac{-60}{-15}\)
∴ I =4×4= 16 सेमी
अतः प्रतिबिम्ब आभासी सीधा व वस्तु से बड़ा बनता है।
प्रश्न 18.
एक मोमबत्ती तथा पर्दे के बीच की दूरी 90 cm है। इसके मध्य 20 cm फोकस दूरी वाला उत्तल लेंस कहाँ रखा जाए कि मोमबत्ती का वास्तविक, उल्टा प्रतिबिम्ब पर्दे पर बने।
हल:
प्रश्नानुसार, u+y= 90 cm
माना वस्तु से लेंस की दूरी u = – x cm
अतः लेंस से प्रतिबिम्ब (पर्दै) की दूरी
v = (90-x) cm
अतः लेंस के सूत्र से –
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)

(x-60) (x-30) = 0
अतःx-60 = 0
∴ x = 60
अत: वस्तु की लेंस से दूरी 60 cm होगी।
प्रतिबिम्ब पर्दे की लेंस से दूरी 90 – x = 90 – 60 = 30 cm होगी।
विशेष तथ्य –
1. अवतल लेंस के लिये चिन्ह परिपाटी
f(फोकस दूरी) = — (ऋणात्मक)
(वस्तु की दूरी) = – (ऋणात्मक) ।
(प्रतिबिम्ब की दूरी) = – (ऋणात्मक)
वस्तु का आकार (O) = + धनात्मक
प्रतिबिम्ब का आकर (h’) = धनात्मक (+ 1)
m (आवर्धन) = + धनात्मक
2. अज्ञात राशि का चिन्ह नहीं लेते, वह स्वयं प्रश्न को हल करते समय निकलकर आता है।

प्रश्न 19.
एक अवतल लेंस की फोकस दूरी 15 cm है। इस लेंस से 10 cm दूर रखी वस्तु के प्रतिबिम्ब की स्थिति तथा प्रकृति बताइए।
हल:
प्रश्नानुसार, अवतल लेंस की फोकस दूरी (f)= – 15 cm
वस्तु की अवतल लेंस से दूरी (u) = – 10 cm
लेंस से प्रतिबिम्ब की दूरी (v) = ?
लेंस के सूत्र

या v=-6 cm
ऋण चि से स्पष्ट है कि प्रतिबिम्ब वस्तु की ओर बनता है तथा लेंस से 6 cm दूर, आभासी, छोटा व सीधा बनता है।
प्रश्न 20.
कोई बिम्ब 30 सेमी फोकस दूरी के किसी अवतल लेंस से 60 सेमी दूरी पर स्थित है।
(i) लेंस सूत्र का उपयोग करके लेंस से प्रतिबिम्ब की दूरी ज्ञात कीजिए।
(ii) इस प्रकरण में बनने वाले प्रतिबिम्ब के चार अभिलक्षणों (प्रकृति, स्थिति, आकार, सीधा/उल्टा) की सूची बनाइए।
(iii) भाग (ii) में दिए गए अपने उत्तर की पुष्टि के लिए किरण आरेख खींचिए। (CBSE 2019)
हल:
(i) f=-30 सेमी, u =-60 सेमी लेंस सूत्र से,
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(-\frac{1}{30}=\frac{1}{v}-\frac{1}{(-60)}\)
\(\frac{1}{v}=\frac{1}{-30}-\frac{1}{60}\)
⇒ \(\frac{1}{v}=\frac{-2-1}{60}\)
v = \(-\frac{60}{3}\) = -20 सेमी
(ii) हम जानते हैं- m= \(\frac{h^{\prime}}{h}=\frac{v}{u}\)
m = \(\frac{-20}{-60}=\frac{1}{3}\)
इससे तात्पर्य है कि प्रतिबिम्ब आभासी, वस्तु की ओर प्रकाशीय केन्द्र व फोकस के मध्य, वस्तु के आकार का 1e3 बनेगा। प्रतिबिम्ब सीधा बनेगा।
(iii)
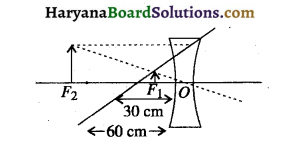
प्रश्न 21.
अनन्त से आने वाली किरणें जब अवतल लेंस पर पड़ती हैं तो लेंस से 30 सेमी. की दूरी पर प्रतिबिम्ब बनता हुआ प्रतीत होता है। जब इस लैंस के सामने 3 सेमी. ऊँचा बिम्ब, लेंस से 15 सेमी. की दूरी पर रखा जाता है तो बनने वाले प्रतिबिम्ब की स्थिति एवं आकार की गणना कीजिये।
हल:
सर्वप्रथम –
u= – ∞
v=- 30 सेमी
f=?
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{-30}+\frac{1}{\infty}\)
\(\frac{1}{f}=-\frac{1}{30}\)
f=-30 cm
अत: h = 3 सेमी., h’ = ?
u=- 15 सेमी.

अतः प्रतिबिम्ब लेंस से 10 सेमी. की दूरी पर उसी तरफ बनता है जिस तरफ बिम्ब रखा है। प्रतिबिम्ब का आकार 2 सेमी बनता हुआ प्रतीत होता है।
प्रश्न 22.
2.5 cm ऊँचाई का कोई बिम्ब 10 cm फोकस दूरी के किसी उत्तल लेंस के प्रकाशिक केन्द्र ‘0’ से 15 cm दूरी पर स्थित है। बनने वाले प्रतिबिम्ब की स्थिति और साइज़ ज्ञात करने के लिए किरण आरेख खींचिए। इस आरेख में प्रकाशिक केन्द्र ‘0’, मुख्य फोकस F तथा है. प्रतिबिम्ब की ऊँचाई अंकित कीजिए।
हल :
(i) h = 2.5 cm, u=-15 cm,
f= 10 cm, v=?, h = ?
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}, \frac{1}{v}=\frac{1}{f}+\frac{1}{u}\)
∴ \(\frac{1}{v}=\frac{1}{10}+\frac{1}{-15}\)
\(\frac{1}{v}=\frac{3-2}{30} \Rightarrow \quad \frac{1}{v}=\frac{1}{30}\)
∴ v=30 cm
प्रतिबिम्ब की स्थिति में, लेंस के दूसरी तरफ 30 cm दूरी पर।
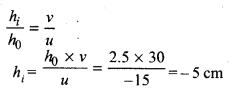
प्रतिबिम्ब का आकार = 5 cm (उल्टा बनेगा)
(ii)
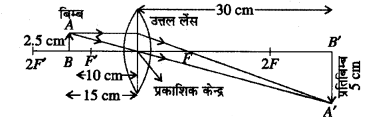
प्रश्न 23.
यदि किसी लेंस की फोकस दूरी 0.2 मीटर हो तो उसकी क्षमता चिह्न सहित ज्ञात कीजिए।
हल:
प्रश्नानुसार, लेंस की फोकस दूरी (f) = 0.2
मीटर लेंस की क्षमता (P) = ?
∴ लेंगी :. लेंस की क्षमता (P) = \(\frac{1}{f(\text { मी) में }}=\frac{1}{0.2} \)
अतः P=+5 डायोप्टर
प्रश्न 24.
25 cm फोकस दूरी के अवतल लेंस की क्षमता ज्ञात कीजिए।
हल:
अवतल लेंस की क्षमता (P) = \(\frac{100}{f(\mathrm{~cm} \text { में) }}=\frac{100}{-25} \)
P=-4D
प्रश्न 25.
एक अभिसारी लैंस जिसकी क्षमता +2.5D है, जिसे एक अपसारी लैंस जिसकी क्षमता – 3.0 D है के सम्पर्क में रखा जाता है। इस संयोजन से बने लैंस की क्षमता तथा फोकस दूरी की गणना कीजिए।
हल : अभिसारी लैंस की क्षमता (P1) = + 2.5 D
अपसारी लैंस की क्षमता (P2) = – 3.0 D
संयोजन की क्षमता (P) = P1 + P2
=+2.5-3.0
=-0.5D
संयोजन की फोकस दूरी (F) = \(\frac{100}{P}\) सेमी.
= \(\frac{100}{-0.5}\) =-200 सेमी.
बहुविकल्पीय प्रश्न (Objective Type Questions)
1. समतल दर्पण का आवर्धन होता है
(a) +1
(b)-1
(c) 0
(d).
उत्तर-
(a)
+1.
2. दूर स्थित किसी ऊँची इमारत के प्रतिबिम्ब को निश्चित रूप से किसके द्वारा देखा जा सकता है –
(a) अवतल दर्पण
(b) उत्तल दर्पण
(c) समतल दर्पण
(d) अवतल और समतल दर्पण।
उत्तर-
(b) उत्तल दर्पण।
3. टॉर्च, सर्चलाइट और वाहनों के अग्रदीपों में बल्ब लगाए जाते हैं –
(a) परावर्तक के ध्रुव एवं फोकस के बीच
(b) परावर्तक के फोकस के बहुत निकट
(c) परावर्तक के फोकस एवं वक्रता केन्द्र के बीच
(d) परावर्तक के वक्रता केन्द्र पर।
उत्तर-
(b) परावर्तक के फोकस के बहुत निकट।
4. अवतल दर्पण द्वारा किसी वस्तु का प्रतिबिम्ब आभासी सीधा तथा वस्तु से बड़ा बनता है तब वस्तु की स्थिति होगी –
(a) वक्रता केन्द्र पर
(b) वक्रता केन्द्र से परे
(c) फोकस तथा वक्रता के बीच में
(d) दर्पण के ध्रुव तथा फोकस के बीच में।
उत्तर-
(d) दर्पण के ध्रुव तथा फोकस के बीच में।

5. किसी वस्तु को अवतल दर्पण और फोकस के बीच रखा जाता है, प्रतिबिम्ब बनेगा –
(a) अनन्त पर
(b) दर्पण के पीछे
(c)F पर
(d) वक्रता केन्द्र पर ।
उत्तर-
(b) दर्पण के पीछे।
6. किसी गोलीय दर्पण द्वारा प्रतिबिम्ब हमेशा सीधा बनता है जबकि आप कितनी भी दूर खड़े हों, दर्पण-
(a) समतल
(b) समतल या उत्तल
(c) उत्तल
(d) अवतल।
उत्तर-
(c) उत्तल।
7. साधारण दर्पण से परावर्तित होकर कौन-सा प्रतिबिम्ब बनता है –
(a) वास्तविक
(b) आभासी
(c) वास्तविक एवं आभासी दोनों
(d) इनमें से कोई नहीं
उत्तर-
(c) वास्तविक एवं आभासी दोनों।
8. यदि काँच का अपवर्तनांक 1.5 हो तो काँच में प्रकाश का वेग होगा –
(a) 2 x 108 m/s
(b) 3 x 108 m/s
(c) \(\frac{2}{3}\) x 108 m/s
(d) \(\frac{3}{2}[/latex x 108 m/s .
उत्तर-
(a) 2 x 108 m/s
∴ v=[latex]\frac{c}{\mu}=\frac{3 \times 10^8}{1.5}= \) = 1.5
9. कोई किरण पृष्ठ पर लम्बवत् आपतित होती है तब अपवर्तन कोण का मान है –
(a) 90°
(b)0°
(c) 45°
(d)60°.
उत्तर-
(b) 0°
10. एक काँच के गुटके (स्लैब) की क्षमता होगी-
(a) शून्य
(b) अनन्त
(c) शून्य से कम
(d) शून्य से अधिक।
उत्तर-
(a) शून्य।
11. प्रकाश का वेग, न्यूनतम होता है-
(a) निर्वात में
(b) जल में
(c) वायु में
उत्तर-
(d) काँच में।

12. निर्वात में प्रकाश का वेग है
(a) 3 x 108 m/s
(b) 3 x 1010 m/s
(c) 3 x 1011 km/s
(d) 3 x 109 m/s
उत्तर-
(a) 3 x 108 m/s
13. किसी माध्यम में प्रकाश का वेग, वायु में प्रकाश के वेग से कम है तो इस माध्यम का अपवर्तनांक होगा –
(a) 1
(b) 1 से कम
(c) 1 से अधिक
(d) 1 से कम या अधिक कुछ भी हो सकता है।
उत्तर-
(c) 1 से अधिक।
14. \(\frac{\sin i}{\sin r}\) = n को किस नियम से जाना जाता है?
(a) जूल का नियम
(b) स्नैल का नियम
(c) न्यूटन
(d) इनमें से कोई नहीं।
उत्तर-
(b) स्नैल का नियम।
15. लेंस की क्षमता ज्ञात करने का सूत्र है –
(a) P=4f
(b) P = \(\frac{f}{2}\)
(c) P = \(\frac{1}{f}\)
(d) P= \(\frac{1}{2f}\)
उत्तर-
(c) P = \(\frac{1}{f}\)
16. किसी उत्तल लेंस की फोकस दूरी क्या होगी, जिसकी वक्रता त्रिज्या 40 cm है –
(a) 20 cm
(b) 10 cm
(c) 15 cm
(d) 3 cm.
उत्तर-
(c) 20 cm.
17. एक उत्तल लेंस की फोकस दूरी 20 cm है, उसकी क्षमता है –
(a) +20 D
(b)-20 D
(c) +5D
(d)-5 D.
उत्तर-
(c) +5 D.
18. उत्तल लेंस द्वारा सूर्य का प्रतिबिम्ब बनता है –
(a) F पर
(b) 2 F से दूर
(c) F व 2F के मध्य
(d) 2F पर।
उत्तर-
(a) F पर।

19. एक लेंस बीच में से मोटा तथा किनारों पर से पतला है तब यह लेंस कौन-सा होगा?
(a) अवतल
(b) साधारण दर्पण
(c) उत्तल
(d) प्रिज्म।
उत्तर-
(c) उत्तल।
20. एक उत्तल लेंस की क्षमता का चिह्न
(a) धनात्मक होता है
(b) शून्य होता है
(c) ऋणात्मक होता है
(d) इनमें से कोई भी नहीं।
उत्तर-
(a) धनात्मक होता है।
21. यदि उत्तल लेंस के सामने वस्तु अनन्त व 2F के बीच रखी हो तो उसका प्रतिबिम्ब बनेगा –
(a) वास्तविक, उल्टा और बिन्दु आकार का
(b) आभासी, सीधा और वस्तु के आकार का
(c) वास्तविक, उल्टा और वस्तु से छोटा
(d) वास्तविक, उल्टा और वस्तु से बड़ा।
उत्तर-
(c) वास्तविक, उल्टा और वस्तु से छोटा।
सुमेलन सम्बन्धी प्रश्न (Matrix Type Questions)
निम्नलिखित को समेलित कीजिए-
| कॉलम (X) |
कॉलम (Y) |
| (i) उत्तल लेंस |
(A) फोकस दूरी धनात्मक |
| (ii) अवतल लेंस |
(B) फोकस दूरी शृणात्मक |
| (iii) लेंस की शक्ति |
(C) \( \frac{1}{f}=\frac{1}{v}+\frac{1}{u} \) |
| (iv) दर्पण |
(D) डाइऑप्टर |
| (v) लेंस |
(E) \( \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \) |
उत्तर-
| कॉलम (X) |
कॉलम (Y) |
| (i) उत्तल लेंस |
(A) फोकस दूरी धनात्मक |
| (ii) अवतल लेंस |
(B) फोकस दूरी शृणात्मक |
| (iii) लेंस की शक्ति |
(D) डाइऑप्टर |
| (iv) दर्पण |
(C) \( \frac{1}{f}=\frac{1}{v}+\frac{1}{u} \) |
| (v) लेंस |
(E) \( \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \) |
रिक्त स्थानों की पूर्ति कीजिए (Fill In the blanks)
1. दर्पण सूत्र ………………………… होता है।
उत्तर-
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
2. निर्वात में प्रकाश की चाल ………………………… होती है।
उत्तर-
3 x 108 m/s,
3. लेंस की क्षमता का मात्रक ………………………… होता है।
उत्तर-
डाइऑप्टर (D)

4. गोलीय दर्पण के ध्रुव तथा मुख्य फोकस के बीच की दूरी को दर्पण की ………………………… कहते हैं।
उत्तर-
फोकस दूरी,
5. वाहनों के अग्रदीपों में प्रकाश का शक्तिशाली समान्तर किरण पुंज प्राप्त करने में ………………………… का प्रयोग किया जाता है।
उत्तर-
अवतल दर्पण।
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()