HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.5

Question 1.
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Solution:

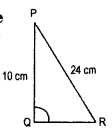
(PR)² = (PQ)² + (QR)²
⇒ (QR)² =(PR)² – (PQ)²
= (24)²-(10)²
= 576 – 100 = 476
∴ QR = \(\sqrt{476}\)
= \(\sqrt{2 \times 2 \times 7 \times 17}=\sqrt[2]{119}\)

Question 2.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.

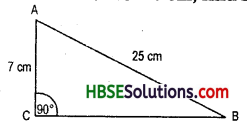
Solution:
(AB)² = (AC)² + (BC)²
(25)² = 7² + (BC)²
625-49 = (BC)²
576 = (BC)²
\(\sqrt{576}\) =, BC
24 = BC
∴  BC = 24 cm.

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance (Fig. 6.56). Find the distance of the foot of the ladder from the wall.
Solution:

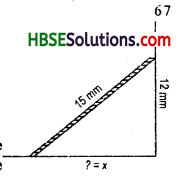
Let ? = x
(15)² = (12)² + x²
225 -144 = x²
81 = x²
\(\sqrt{81}\) = x
9 = x
∴  x = 9
The distance of the foot of the ladder from the wall = 9mm.

Question 4.
Which of the following can be the sides of a right triangle ?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right angled triangles, identify the right angles.
Solution:

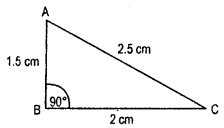
In a right triangle
h² = p² + b²
(iii) (1.5 cm, 2 cm, 2.5 cm) is the right angle
h² = p² + b²
(2.5)² = (1.5)² + (2)²
6.25 = 2.25 + 4
6.25 = 6.25
This is satisfied.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:

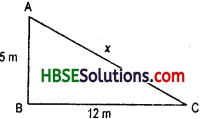
Let the original height of tree = x
∴  x² = (5)² + (12)²
= 25 + 144 = 169
∴  x = \(\sqrt{169}\)
∴ The original height of the tree = 13 m.

Question 6.
Angle Q and R of a APQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²

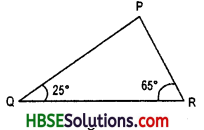
Solution:
∠QPR = 180° – (25° + 65°)
= 180°-90°
∴  ∠QPR = 90
By Pythagoras Property,
(QR)² = (PR)² + (PQ)²
i.e. h² = p² + b²
hence, QR² = (PQ)² + (RP)² i.e. (ii) is true.

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

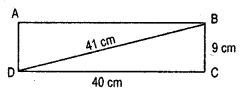
Solultion:
From Fig 6.88
(BC) = (BD) – (CD)
= (41) – (40)
= 1681 – 1600 = 81
∴  BC = \(\) = 9 cm.
Thus the perimeter of the rectangle
= 2 ( l x b) = 2(40 + 9)
= 2 x 49 = 98 cm.

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:

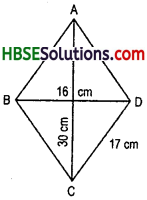
Area of Rhombus
= \(\frac{1}{2}\) x d₁ x d₂ Sq.units.

(where d₁ and d₂ are diagonals of rhombus) Side of Rhombus (a) = \(\frac{1}{2} \sqrt{\left(d_{1}\right)^{2}+\left(d_{2}\right)^{2}}\)
Perimeter of Rhombus = 4 x a
Here,
d₁ = 16 cm
d₂ = 30 cm
∴  Side of Rhombus (a)
= \(\frac{1}{2} \times \sqrt{(16)^{2}+(30)^{2}}=\frac{1}{2} \times \sqrt{256 \times 900}\)
= \(\frac{1}{2}\) x \(\sqrt{(16)^{2}+(30)^{2}}\) = \(\frac{1}{2}\) x 34 =17 cm z z
∴ Perimeter of Rhombuse
= 4 x a = 4 x 17= 68
∴ Perimeter of Rhombus = 68 cm.