Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.5 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.5
Question 1.
Use a suitable identity to get each of the following products :
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – \(\frac{1}{2}\))(3a – \(\frac{1}{2}\))
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a2 + b2) (-a2 + b2)
(vii) (6x- 7) (6x + 7)
(viii) (-a + c) (-a + c)
(ix) ![]()
(x) (7a – 9b) (7a – 9b).
Solution:
(i) ∵ (x + 9) (x + b)
= x2 + (a + b) x + ab
∴ (x + 3) (x + 3) = x2 + (3 + 3)x +3 × 3
= x2 + 6x + 9.
(ii) ∵ (a + b)2 = a2 + 2ab + b2
∴ (2y + 5) (2y + 5) = (2y + 5)2
= (2y)2 + 2 × 2y × 5 + (5)2
= 4y2 + 20y + 25.
(iii) (2a – 7) (2a – 7)
= (2a-7)2
[∵ (a – b)2 = a2 – 2ab + b2]
= (2a)2 – 2 × 2a × 7 + (7)2
= 4a2 – 28a+ 49.
(iv) (3a – \(\frac{1}{2}\))(3a – \(\frac{1}{2}\)) = (3a – \(\frac{1}{2}\))2
= (3a)2 – 2 × 3a × \(\frac{1}{2}\) + (\(\frac{1}{2}\))2
= 9a2 – 3a + \(\frac{1}{4}\)
(v) (1.1m -0.4) (1.1m + 0.4)
∵ (a + b) (a – b) = a2 – b2
∴ (1.1m + 0.4) (1.1m – 0.4)
= (1.1m)2 – (0.4)2
= 1.21m2 – 0.16.
![]()
(vi) (a2 + b2) (-a2 + b2) = (b2 + a2) (b2 – a2)
= (b2)2 – (a2)2 – b4 – a4.
(vii) (6x – 7) (6x + 7) = (6x)2 – (7)2
= 36x2 – 49.
(viii) (c -a) (c- a) = (c – a)2
= c2 – 2ca, + a2
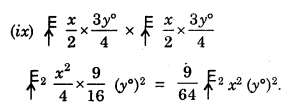
(x) (7a – 9b) (7a – 9b)
= (7a – 9b)2
= (7a)2 – 2 x 7a x 9b + (9b)2
= 49a2 – 126ab + 81b2.
![]()
Question 2.
Use the identity (x + a) (x + b) = x2 + (a + b) x + ab to find the following products :
(i) (x + 3) (x + 7)
(ii) (4x + 5) (4x + 1)
(iii) (4x – 5)(4x – 1)
(iv) (4x + 5)(4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a2 + 9) (2a2 + 5)
(vii) (xyz – 4) (xyz – 2).
Solution:
(i) (x + 3) (x + 7)
= x2 + (3 + 7)x + 3 × 7
= x2 + 10x + 21.
(iii) (4x + 5) (4x + 1)
= (4x)2 + (5 + 1)x + 5 × 1
= 16x2 + 6x + 5.
(iii) (4x – 5) (4x – 1)
= (4x)2 + [-5 + (-1)]x + (-5x – 1)
= 16x2 – 6x + 5.
(iv) (4x + 5) (4x – 1)
= (4x)2 + [5 + (-1)]x + [5 × (-1)]
= 16x2 + 4x – 5.
(v) (2x + 5y) (2x + 3y)
= (2x)2 + (5y + 3y)x + 5y × 3y
= 4x2 + 8xy + 15y2.
(vi) (2a2 + 9) (2a2 + 5)
= (2a2)2 + (9 + 5)2a2 + 9 × 5
= 4a4 + 28a2 + 45.
(vii) (xyz – 4) (xyz – 2)
= (xyz)2 + [(-4) + (-2)] xyz + (-4) x (-2)
= x2y2z2 – 6xyz + 8.
![]()
Question 3.
Find the following squares by using the identities :
(i) (b – 7)2
(ii) (xy + 3z)2
(iii) (6x2 – 5y)2
(iv) ![]()
(v) (0.4p – 0.5q)2
(vi) (2xy + 5y)2
Solution:
(i) b – 7)2 = b2 – 2 x b x 7 + 72
[∵ (a – b)2 = a2 – 2ab + b2]
= b2 – 14 b + 49.
(ii) (xy + 3z)2 = (xy)2 + 2 × xy × 3z + (3z)2
[∵ (a + b)2 = a2 + 2ab + b2]
= x2y2 + 6xyz2 + 9z2.
(iii) (6x2 – 5y)2 = (6x2)2 – 2 × 6x2 × 5y + (5y)2
= 36x4 – 60x2y + 25y2.
(iv) 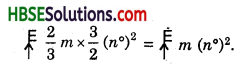
(v) (0.4p – 0.5q)2 = (0.4p)2 – 2 × 0.4p × 0.5q + (0.5q)2
= 0.16p2 – 0.40pq + 0.25q2.
(vi) (2xy + 5y)2 = (2xy)2 + 2 × 2xy × 5y + (5y)2
= 4x2y2 + 20xy2 + 25y2.
Question 4.
Simplify :
(i) (a2 – b2)2
(ii) (2x + 5)2 – (2x – 5)2
(iii) (7m – 8n)2 + (7m + 8n)2
(iv) (4m + 5n)2 + (5m + 4n)2
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
(vi) (ab + bc)2 – 2ab2c
(vii) (m2 – n2m)2 + 2m3n2.
Solution:
(i) (a2 – b2)2 = (a2)2 – 2 × a2 × b2 + (b2)2
= a4 – 2a2b2 + b4.
(ii) (2x + 5)2 – (2x – 5)2
= [(2x + 5) + (2x – 5)] [(2x + 5) – (2x – 5)]
= (2x + 5 + 2x – 5) (2x + 5 – 2x + 5)
= 4x × 10 = 40x.
(iii) (7m – 8n)2 + (7m + 8n)2
= (7m)2 – 2 × 7m × 8n + (8n)2 + (7m)2 + 2 × 7m × 8n + (8n)2
= 2 × (7m)2 + 2 × (8n)2.
= 2 × 49m2 + 2 × 64n2
= 98m2 + 128n2.
![]()
(iv) (4m + 5n)2 + (5m + 4n)2
= (4m)2 + 2 × 4m × 5n + (5n)2 + (5m)2 + 2 × 5m × 4n + (4n)2
= 16m2 + 40mn + 25n2 + 25m2 + 40mn + 16n2
= 41m2 + 41n2 + 80mn
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
= [(2.5p)2 – 2 × 2.5p × 1.5q + (1.5q)2] – [(1.5p)2 – 2 × 1.5p × 2.5q + (2.5q)2]
= 6.25p2 – 0.75pq + 2.25q2 – 2.25p2 + 0.75pq + 6.25q2
= 12.50p2.
(vi) (ab + bc)2 – 2ab2c
= (ab)2 + 2 × ab × bc + (bc)2 – 2ab2c
= a2b2 + 2ab2c + b2c2 – 2ab2c
= a2b2 + b2c2.
(vii) (m2 – n2m)2 + 2m3n2
= (m2)2 – 2 × m2 × n2m + (n2m)2 + 2m3n2
= m4 – 2m3n2 + n4m2 + 2m3n2 = m4 + n4m2.
![]()
Question 5.
Show that:
(i) (3x + 7)2 – 84x = (3x – 7)2
(ii) (9p – 5q)2 + 180pq = (9p + 5q)2
(iii) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
(iv) (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0.
Solution:
(i) (3x + 7)2 – 84= (3x – 7)2
L.H.S. = (32)2 + 2 × 3x × 7 + (7)2 – 84x
= 9x2 + 42x + 49 – 84x
= 9x2 – 42x + 49 = (3x – 7)2
= R.H.S. Hence proved.
(ii) (9p – 5q)2 + 180pg = (9q + 5q)2
L.H.S. = (9p)2 + 2 × 9p × 5q + (5q)2 + 180pg
= (9p)2 + 2 × 9pq × 5q + (5q)2
= (9p + 5q)2
= R.H.S. Hence proved.
(iii) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
L.H.S. = [(4pg + 3q) + (4pq – 3q)]
[(4pq + 3q) – (4pq – 3q)]
= (4pq + 3q + 4pq – 3g)
(4pq + 3q – 4pq + 3q)
= 8pq × 6q = 48pq2
= R.H.S. Hence proved.
(iv) (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
L.H.S. = a2 – b2 + b2 – c2 + c2 – a2 = 0
= R.H.S Hence proved.
![]()
Question 6.
Using identities, evaluate.
(i) (71)2
(ii) (99)2
(iii) (102)2
(iv) (998)2
(v) (5.2)2
(vi) 297 × 303
(vii) 78 × 82
(viii) (8.9)2
(ix) 10.5 × 9.5
Solution:
(i) (70 + 1)2 = (70)2 + 2 × 70 × 1 + (1)2
= 4900 + 140 + 1
= 5041.
(ii) (99)2 = (100 – 1)2
= (100)2 – 2 × 100 × 1 + (1)2
= 10000 – 200 + 1 = 9801
(iii) (102)2 = (100 + 2)2
= (100)2 + 2 × 100 × 2 + (2)2
= 10000 + 400 + 4 = 10402.
(iv) (998)2 = (1000 – 2)2
= (1000)2 – 2 × 1000 × 2 + (2)2
= 1000000 – 4000 + 4
= 996004.
(v) (5.2)2 = (5 + 0.2)2
= (5)2 + 2 × 5 × 0.2 + (0.2)2
= 25 + 2.0 + 0.04 = 27.04.
(vi) 297 × 303 = (300 – 3) (300 + 3)
= (300)2 – (3)2
= 90000 – 9
= 89991
(vii) 78 × 82 = (80 – 2) (80 + 2)
= (80)2 – (2)2
= 6400 – 4
= 6396.
(viii) (8.9)2 = (9 – 0.1)2
= (9)2 – 2 × 9 × 0.1 + (0.1)2
= 81 – 1.8 + 0.01
= 79.21.
(ix) (10.5) × (9.5) = (10 + 0.5) (10 – 0.5)
= (10)2 – (0.5)2
= 100 – 0.25
= 99.75.
![]()
Question 7.
Using a2 – b2 = (a + b) (a – b), find
(i) (51)2 – (49)2
(ii) (1.02)2 – (0.98)2
(iii) (153)2 – (147)2
(iv) (12.1)2 – (7.9)2
Solution:
(i) (51 + 49) (51 – 49) = 100 × 2 = 200.
(ii) (1.02)2 – (0.98)2
= (1.02 + 0.98) (1.02 – 0.98)
= 2.00 × 0.04 = 0.08.
(iii) (153)2 – (147)2
= (153 + 147) (153 – 147)
= 200 × 6 = 1200.
(iv) (12.1)2 – (7.9)2 = (12.1 + 7.9) (12.1 – 7.9)
= 20.0 × 4.2 = 84.0 = 84.
Question 8.
Using
(x + a) (x + b) = x2 + (a + b) x + ab, find
(i) 103 × 104
(ii) 5.1 × 5.2
(iii) 103 × 98
(iv) 9.7 × 9.8.
Solution:
(i) (100 + 3) (100 + 4)
= (100)2 + (3 + 4) × 100 + 3 × 4
= 10000 + 700 + 12 = 10712.
(ii) (5 + 0.1) (5 + 0.2)
= 52 + (0.1 + 0.2) × 5 + (0.1 × 0.2)
= 25 + 0.02 × 5 + 0.02
= 25 + 0.10 + 0.02
= 25.12.
![]()
(iii) (100 + 3) (100 – 2)
= (100)2 + [3 + (-2)] × 100 + 3 × (-2)
= 10000 + 100 – 6
= 10094.
(iv) 9.7 × 9.8 = (10 – 0.3) (10 – 0.2)
= (10)2 + (-0.3 + (-o.2)] × 10 + (-0.3) × (-0.2)
= 100 – 5 – 0.06
= 94.94.