HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.4

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.4

Question 1.
Multiply the binomials.
(i) (2x + 5) and (4x- 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l + 0.5 m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q²) and 3(pq – 2q²)
(vi)
Solution:
(i) (2x + 5) × (4x – 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15.

(ii) (y – 8) × (3y – 4) = 3y² – 4y – 24y + 32
= 3y² – 28y + 32.

(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= 6.25l² + 1.25lm – 1.25lm + 0.25m²
= 6.25l² + 0.25m².

(iv) (a + 3b) × (x,+ 5)
= ax + 5a + 3bx + 15b
= ax + 3bx + 5a + 15b.

(v) (2pq + 3q²) × (3pq – 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²a² + 5pq³ – 6q⁴.

(vi)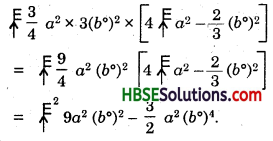

Question 2.
Find the product.
(i) (5 – 2x)(3 + x)
(ii) (x + 7y)(7x – y)
(iii) (a² + b) (a + b²)
(iv) (p² – q²) (2p + q).
Solution:
(i) (5 – 2x) × (3 + x)
= 15 + 5x – 6x – 2x²
= 15 – x – 2x².

(ii) (x + 7y) × (7x -y)
= 7x² – xy + 49xy – 7y²
= 7x² – 7y² + 48xy.

(iii) (a² + b) × (a + b²)
= a³ + a²b² + ab + b³
= a³ + b³ + a²b² + ab.

(iv) (p² – q²) × (2p + q)
= 2p³ + p²q – 2pq² – q³
= 2p³ – q³ + p²q – 2pq².

Question 3.
Simplify :
(i) (x² – 5) (x + 5) + 25
(ii) (a² + 5) (b³ + 3) + 5
(iii) (t + s²) (t² – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
(v) (x +y) (2x +y) + (x + 2y) (x – y)
(vi) (x + y) (x² – xy + y²)
(vii) (1.5x – 4y) (1.5x + 4y + 3)- 4.5x + 12y
(viii) (a + b + c) (a + b – c).
Solution:
(i) (x² – 5) × (x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x.

(ii) (a² + 5) × (b³ + 3) + 5
= a²b³ + 3a² + 5b² + 15 + 5
= a²b³ + 3a² + 5b³ + 20.

(iii) (t + s²) (t² – s)
= t³ – st + s²t² – s³
= t³ – s³ + s² + t² – st.

(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac +bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac.

(v) (x + y) × (2x + y) + (x + 2y) x (x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 3x² – y² + 4xy.

(vi) (x + y) × (x² – xy + y²)
= x³ – x²y + xy² + x²y – xy² + y³
= x³ + y³.

(vii) (1.5x – 4y) × (1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 60xy + 4.5x – 60xy – 16y² – 12y – 4.5x + 12y
= 2.25x².

(viii) (a + b + c) × (a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + b² – c² + 2ab.