HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities InText Questions

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities InText Questions

Try These (Page 138)

Question 1.
Give five examples of expressions containing one variable and five examples of expression containing two variables.
Solution:
One variable :
(i) x + 3,
(ii) x + 4,
(iii) y + 3,
(iv) 2 + 5,
(v) p + 2.

Two variables :
(i) 2xy + 3,
(ii) 3xy + 4,
(iii) 5xy + 3,
(iv) zx + 9,
(v) 2pq + 3.

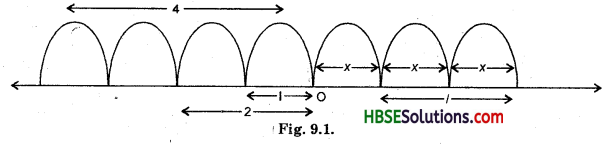
Question 2.
Show on the number line x, x – 4, 2x + 1, 3x – 2.
Solution:

Identify the coefficient of each term in the expression
x²y – 10x²y + 5xy – 20
Coefficient of x²y = 1
Coefficient of -10x²y = -10
Coefficient of 5xy = 5.

Question 3.
Classify the following polynomials as monomials, binomials, trinomials
-z + 5, x + y + z, y + z + 100, ab – ac, 17.
Solution:
Monomials : 17
Binomials : -z + 5, ab – ac
Trinomials : x + y + z, y + z + 100.

Question 4.
Construct:
(a) 3 binomials with only x as a variable;
(b) 3 binomials with x and y as variables;
(c) 3 monomials withx and y as variables;
(d) 2 polynomials with 4 or more terms.
Solution:
(a) x + 2, 2x + 5, 3x + 1
(b) 2xy + 3, 3xy + 7, 4xy + 2
(c) xy, x²y², 4x³y³ .
(d) a + b + c + d, 3x + 2y + z + 5

Try These (Page 139)

Question 1.
Write two terms which are like
(i) 7xy,
(ii) 4mn²,
(iii) 2l.
Solution:
(i) (7xy + 2); (14xy + 3)
(ii) (4mn² – 1); (6mn² + 2)
(iii) (2l + 5); (4l + 3).

Try These (Page 142)

Question 1.
Can you think of two more such situations, where we may need to multiply algebraic expressions ?
[Hint: (i) Think of Speed and Time, (ii) Think of interest to be paid, the principal and the rate of simple interest etc.]
Solution:
(i) Speed = \(\frac{Distance}{Time}\)
s = \(\frac{d}{t}\)
⇒ d = s × t

(ii) Simple Interest
= \(\frac{Principal × Rate × Time}{100}\)
⇒ S.I. = \(\frac{P × R × T}{100}\)
⇒ P × R × T = S.I. × 100

Try These (Page 143)

Question 1.
Find 4x × 5y × 7z.
First find 4x × 5y and multiply it by 7r; or first find 5y × 7z and multiply it by 4x.
Is the result the same ? What do you observe?
Does the order in which you carry out the multiplication matter ?
Solution:
4x × 5y × 7z = (4x + by) × 8z
= (20xy) × 7z
= 140 xyz.

Try These (Page 144)

Question 1.
Find the product:
(i) 2x(3x + 5xy)
(ii) a²(2ab – 5c).
Solution:
(i) 2x(3x + 5xy)
= (2 × 3)x² + (2 × 5)x²y
= 6x² + 10x²y.

(ii) a²(2ab – 5c) = 2a³b – 5a²c.

Try These (Page 145)

Question 1.
Find the product (4p² + 5p + 7) × 3p.
Solution:
(4p² + 5p + 7) × 3p
= 12p³ + 15p² + 21p.

Try These (i) (Page 149)

Question 1.
Put -6 in place of 6 in Identity (I). Do you get Identity (II) ?
Solution:
Identity I
⇒ (a + b)² = a² = a² + 2ab + b²
If b = -b.
⇒ [a + (-b)]² = a² + 2a(-b) + (-b)²
⇒ (a – b)² = a² – 2ab + b²
Hence Identity-II verified.

Try These (ii) (Page 149)

Question 1.
Verify identity (IV), for a = 2, b = 3, x = 5.
Solution:
∵ (x + a) (x + b) = x² + (a + b)x + ab
If, a = 2, b = 3, x = 5
Then (x + a) (x + b)
= (5)² + (2 + 3) × 5 + 2 × 3
= 25 + 25 + 6 = 56.

Question 2.
Consider, the special case of identity (IV) with a = b, what do you get ? Is it related to identity (I) ?
Solution:
If a = b,
Then, (x + a) (x + b) = x² + (b + b) x + b × b
= x² + 2bx + b².

Question 3.
Consider, the special case of identity (IV) with a = -c and b = -c. What do you get ? Is it related to identity (II) ?
Solution:
If a = -c and b = -c
Then, (x + a) (x + b)
= x² + [(-c) + (-c)] x + (-c × -c)
= x² – 2cx + c².

Question 4.
Consider the special case of identity (IV) with b = -a. What/ do you get ? Is it related to identity (III) ?
Solution:
If b = -a,
Then, (x + a) (x + b)
= x² + [a + (-a)]x + a × (-a)
= x² + (a – a) x – a²
= x² + 0 – a²
= x² – a²
= (x + a) (x – a).