Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.6 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise
14.6
Question 1.
Draw ∠POQ measures 75° and find its line of symmetry.
Solution:
steps of Construction :
(i) Construct ∠QOA = 90° and ∠QOB = 60° as shown above.
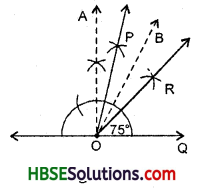
(ii) Draw \(\overrightarrow{\mathrm{OP}}\) as the bisector of ∠AOB.
(iii) Thus, ∠POQ is the required angle of measure 75°.
(iv) Draw \(\overrightarrow{\mathrm{OR}}\) as the bisector of ∠POQ which is the required line of symmetry.
![]()
Question 2.
Draw an angle of measure 147° and construct its bisector.
Solution:
Steps of Construction :
(i) Draw a ray \(\overrightarrow{\mathrm{OA}}\).
(ii) With the help of protector construct ∠AOB = 147°.
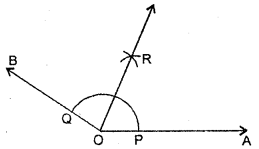
(iii) With centre ‘O’ and a convient radius, draw an arc which intersects
the arms \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\) at P and Q respectively.
(iv) With P as centre and radius more than half of PQ, draw an arc.
(v) With Q as centre and with the same radius, draw an other arc which intersects the previous arc at R.
(vi) Join OR and produce it. Thus, \(\overrightarrow{\mathrm{OR}}\) is the required bisector of ∠AOB.
Question 3.
Draw a right-angle and construct its bisector.
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘0’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at A and B.
which intersect each other at C.
(iv) Join OC. Thus, ∠COQ is the required right-angle.
(v) With B and E as centres and radius
more than half of BE, draw two arcs which intersect each other at the point D.
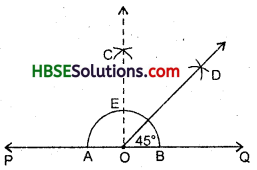
(vi) Join OD. Thus, \(\overrightarrow{\mathrm{OD}}\) is the required bisector of ∠COQ.
![]()
Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Solution:
Steps of Construction :
(i) Draw a ray \(\overrightarrow{\mathrm{OA}}\) .
(ii) At 0, with the help of a protector, construct ∠AOB = 153°.
(iii) Draw \(\overrightarrow{\mathrm{OC}}\) as the bisector of ∠AOB.
(iv) Again, draw \(\overrightarrow{\mathrm{OD}}\) as the bisector of ∠AOC.
(v) Again, draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠BOC.

Thus \(\overrightarrow{\mathrm{OD}}\), \(\overrightarrow{\mathrm{OC}}\) and \(\overrightarrow{\mathrm{OE}}\) divide ∠AOB into four equal parts.
Question 5.
Construct with ruler and compasses angles of following measures:
(a) 60°,
(b) 30°,
(c) 90°,
(d) 120°,
(e) 450,
(f) 135°.
Solution:
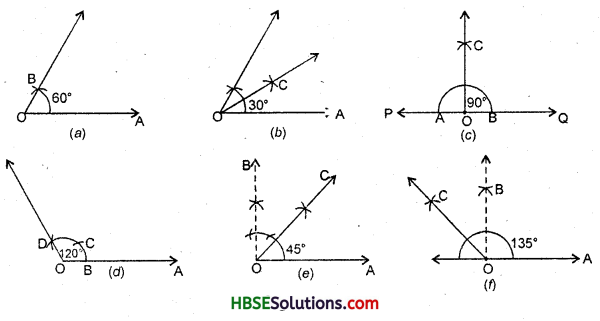
(a) ∠AOB = 60° (b) ∠AOC = 30°
(c) ∠QOC = 90° (d) ∠AOD = 120°
(e) ∠AOC = 45° (/) ∠AOC = 135°.
![]()
Question 6.
Draw an angle of measure 45° and bisect it. What is the measure of each angle you obtain ?
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘O’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at two points A and B.
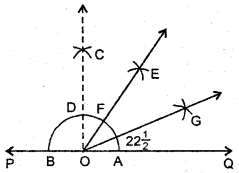
(iii) With A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(iv) Join OC. Then ∠COQ is an angle of 90°.
(v) Draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠COE. Thus, ∠QOE = 45°.
(vi) Now, draw OG as the bisector of ∠QOE. Thus, ∠QOG = ∠EOG = 22\(\frac{1}{2}\)°
Question 7.
Draw an angle of measure 135° and bisect it. What is the measure of each angle you obtain ?
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘O’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at A.and B.
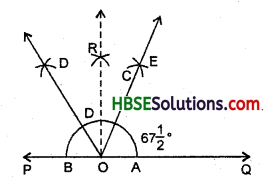
(iii) With A and B as centres and radius more than half of AB, draw two arcs which intersect each other at R.
(iv) Join OR. Then, ∠QOR = ∠POR = 90°.
(v) Draw \(\overrightarrow{\mathrm{OD}}\) as the bisector of ∠POR. Then, ∠QOD is the required angle of 135°.
(vi) Now, draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠QOD. Thus, ∠QOE = ∠DOE = 67\(\frac{1}{2}\)°