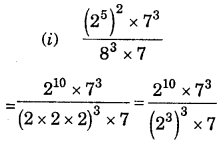HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers Ex 13.2

Haryana State Board HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers Ex 13.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 13 Exponents and Powers Exercise 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² x 3⁴ x 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ x a²
(iv) 7^x x 7²
(v) (5²)³ ÷ 5³
(vi) 2⁵ x 5⁵
(vii) a⁴ x b⁴
(viii) (3⁴)³
(ix) (2⁵⁰ ÷ 2¹⁵) x 2³
(x) 8^t ÷ 8²
Solution:
(i) 3² x 3⁴ x 3⁸ = 3^{2 + 4 + 8} = 3¹⁴
(ii) 6¹⁵ 6¹⁰ = \(\frac{6^{15}}{6^{10}}\) = 6^{15 – 10} = 6⁵
(iii) a³ x a² = a³⁺² = a⁵
(iv) 7^x x 7² = 7^x+2
(v) (5²)³ ÷ 5³ = \(\frac{5^{6}}{5^{3}}\) = 5^6-3 = 5³.
(vi) 2⁵ x 5⁶ = (2 x 5)⁵ = 10⁵.
(vii) a⁴ x b⁴ = (ab)⁴.
(viii) (3⁴)³ = 3^{4 x 3} = 3¹².

(ix) (2²⁰ ÷ 2¹⁵) x 2³ = \(\frac{2^{20}}{2^{15}}\) x 2³
=2^20-15 x 2³
= 2⁵ x 2³ = 2⁵⁺³ = 2⁸.

(x) 8^t ÷ 8² = \(\frac{8^{t}}{8^{2}}\) = 8^t-2.

Question 2.
Simplify and express each of the following in exponential form :

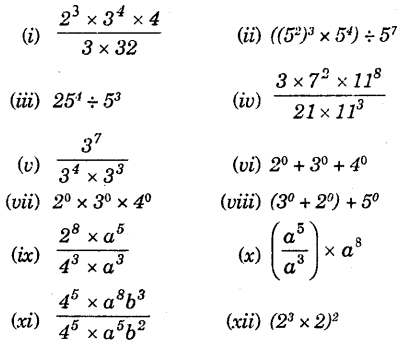
Solution:


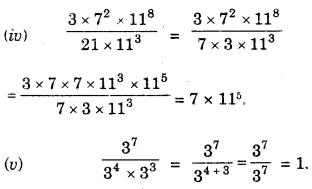
(vi) 2° + 3° + 4° = 2°(1 + 2°) + 3° .
(vii) 2° x 3° x 4° = (2 x 3 x 4)° = (24)°.
(viii) (3° + 2°) x 5° = (1 + 1) x 1
= 2 x 1 = 2¹.

(xii) (2³ x 2)² = 2^{3 x 2} x 2²
= 2⁶ x 2² = 2⁶⁺² = 2⁸

Question 3.
Say true or false and justify your answer:
(i) 10 x 10¹¹ = 100¹¹
(ii) 2³ x 5²
(iii) 2³ x 3² = 6⁵
(iv) 3⁰ = (1000)⁰
Solution:
10 x 10¹¹ = 100¹¹
= 10^{1 + 11} = 10¹²
= (10²)¹¹ = 10²²
L.H.S ≠ R.H.S
10 x 10¹¹ = 100¹¹ is false.

(ii) 2³ > 5²
L.H.S. 2³ = 8
R.H.S. 5² = 25
∴ 5² > 2³
2³ > 5² is false.

(iii) 2³ x 3² = 65
L.H.S. 2³ x 3²
R.H.S.
6⁵ = (2 x 3)⁵ = 2⁵ x 3⁵
∴ L.H.S. ≠ R.H.S.
∴ 2³ x 3² = 6⁵ is false.

(iv) 3⁰ = (1000)⁰
L.H.S.
3⁰
R.H.S.
1000⁰ = (10³)⁰
∴ L.H.S. ≠ R.H.S.
∴ 3⁰ = (1000)⁰ is false.

Question 4.
Express each of the following as a product of prime factor only in exponential form:
(i) 108 x 192
(ii) 270
(iii) 729 x 64
(iv) 768
Solution:
(i) 108 x 192
= 2 x 2 x 3 x 3 x 3 x 2 x 2 x 2 x 2 x 2 x 2 x 3
= 2⁸ x 3⁴.

(ii) 270
= 2 x 5 x 3 x 3 x 3
= 2 x 5 x 3³.

(iii) 729 x 64
= 3 x 3 x 3 x 3 x 3 x 3 x 2 x 2 x 2 x 2 x 2 x 2
= 3⁶ x 2⁶ = (3 x 2)⁶.

Question 5.
Simplify :
(i) \(\frac{\left(2^{5}\right)^{2} \times 7^{3}}{8^{3} \times 7}\)
(ii) \(\frac{25 \times 5^{2} \times t^{8}}{10^{3} \times t^{4}}\)
(iii) \(\frac{3^{5} \times 10^{5} \times 25}{5^{7} \times 6^{5}}\)
Solution: