Haryana State Board HBSE 9th Class Science Solutions Chapter 9 Force and Laws of Motion Textbook Exercise Questions and Answers.
Haryana Board 9th Class Science Solutions Chapter 9 Force and Laws of Motion
HBSE 9th Class Science Force and Laws of Motion Intext Questions and Answers
Questions from Sub-section 9.1, 9.2, 9.3
Question 1.
Which of the following has more inertia:
(a) a rubber ball and a stone of the same size?
(b) a bicycle and a train?
(c) a five-rupee coin and a one-rupee coin?
Answer:
(a) The inertia of stone will be more, in a rubber ball and a stone of the same size.
(b) In a bicycle and a train, the inertia of the train will be more.
(c) In a five-rupee coin and a one-rupee coin, the inertia of a five-rupee coin will be more.
Question 2.
In the following example, try to identify the number of times the velocity of the ball changes: “A football player kicks a football to another player of his team who kicks the football towards the goal. The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team.” Also identify the agent supplying the force in each case.
Answer:
The velocity of the ball changes four times as explained below:
(i) When the player kicks the ball.
(ii) When the second player kicks the ball towards the goal.
(iii) When the goalkeeper collects the ball.
(iv) When the goalkeeper kicks the ball towards the player of his own team.
The agent of force in each case is the muscular effort of the respective player.
Question 3.
Explain why some of the leaves may get detached from a tree if we vigorously shake its branch ?
Answer:
When branches of a tree are shaken vigorously, the leaves get detached from the tree. This is because the branches of the tree come into motion whereas the leaves tends to remain at rest due to inertia of rest. Thus, the leaves get detached from the branches and fall down under the action of gravity.
![]()
Question 4.
Why do you fall in the forward direction when a moving bus brakes to a stop and fall backwards when it accelerates from rest ?
Answer:
When a moving bus stops suddenly, the lower part of our body in contact with the bus comes to rest immediately, whereas the upper part of the body tends to move in forward direction due to inertia of motion and we fall in the forward direction.
But, when the bus accelerates from rest, the lower part of our body comes into motion alongwith the bus but the upper part of the body has tendency to remain in the state of rest due to inertia of rest and we fall in backward direction.
Questions from Sub-section 9.4, 9.5, 9.6
Question 1.
If action is always equal to the reaction, explain how a horse can pull a cart ?
Answer:
According to third law of motion, the action is always equal to reaction. When the horse pulls the cart, it acts on earth by a force F, the earth offers it reaction R, which has two components R cos A and R sin A. The horizontal part R cos A pulls the cart in forward direction, whereas the vertical part R sin A reduces the frictional force between the road and cart. In this way, the horse can pull the cart.
Question 2.
Explain, why it is difficult for a Fireman to hold a hose, which ejects large amounts of water at a high velocity ?
Answer:
According to third law of motion, the action is always equal to reaction. When the excess water comes out of the hose with high velocity, then it recoils the hose with same amount of velocity in backward direction. Therefore, it becomes difficult for a fireman to hold a hose.
![]()
Question 3.
From a rifle of mass 4 kg, a bullet of mass 50 g is fired with an initial velocity of 35 ms-1. Calculate the initial recoil velocity of the rifle.
Solution:
Here,
Mass of the bullet (m1) = 50g = 0.05 kg
Mass of the rifle (m2) = 4 kg
The initial velocity of bullet (u1) and the initial velocity of the rifle (u2) is zero.
or u1 = u2 = 0
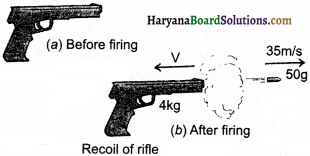
Velocity of bullet (v,) = + 35 ms-1
The direction of bullet, from left to right is taken + ve according to figure.
Let the recoil velocity of rifle = v ms-1
The total momentum of bullet and rifle before firing = (4 + 0.05) kg x 0 ms-1 = 0
Total momentum of bullet and rifle after firing = 0.05 kg × 35 ms-1 + 4 kg x v ms-1 = (1.75 + 4 v) kg ms-1
According to the law of conservation of momentum,
Total momentum after firing = Total momentum before firing
1.75 + 4 v = 0
v = –\(\frac{-1.75}{4}\) = -0.4375 = -0.44 ms-1
Negative sign shows that rifle will recoil in the opposite direction or right to left.
Question 4.
Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 ms-1 and 1 ms”1, respectively. They collide and after collision, the first object moves at a velocity of 1.67 ms”1. Determine the velocity of the second object.
Solution:
Here,
Mass of the first object (m1) = 100g = 0.1 kg
Mass of second object (m2) = 200 g = 0.2 kg
Initial velocity of first object (u1) = 2 ms-1
Initial velocity of second object (u2) = 1 ms-1
Total momentum of two objects before collision = m1u1 + m2u2
= (0.1 x 2 + 0.2 x 1) kg ms-1 = 0.4 kg ms-1
The velocity of first object after collision (v1) = 1.67 ms-1
Let, the velocity of second object after collision (v2) = v ms-1
Total momentum of two objects after collision = m1v1 + m2v2
= [0.1 x 1.67 + 0.2 x v2] kg ms-1
= [0.167 + 0.2 v2] kg ms-1
According to the law of conservation of momentum
Total momentum after collision = Total momentum before collision
0.167 + 0.2 v2 = 0.4
or 0.2v2 = 0.4 – 0.167
0.2v2 = 0.233
or v2 = \(\frac {0.233}{0.2}\) = 1.165 ms-1
The velocity of second object after collision = 1.165 ms-1
![]()
HBSE 9th Class Science Force and Laws of Motion Textbook Questions and Answers
Question 1.
An object experiences a net zero external unbalanced force. Is it possible for the object to be traveling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Answer:
Here, the external unbalanced force on an object is zero. It means,
F = 0
⇒ m a = 0
But, m ≠ 0 ∴ a = 0
It is possible to move in this state, but the motion will be in the same magnitude and in one direction or straight path.
Question 2.
When a carpet is beaten with a stick, dust comes out of it. Explain.
Answer:
When a carpet is beaten with a stick, it moves forward, whereas dust particles have a tendency to remain at rest due to the inertia of rest. Thus, dust particles come out and the carpet gets clean.
Question 3.
Why is it advised to tie any luggage kept on the roof of a bus with a rope?
Answer:
It is advised to tie any luggage kept on the roof of a bus with a rope because when the moving buses or cars suddenly stop or change direction, the luggage becomes safe from falling due to inertia of motion.
Question 4.
A batsman hits a cricket ball which then rolls on level ground. After covering a short distance, the ball comes to rest The ball slows to stop because:
(а) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest
(Choose the correct option)
Answer:
(c) There is a force on the ball opposing the motion.
![]()
Question 5.
A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 tonnes. [Hint: 1 tonne = 1000 kg]
Solution:
Here, Initial velocity in first stage (u) = 0
Distance covered (s) = 400 m
Acceleration (a) = ?
Time (t) = 20s
According to formula, s = ut + \(\frac {1}{2}\) at2
ut + \(\frac {1}{2}\) at2 = s
0 x (20) + \(\frac {1}{2}\) a x (20)2 = 400
200 a = 400
a = \(\frac {400}{200}\) = 2 ms-2
Mass in second stage (m) = 7 tones = 7 x 1000 = 7000kg
force (F) = m x a = 7000 kg x 2 ms-2 = 14000 N
Question 6.
A stone of 1 kg is thrown with a velocity of 20 ms-1 across the frozen surface of a lake and it comes to rest after traveling a distance of 50 ni. What i the force of friction between the stone and the ice?
Solution:
Here,
Mass of stone (m) = 1 kg
Initial velocity of stone (u) = 20 ms-1
Final velocity of stone (v) = 0
Distance covered by stone (s) = 50 m
Acceleration (a) = ?
We know that,
v2 – u2 = 2as .
a = \(\frac{v^2-u^2}{2 s}=\frac{(0)^2-(20)^2}{2(50)}\)
= \(\frac{-400}{100}\) = -4 ms-1
A negative (-ve) sign shows that acceleration is working against the motion.
The frictional force between the stone and the ice I (-4) = – 4N
Question 7.
An 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40000 N and (be track offers a friction force of 5000 N, then calculate:
(a) the net accelerating force,
(b) the acceleration of the train; and
(c) the force of wagon I on wagon 2.
Solution:
Here,
The mass of train engine (m1) = 8000 kg
Mass of 5 wagons(m2) 2000kg x 5 = 10000 kg
Mass of train engine with wagons (m) = m1 + m2 = (8000 + 10000)kg = 18000 kg
The force applied by the engine on wagons (F1) = 40000 N
The friction force applied by track on wagons (F2) = 5000 N
(a) The net acceleration force (F) = F1 – F2
40000N – 5000N = 35000N
![]()
(b) The acceleration of the train (a) = \(\frac{F}{m_2}=\frac{35000}{10000}\) ms-2 = 3.5 ms-2
(c) The force of wagon I ou wagon 2 35000 N – \(\frac{35000}{5}\) = (35000 – 7000) N = 28000N Ans
Question 8.
An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is tobe stopped with a negative acceleration of 1.7 ms-2?
Solution:
Here,
Mass of automobile vehicle (m) = 1500 kg
The acceleration on vehicle (a) = 17 ms-2
Final velocity (v) = 0
The force between the vehicle and road (F) = m x a = 1500 × (-1.7) N = -2550 N
Negative (-ve) sign shows that the force is working against the motion of vehicle.
Question 9.
What is the momentum of an object of mass m, moving with a velocity v ?
(a) (mv)2
(b) mv2
(c) \(\frac {1}{2}\) mv2
(d) mv (choose correct option from above)
Answer:
(d) mv.
Question 10.
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet?
Answer:
If we push the wooden cabinet with constant velocity on the floor by applying a force of 200 N, then the frictional force of the wooden cabinet will also be 200 N.
Question 11.
Two objects, each of mass 1.5 kg, are moving in the same straight line but in opposite directions. The velocity of each object is 2.5 ms-1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
Answer:
Here, the mass and velocity of both objects are the same, but both are moving in opposite directions, so they bend after the collision. Therefore, their combined velocity will be zero.
![]()
Question 12.
According to the third law of motion, when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the roadside, it will probably not move. A student justifies this by answering that the two opposite and equal forces cancel each other. Comment on this logic and explain why the truck does not move.
Answer:
The truck parked along the roadside will not move on applying force by us because the force applied by us is much less than the frictional force applied by the truck between the truck and the road. If our force increases to frictional force, the truck will move.
Question 13.
A hockey ball of mass 200 g traveling at 10 ms-1 is struck by a hockey stick so as to return it along its original path with a velocity at 5 ms-1. Calculate the change of momentum that occurred in the motion of the hockey ball by the force applied by the hockey stick.
Solution:
Here,
Mass of hockey ball (m) = 200 g = 0.2 kg
Initial velocity of hockey ball (v1) = 10 ms
The initial momentum of hockey ball travels in the opposite direction with velocity (v2) = 5 ms-1
Final Movemntum Of Hockey Boll = mv2
Change in momentum = mv1 – mv2 = 0.2 [10 – (-5)] = 0.2(15) = 3 kg ms-1
Thus, the change in momentum of the hockey ball is 3 kg ms-1
Question 14.
A bullet mass Logis traveling horizontally with a velocity of 150 m1 strikes a stationary wooden block and comes to at rest in 0.03 s. Calculate the distance of penetration of the bullet into the Mock. Also calculate the magnitude of the force exerted by the wooden block on the bullet.
Solution:
Here,
Mass of bullet (m) = 10g
= \(\frac {10}{1000}\) = 0.01kg
Initial velocity of bullet (u) = 150 ms-1
Final velocity of bullet (v) = 0 ms-1
Time (t) = 0.03 s
Acceleration (a) = ?
Distance (s) = ?
We know that,
a = \(\frac{v-u}{t}=\frac{0-150}{0.03}\) ms-2 = -5000 ms-2
and s = ut + at2
= (150)(0.03) + \(\frac {π}{2}\) × (-5000) x (0.03)2
= 4,5 – 2.25 = 2.25m
Force(F) = ma
= 0.01 x (-5000)N = -50 N
The negative (-ve) sign shows that force is working in the opposite direction of motion.
![]()
Question 15.
An object mass 1 kg traveling In a straight line with a velocity of 10 ms collides with and sticks to, a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the Impact. Also, calculate the velocity of the combined object.
Solution:
Here,
Mass of object (m) = 1 kg
Velocity of object (v1) = 10 ms-1
∴Momentum before collision = m x v1
= 1 x 1o kg ms-1 = 1o kg ms-1
The momentum after collision = 10 kg ms-1
Combined mass of wooden block and object (m1) = 5 + 1 = 6kg
Suppose. the final velocity of object and wooden block = v2 ms-1
According to the law of conservation of momentum,
m1 v2 = 10
or 6 x v2 = 10
0r v2 = \(\frac{10}{6}\) ms-1 = \(\frac{10}{6}\) ms-1
Question 16.
An object of mass loo kg Is accelerated uniformly from a velocity of S mr1 to 8 mr’ in 6s. object. Also, find the magnitude of the force exerted on the object
Solution:
Here.
Mass of object (m) = 100 kg
Initial velocity (u) = 5 ms-1
Final velocity (y) = 8 ms-1
Time(t) = 6s
Initial momentum = mu = 100 x 5 = 500 kg ms-1
Final momentum = mv = 100 x 8 = 800 kg ms-1
We know that,
a = \(\frac{v-u}{t}=\frac{8-5}{6}=\frac{3}{6}\) = 0.5 ms-2
The magnitude of the force (F) = m x a
= l00 x 0.5N = 1.50 N
![]()
Question 17.
Akhtar, ((Iran and Rbul were riding in a motorcar that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of the motorca (because the change in the velocity of the Insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul while putting an entirely new explanation said that both the motorcar and the insect experienced the same force and a change In their momentum. Comment on these suggestions.
Answer:
Akhtar was right because both the velocity and mass of the motorcar were moveso the momentum of the motorcar was more than that of flying insect. Therefore, the motorcar imposed much force on flying insect due to the insect died.
Question 18.
How much momentum will a dumbbell of mass 10 kg transfer to the floor if It falls from a height of 80cm? Take its downward acceleration to be 10 ms2 ?
Solution:
Here,
Mass of dumb-bell (m) = 10 kg
Initial velocity of dumb-bell (u) = 0 ms-1
Final velocity of dumbbell (v) = ?
Height of dumb-bell (s) = 80 cm = 0.8 m
Acceleration (a) = 10-2
We know that.
v2 – u2 = 2as
v2 – (0)2 = 2(10) (0.8)
v2 = 16
v = \(\sqrt{16}\) = 4 ms
Momentum transferred to the floor by dumb-bell (p) = mv = 10 x 4 = 40 kg ms
Additional Exercise Questions
Question 1.
The following is the distance-time table of an object in motion:
| Time (in seconds) | Distance (in metres) |
| o | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
| 6 | 216 |
| 7 | 343 |
(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing, orzero?
(b) What do you infer about the force acting on the object 1
Answer:
(a) It is clear from the distance-time table that acceleration is continuously increasing.
(b) The force is also increasing due to the increase in acceleration on body.
| Time (t) | Distance (s) | Velocity (v) = \(\frac {s}{t}\) | Acceleration (a) = \(\frac {v – u}{t}\) |
| t1 = 0s | s1 = 0 m | v<1 = 0 ms-1 | a1 = 0 ms-2 |
| t2 = 1 s | s2 = 1 m | v2 = 1 ms-1 | a2 = 1 ms-2 |
| t3 = 2 s | s3 = 8 m | v3 = 4 ms-1 | a3 = 3 ms-2 |
| t4 = 3 s | s4 = 27 m | v4 = 9 ms-1 | a4 = 5 ms-2 |
| t5 = 4S | s5 = 64 m | v5 = 16 ms-1 | a5 = 7 ms-2 |
| t6 = 5 s | s6 = 125 m | v6 = 25 ms-1 | a6 = 9 ms-2 |
| t7 = 6 S | s7 = 216 m | v7 = 36 ms-1 | a7 = 11 ms-2 |
| t8 = 7 s | s8 = 343 m | v8 = 49 ms-1 | a8 = 13 ms-2 |
Question 2.
Two persons manage to push a motorcar of mass 1200 kg at a uniform velocity along a level road. The same motorcar can be pushed by three persons to produce an acceleration of 0.2 ms-2.With what force does each person push the motorcar? (Assume that all persons push the motorcar with the same muscular effort.)
Solution:
Here,
Mass of motorcar (m) = 1200 kg
The acceleration produced on pushing by three persons
(a) = 0.2 ms-2
∴ The force imposed on car by each person (F) = m a = 1200 x 0.2N. = 240N Ans
Question 3.
A hammer of mass 500 g, moving at 50 m1, to strike a nail. The nail stops the hammer In a very short time of 0.01s. What Is the force of the nail on the hammer?
Solution:
Here,
Mass of hammer (m) = 500 g = \(\frac {500}{1000}\) kg = 0.5kg
Initial velocity of hammer (u) = 50 ms-1
Time (t) = 0.01 s
Final velocity of hammer (v) = 0
We know that,
Acceleration (a) = \(\frac{v-u}{t}=\frac{0-50}{0.01}\) = 0.01 ms-2
= -5000 ms-2
(-ve sign shows that acceleration is decreasing, i.e., retarded)
The force of the nail on the hammer (F) = m x a
= O.5 x (5000)N
= 2500N
![]()
Question 4.
A motorcar of mass 1200 kg Is moving along a straight line with a uniform velocity of 90 km/h. Its velocity Is slowed down to 18 km/h In 4 s by an unbalanced external force. Calculate the acceleration and change ¡n momentum. Also, calculate the magnitude of the force required.
Solution:
Here,
The mass of a motorcar (m) is 1200 kg
Initial velocity (u) = 90 km h-1= \(\frac{90 \times 1000}{3600}\) = 25 ms-1
Final velocity (v) = 18 km/h = \(\frac{18 \times 1000}{3600}\) = 5 ms-1
Tíme(t) = 4s
Acceleration (a) = \(\frac{v-u}{t}=\frac{5-25}{4}=\frac{-20}{4}\)
= -5 ms-2
Change ¡n momentum mv – mu
= m(v – u) = 1200(5 – 25) = 1200 x (-20) = -24000 kg ms-1
The magnitude of the force required (F) = m a
1200 x – 5 = – 6000N
Question 5.
A large truck and a car, both moving with a velocity of magnitude w, have a head-on collision and both of them come to a halt after that. If the collision for is:
(a) Which vehicle experiences the greater force of impact?
(b) Which vehicle experiences the greater change ¡n momentum?
(C) Which vehicle experiences the greater acceleration?
(d) Why is the car likely to suffer more damage than the truck?
Answer:
(a) Here, the mass of the truck is more than that of car, and the force of the truck will be more which affects the car more.
(b) Truck will experience a greater change in momentum.
(c) The acceleration of the car will be greater.
(d) Car will suffer from more damage because the mass of truck is more.