Haryana State Board HBSE 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.2 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals Exercise 3.2
Question 1.
Find x in the following figures :
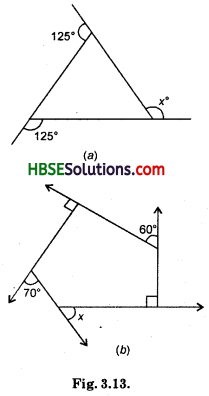
Solution:
(a)
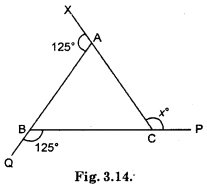
∠XAB + ∠BAC = 180°
or 125° + ∠BAC = 180°
∠BAC = 180° – 125° = 55
∴ ∠BAC = 55°
∠ABC + ∠QBC = 180°
∠ABC + 125° = 180°
∴ ∠ABC = 180° – 125° = 55°
In △ABC.∠A + ∠B + ∠C = 180°
55° + 55° + ∠C = 180°
110°+ ∠C = 180°
∴ ∠C = 180°-110° = 70°
∠ACB + ∠x = 180° [Linear pair]
70° + ∠x = 180°
∴ ∠x = 180°-70° = 110°
2nd Method : Sum of the measures of the external angles of any polygon is 360°.
∴ 125° + 125° + x = 360°
or 250° + x = 360°
∴ x = 360° – 250° = 110°
(b) ∠DCQ + ∠DCB = 180°
or 60° + ∠DCB = 180°
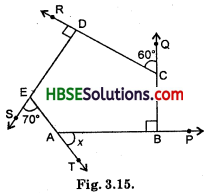
∴ ∠DCB = 180° – 60° = 120°
∠AES + ∠AED = 180°
70° + ∠AED = 180°
∠AED = 180° – 70° = 110°
∠RDE + ∠EDC = 180°
90° + ∠EDC = 180°
∴ ∠EDC = 90°
∠ABC + ∠CBP = 180°
90° + ∠CBP = 180°
∴ ∠CBP = 90°
∠SEA + ∠TAB + ∠CBP + ∠DCQ + ∠RDE = 360°
70° + x + 90° + 60° + 90° = 360°
or x + 310° = 360°
∴ ∠x = 360°-310°
∴ ∠x = 50°.
![]()
Question 2.
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides.
Solution:
(i)Total measure of all exterior angles = 360°
Total number of sides = 9
Therefore, the measure of each exterior angle = \(\frac{360}{9}\) = 40°
(ii) Total measure of all exterior angle = 360°
Total number of sides = 15
Therefore, the measure of each exterior angle = \(\frac{360}{15}\) = 24°
Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24° ?
Solution:
Total measure of all exterior angle = 360°.
The measure of an exterior angle is 24.
Therefore, the number of sides = \(\frac{360}{24}\) = 15.
∴ The number of sides = 15.
![]()
Question 4.
How many sides does a regular polygon have if each of its interior angles is 165°?
Solution:
Each interior angle of a polygon = 165°
∴ Each exterior angle = 180° – 165° = 15°
Sum of exterior angles = 360°
∴ Number of sides = \(\frac{360}{15}\) = 24
∴ Polygon has 24 sides.
Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22° ?
(b) Can it be an interior angle of a regular polygon ? Why ?
Solution:
(a) No; (since 22 is not a divisor of 360).
(b) No; because each exterior angle is 180° – 22° = 158°, which is not a divisor of 360°.
![]()
Question 6.
(a) What is the minimum interior angle possible for a regular polygon ? Why?
(6) What is the maximum exterior angle possible for a regular polygon?
Solution:
(a) The equilateral triangle being a regular polygon of 3 sides has the least measure of an interior angle = 60°.
(b) By (a), we can see that the greatest exterior angle = (180° – 60°) = 120°.