Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.2 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.2
Question 1.
If you subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), you get \(\frac{1}{8}\). What is the number ?
Solution:
Let, the number be x.
Subtract \(\frac{1}{2}\) from x and multiply the,result by \(\frac{1}{2}\).
∴ (x – \(\frac{1}{2}\)) × \(\frac{1}{2}\) = \(\frac{1}{8}\)

Question 2.
The perimeter of a rectangular swimming pool is 154 m. Its length is 2m more than twice its breadth. What are the length and the breadth of the pool ?
Solution:
Let the breadth of swimming pool be x
∴ Length = 2x + 2
The perimeter of swimming pool = 154 m.
or, 2(l + b) = 154
or, 2 (2x + 2 + x) = 154
or, 2 (3x + 2) = 154
or, 6x + 4 = 154
or, 6x = 154 – 4
or, 6x = 150
x = \(\frac{150}{6}\) = 25
∴ Breadth = 25 m.
Length = 2 × 25 + 2 = 52 m.
![]()
Question 3.
The base of an isosceles triangle is \(\frac{4}{3}\) cm. The perimeter of the triangle is 4\(\frac{2}{15}\) cm. What is the length of either of the remaining equal sides?
Solution:
Let the length of one equal side be x.
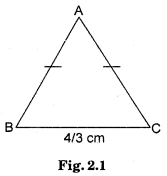
According to the question
AB + BC + AC = 4\(\frac{2}{15}\) cm
x + \(\frac{4}{3}\) + x = \(\frac{62}{15}\)
⇒ 2x = \(\frac{62}{15}\) – \(\frac{4}{3}\) = \(\frac{42}{15}\)
∴ x = \(\frac{4}{3}\) = \(\frac{21}{15}\)
= \(\frac{7}{5}\) = 1\(\frac{2}{5}\) cm
Question 4.
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:
Let other number be x.
First number will be x + 15
Sum of two numbers is 95
or, x + x + 15 = 95
or, 2x + 15 = 95
or, 2x = 95 – 15 = 80
x = \(\frac{80}{2}\) = 40
∴ Other number = 40
One number = 40 + 15 = 55
![]()
Question 5.
Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers ?
Solution:
Let the ratio be x. The numbers will be 5x and 3x
According to the question
5x – 3x = 18
⇒ 2x = 18
x = 9
∴ 5x = 5 × 9 = 45
3x = 3 × 9 = 27
The numbers are 45, 27
2nd Method
Let the numbers are x and y
∴ \(\frac{x}{y}\) = \(\frac{5}{3}\)
3x = 5y ⇒ x = \(\frac{5y}{3}\) ………(i)
2nd part of the question
x – y = 18
From (i)
\(\frac{5y}{3}\) – y = 18
\(\frac{5y-3y}{3}\) = 18
\(\frac{2y}{3}\) = 18
2y = 18 × 3 = 54
y = 27
From (i) x = \(\frac{5×27}{3}\) = 45
∴ Numbers are 45, 27
Question 6.
Three consecutive integers add up to 51. What are these integers ?
Solution:
Let first integer be x
Second integer be x + 1
Third integer be x + 1 + 1 = x + 2 (The differ from two consecutive integers is 1.)
According to the question
x + x + 1 + x + 2 = 51
⇒ 3x + 3 = 51
⇒ 3x = 51 – 3 = 48
x = 16
∴ First integer = 16
Second integer = 17
Third integer = 18
![]()
Question 7.
The sum of three consecutive multiples of 8 is 888. Find the multiples.
Solution:
Let the first multiple of 8 be 8x:
Second multiple be 8x + 8
Third multiple be 8x + 8 + 8 = 8x + 16
According to the question
8x + 8x + 8 + 8x + 16= 888
or, 24x + 24 = 888
or, 24x = 888 – 24
or, 24x = 864
x = \(\frac{864}{24}\) = 36
∴ 8x = 8 × 36 = 288
8x + 8 = 288 + 8 = 296
8x + 16 = 288 + 16 = 304
∴ The numbes will be 288, 296 and 304.
Question 8.
Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74. Find these numbers.
Solution:
Let the first number be x
The second number = x + 1
The third number = x + 1 + 1 = x + 2
According to the question
2x + 3 (x + 1) + 4 (x + 2) – 74
or, 2x + 3x + 3 + 4x + 8 = 74
or, 9x + 11 = 74
or, 9x = 74 – 11 = 63
∴ x = \(\frac{36}{9}\) = 7
∴ The first number = 7
Second number = 7 + 1 = 8
Third number = 7 + 2 = 9
![]()
Question 9.
The ages of Rahul and Ilaroon are in the ratio 5 : 7. Four years later the sum of their ages will be 56 years. What are their present ages?
Solution:
Let the ratio be x
Rahul’s present age = 5x years
Haroon’s present age = 7x years
Four years later Rahul’s age will be 5x + 4 years
Four years later Haroon’s age will be 7x + 4 years
According to the question
5x + 4 + 7x + 4 = 56
12x + 8 = 56
or, 12x = 56 – 8 = 48
x = \(\frac{48}{12}\) = 4
∴ Rahul’s present age = 5 × 4 = 20 years
Haroon’s present age = 7 × 4 = 28 years
Question 10.
The number of boys and girls in a class are in the ratio 7 : 5. The number of boys is 8 more than the number of girls. What is the total class strength ?
Solution:
Let the ratio be x.
The number of boys = 7x
The number of girls = 5x
According to the question
7x – 5x = 8
or, 2x = 8
∴ x = 4
Therefore number of boys = 7 × 4 = 28
The number of girls = 5 × 4 = 20
The total class strength = 28 + 20 = 48.
![]()
Question 11.
Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than Baichung’s. The sum of the ages of all the three is 135 years. What is the age of each one of them?
Solution:
Let Baichung’s age be x years.
Baichung’s Father age
= x + 29 years
Baichung’s Grand father age
= x + 29 + 26
= x + 55 years.
The sum of the ages of all the three is 135 years
∴ x + x + 29 + x + 55 = 135
or, 3x + 84 = 135
or, 3x = 135 – 84 = 51
x = \(\frac{51}{3}\) = 17
Baichung’s age = 17 years
Baichung’s father age
= 17 + 29 = 46 years
Baichung’s grandfather age
= 17 + 55 = 72 years
Question 12.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age ?
Solution:
Let Ravi’s present age be x years
15 years later Ravi’s age
= x + 15 years
According to the question
4x = x + 15
or, 4x – x =15
or, 3x = 15
∴ x = 5 years
Ravi’s present age = 5 years
![]()
Question 13.
A rational number is such that when you multiply it by \(\frac{5}{2}\) and add \(\frac{2}{3}\) to the product, you get \(\frac{-7}{12}\) number ?
Solution:
Let the number be x.
x is multiply by \(\frac{5}{2}\) = \(\frac{5x}{2}\) and \(\frac{2}{3}\)
∴ \(\frac{5x}{2}\) + \(\frac{2}{3}\) = \(\frac{7}{12}\)
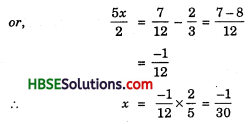
Therefore, the rational number is \(\frac{-1}{30}\).
Question 14.
Lakshmi is a cashier in a bank. She has currency notes of denominations Rs. 100, Rs. 50 and Rs. 10, respectively. The ratio of the number of these notes is 2:3:5. The total cash with Lakshmi is Rs. 4,00,000. How many notes of each denomination does she have ?
Solution:
Let the ratio be x
Number of Rs. 100 notes
= 2x
Value = Rs. 100 × 2x
= Rs. 200x
Number of Rs. 50 notes
= 3x
Value = Rs. 100 × \(\frac{3x}{2}\)
= Rs. 150x
(∵ Rs.50 notes = 3x, Rs. 100 notes = \(\frac{3x}{2}\))
Number of Rs. 10 notes = 5x
Value = Rs 100 × \(\frac{5x}{10}\) = 50x
According to the question
200x + 150x + 50x = 4,00,000
or, 400x = 4,00,000
x = 1000
Number of Rs. 100 notes
= 2 × 1000 = 2000
Number of Rs. 50 notes
= 3 × 1000 = 3000
Number of Rs. 10 notes
= 5 × 1000 = 5000
![]()
Question 15.
I have a total of Rs. 300 in coins of denomination Re. 1, Rs. 2 and Rs. 5. The number of Rs. 2 coins is 3 times the number of Rs. 5 coins. The total number of coins is 160. How many coins of each denomination are with me ?
Solution:
The total number of coins = 160
Let the number of Re. 1 coins be x
Value = Rs. x
Number of Rs. 5 coins be y (let)
Value = Rs. 5y
Number of Rs. 2 coins
= 3y
Value = Rs. 6y
∴ x + y + 3y = 160
x + 5y + 6y = 300
or, x + 4y = 160 …(i)
and x + lly = 300 … (ii)
Subtract (i) from (ii)
we get 7y = 140
y = 20
From (i) x + 4 × 20 = 160
x + 80 = 160
x = 160 – 80 = 80
Number of Re. 1 coins = 80
Number of Rs. 5 coins = 20
Number of Rs. 2 coins
= 3 × 20 = 60
Question 16.
The organisers of an essay competition decide that a winner in the competition gets a prize of Rs. 100 and a participant who does not win gets a prize of Rs. 25. The total prize money distributed is Rs. 3,000. Find the number of winners, if the total number of participants is 63.
Solution:
The total number of participants is 63.
Let the number of winner be x.
Winners get Rs. 100 x
Number of participants who does not win = 63 – x
They get Rs. (63 – x) × 25
According to the question
100x + (63 – x) × 35
= 3000
or, 100x + 1575 – 25x = 3000
or, 75x + 1575 = 3000
or, 75x = 3000-1575
or, 75x = 1425
or, x = \(\frac{1425}{75}\) ∴ 19
∴ Number of winners = 19