Haryana State Board HBSE 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.3 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals Exercise 3.3
Question 1.
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
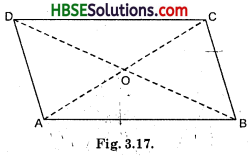
(i) AD = ……….
(ii) ∠DCB = ………..
(iii) OC = ………….
(iv) m ∠DAB + m ∠CDA = …………
Solution:
(i) AD = BC [Opposite sides are equal]
(ii) ∠DCB = ∠DAB
[Opposite angles are equal]
(iii) OC = OA [Diagonals bisect each other]
(iv) m∠DAB + m∠CDA = 180°.
[Interior opposite angles-since \(\overline{\mathrm{AB}}\) || DC]
Question 2.
Consider the following parallelograms. Find the values of the unknowns x, y, z.
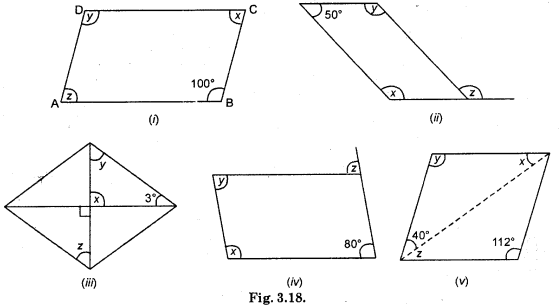
Solution:
(i) ∠D = ∠B
[Opposite angles are equal]
∴ y = 100°
[∵ ∠B = 100°]
In ||gm ABCD,
∠A + ∠B + ∠C + ∠D = 360°
∠z + 100° + ∠x + 100° = 360°
∠z + ∠x + 200 = 360°
∴ ∠z + ∠x = 360 – 200 = 160°
But, ∠z = ∠x
[Opposite angles are equal]
2∠z = 160°
∴ ∠z = 80° = ∠x
Hence, ∠A = z = 80°, ∠B = 100°, ∠C = x = 80°, ∠D = y= 100°.
(ii) ABCD is a parallelogram
∴ ∠D = ∠ABC
[Opposite angles are equal]
∴ ∠ABC = 50°
∠ABC + ∠CBP = 180° [Linear pair]
50° + ∠CBP = 180°
∴ ∠CBP = 180° – 50° = 130°
∴ ∠CBP = ∠ = 130°
In ||gm ABCD,
∠A + ∠B + ∠C + ∠D = 360°
x + 50° + y + 50° = 360°
x + y + 100° = 360°
x + y = 360° – 100° = 260°
But, ∠x = ∠y
[Opposite angles are equal]
2∠x = 260°
∴ ∠x = 130° = ∠y
Hence, ∠x = 130°; ∠z = 130°; ∠y = 130°.
(iii) ∠AOD = ∠BOC
Here, ∠BOC = 90°
∴ ∠AOD = 90°
In △AOD,
∠AOD + ∠ADO + ∠OAD = 180°
[Angle sum property]
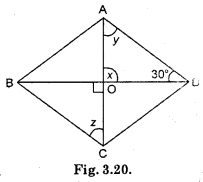
90° + 30° + ∠OAD = 180°
120° + ∠OAD = 180°
∴ ∠OAD = 180° – 120° = 60°
∴ ∠OAD = ∠y = 60°
∠y = ∠z
[∵ AD || CD] (alt. int. angle]
∴ ∠z = 60°.
(iv) ABCD is a ||gm
∴ ∠B = ∠D
∴ ∠y = 80° [∵ ∠D = y]
∠B = ∠z
[Corresponding angles since AB || BP]
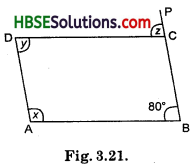
∴ ∠z = 80°
∠z + ∠BCD = 180° [Linear pair]
80° + ∠BCD = 180°
∴ ∠BCD = 180° – 80° = 100°
∠BCD = ∠x [Opposite angles are equal]
∴ ∠x = 100°
Hence, ∠x = 100°, ∠z = 80°, ∠y = 80°.
(v) ∠B = ∠D
[Opposite angles are equal]
∴ ∠D = 112°
InABCD, ∠A + ∠B + ∠C + ∠D = 360°
or ∠A + 112° + ∠C + 112° = 360°
or ∠A + ∠C + 2240 = 360°
or ∠A + ∠C = 360° – 224°
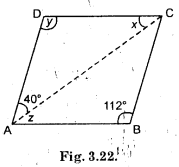
or ∠A + ∠C = 136°
But ∠A = ∠C
∴ 2∠A = 136°
∠A = 68°
∴ ∠A = ∠C = 68°
∠A = 40°+ z
68° = 40° + z
∴ ∠ = 68° – 40° = 28°
∴ ∠z = ∠x = 28° [Alternative angles]
Hence, x = 28°, y = 112°, ∠z = 28°.

Question 3.
Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180° ?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm ?
(iii) ∠A = 70° and ∠C = 65° ?
Solution:
(i) Can be, but need not be, because sum of opposite angles of a rectangle and a square is 180°, but it need not be a parallelogram, rhombus.
(ii) No, here AB = CD, but AD ≠ BC, because in a parallelogram opposite sides are equal.
(iii) No, in a parallelogram opposite angles are equal, here ∠A ≠ ∠C.
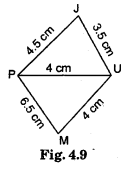
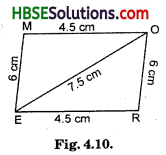
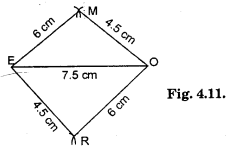
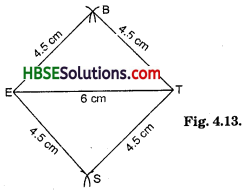
Question 4.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
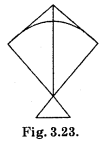
Solution:
A kite, for example
Let ∠B = ∠D = x [Opposite angles property]
In parallelogram ABCD,
∠A + ∠B + ∠C + ∠D = 360°
75° + x + 75° + x = 360°
or 2x +150° = 360°
or 2x = 360°-150° = 210°
x = 105°
Hence, ∠A = 75°, ∠B = 105°, ∠C = 75° and ∠D = 105°.

Question 5.
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution:
Given: ABCD is a parallelogram, ∠A and ∠B are in the ratio of 3 : 2.
Find ∠A, ∠B, ∠C and ∠D.
Let the ratio = x
∴ ∠A = 3x, ∠B = 2x
∠A + ∠B = 180° [Sum of interior angles]
or 3x + 2x = 180°
or 5x = 180°
∴ x = 36°
∠A = 3 × 36° = 108°
∠B = 2 × 36° = 72°
∠A = ∠C = 108°
∠B = ∠D = 72°.
Question 6.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Solution:
Given : ∠A = ∠B = x let
∠A + ∠B = 180°
[Sum of interior angles]
∵ AD | | BC
x + x = 180°
2x = 180°
∴ x = 90°

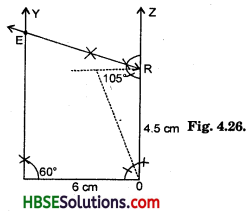
Question 7.
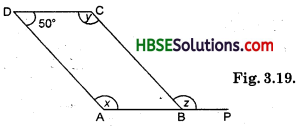
The adjacent figure HOPE is a paralieogram. Find the angle measures x, y and z. State the properties you use to find them.
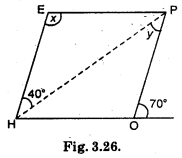
Solution:
70° + ∠POH = 180° [Linear pair]
∴ ∠POH = 180° -70°
∴ ∠POH = 110°
∠POH = ∠HEP
[Opposite angles of a parallelogram HOPE]
∴ x = 110°
∠EHP = ∠HPO
[Alternative interior angles]
∴ ∠y = 40°.
Question 8.
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
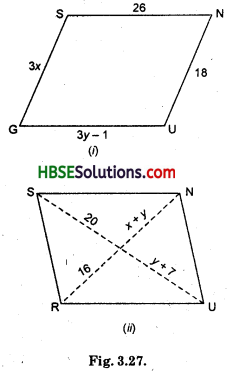
Solution:
(i) GUNS is a parallelogram
∴ GU = SN
[Opposite sides of a ||gm]
or 3y – 1 = 26
3y = 26 + 1
3y = 27
∴ y = \(\frac{27}{3}\) = 9
GS = UN
[Opposite sides of a ||gm]
3x = 18
∴ x = 6
Therefore, x = 6, y = 9.
(ii) y + 7 = 20
y = 20 – 7 = 13
∴ y = 13
x + y = 16
[Diagonals of a ||gm bisect each other]
or x + 3 = 16
∴ x = 16 – 13 = 3
Therefore, x = 3, y = 13.

Question 9.
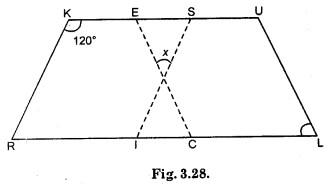
In the figure both RISK and CLUE are parallelogram. Find the value of x.
Solution:
RISK is a ||gm
∴ ∠K = ∠RIS = 120°
In ||gm RISK,
∠KRI = ∠ISK = x (let)
∠SKR + ∠KRI + ∠RIS + ∠ISK = 360°
or 120° + x + 120° + x = 360°
or 240° + 2x = 360°
or 2x = 360° – 240°
= 120°
x = \(\frac{120}{2}\) = 60°
∴ ∠ISK = 60°
CLUE is a ||gm
∴ ∠L = ∠CEU = 70
In triangle shape,
∠x + ∠CEU + ∠ISK = ∠x + ∠S + ∠E
= 180°
x + 70° + 60°
= 180°[∵ ∠x = 50°]
∴ x = 180° – 70° – 60°
= 50°.
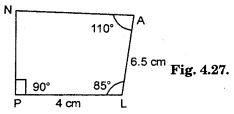
Question 10.
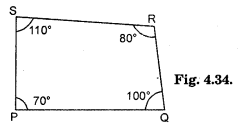
Explain how this figure is a trapezium. Which of its two sides are parallel ? (Fig. 3.29)
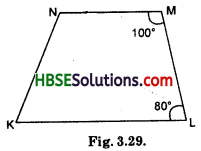
Solution:
∠KLM + ∠NML = 80° + 100° = 180° [Sum of interior opposite angles 180°]
∴ \(\overline{\mathrm{NM}}\) || \(\overline{\mathrm{KL}}\). So KLMN is a trapezium.

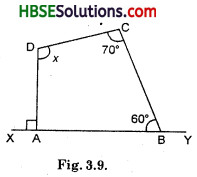
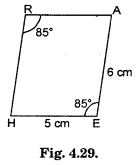
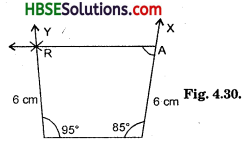
Question 11.
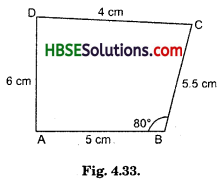
Find m∠C in Fig. 3.30, if \(\overline{\mathrm{AB}}\). \(\overline{\mathrm{DC}}\).
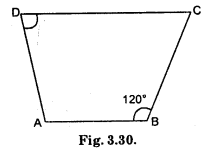
Solution:
∠B + ∠C = 180°
120°+ ∠C = 180°
∴ ∠C = 180° – 120° = 60° ^
∴ ∠C = 60°.
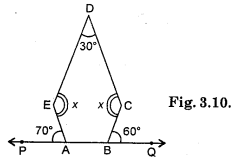
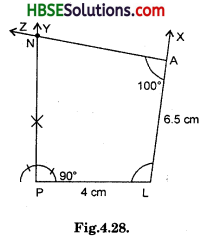
Question 12.
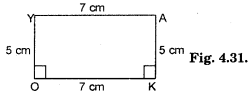
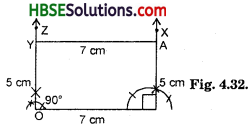
Find the measure of ∠P and ∠S if \(\overline{\mathrm{SP}}\).\(\overline{\mathrm{RQ}}\) in Fig. 3.31. (If you find m∠R, is there more than one method to find m∠P)?
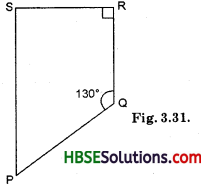
Solution:
∠QRS + ∠RSP = ,180°
[Sum of interior opposite angle is 180° because \(\overline{\mathrm{SP}}\).\(\overline{\mathrm{RQ}}\)]
90° + ∠RSP = 180°
∴ ∠RSP = 90°
In quad. PQRS,
∠P + ∠Q + ∠R + ∠S = 360°
∠P + 130° + 90° + 90° = 360°
or ∠P + 310° = 360°
∴ ∠P = 360° – 310° = 50°
∴ ∠P = 50°; ∠S = 90°
![]()
![]()