Haryana State Board HBSE 8th Class Maths Solutions Chapter 4 Practical Geometry InText Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 4 Practical Geometry InText Questions
Think, Discuss and Write (Page-58)
Question 1.
Arshad has five measurements of a quadrilateral ABCD. These are AB = 5 cm, ∠A = 50°, AC = 4 cm, BD = 5 cm and AD = 6 cm. Can he construct a unique quadrilateral? Give reasons for your answer.
Solution:
No, he cannot construct a quadrilateral because side BC or DC are not given. Although five measurements are given yet they are not sufficient to construct a quadrilateral.
Think, Discuss and Write (Page-60)
Question 1.
(i) We saw that 5 measurements of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurements of the quadrilateral can do this?
(ii) Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and AS = 6.5 cm? Why?
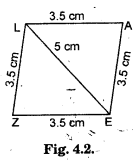
(iii) Can you draw a rhombus ZEAL where ZE = 3.5 cm, diagonal EL = 5 cm? Why?
(iv) A student attempted to draw a quadrilateral PLAY where PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm, but could not draw it. What is the reason?
[Hint: Discuss it using a rogh sketch.]
Solution:

(i) No, It should be in a specific manner.
(ii) Yes, because opposite sides of a parallelogram are equal.
∴ BA = ST = 5 cm.
AT = BS = 6 cm.
and one diagonal AS = 6.5 is given
(iii) Yes, because all sides of a rhombus are equal.
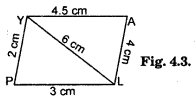
(iv) PL + PY = 2 + 3 = 5 cm.
YL = 6 cm. ,
∴ PL + PY < YL
Sum of two sides in a A must be greater than the 3rd side.
![]()
Think, Discuss and Write (Page-62)
Question 1.
In the above example 2 (NCERT) , can we draw the quadrilateral by drawing △ABD first and then find the fourth point C?
Solution:
1. No, because the length of AB is not given.
Question 2.
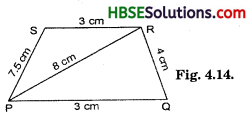
Can you construct a quadrilateral PQRS with PQ = 3 cm, RS = 3cm, PS = 7.5 cm, PR = 8 cm and SQ = 4cm? Justify your answer.
Solution:
No, because sum of two sides in a △ must be greater than the 3rd side
In △ SPR
Here, PS + SR = 7.5 cm + 3 cm = 10.5cm.
and PR = 8 cm.
So, PS + SR > PR
But In △PQR, PQ + QR = 3 + 4 = 7 cm.
and PR = 8 cm.
∴ PQ + QR < PR.
![]()
Think, Discuss and Write (Page-64)
Question 1.
1. Can you construct the above quadrilateral MIST if we have 100° at M instead of 75°?
2. Can you construct the quadrilateral PLAN if PL m 6 cm, ∠A = 9.5 cm, ∠P = 75°, ∠L = 150° and ∠A = 140°? (Hint: Recall angle-sum property).
3. In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct as in the example above ?
Solution:
1. Sum of all angles of a quadrilateral 100° + 105° + 120° + x = 360°
⇒ 325° + x = 360°
⇒ x = 360° – 325 ° = 35°.
∴ Quadrilateral MIST is possible to construct.

2. ∠P + ∠L + ∠A = 365°
75° + 150° + 140° = 365°
Sum of four angles in a quadrilateral is 360°.
∴ Quadrilateral is not possible to construct.
3. No, it is not required to have the measure of angles because opposite sides of a parallelogram are equal.
If AB = BC .
then, AB = DC, BC = AD.
Think, Discuss and Write (Page-66)
Question 1.
1. In the example 4 (NCERT), we first drew BC. Instead, what could have been be the other starting points ?
2. We used some five measurements to draw quadrilaterals so far. Can there be different sets of five measurements (other than seen so far) to draw a quadrilateral ?
The following problems may help you in answering the question :
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and ∠B = 80°.
(ii) Quadrilateral PQRS with PQ = 4.5 cm, ∠P = 70°, ∠Q = 100°, ∠R = 80° and ∠S = 110°.
Solution:
You can start with drawing CD = 6.5 cm and make ∠C = 80° and cut off BC = 5 cm and then make ∠B = 105°.
(2) (i) Rough Sketch :
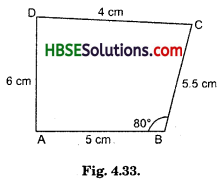
We can construct a quadrilateral ABCD with four sides and one angle.
(ii) Rough Sketch :
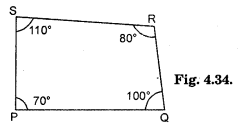
Here, at least one side RQ or PS in required. So, data is in sufficient.
You may construct if
(i) Two angles and two sides, e.g. if ∠A = 90, ∠B = 80, AD = 6 cm BC = 5 cm.
(ii) Four angle and two sides e.g. PQ = 4.5 cm, ∠P = 65°, ∠Q = 110°,
∠QR = 4.7 cm, ∠R = 115°.
![]()
Think, Discuss and Write (Page-67)
Question 1.
1. How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
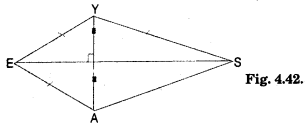
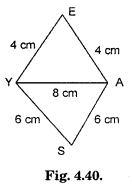
2. Construct the kite EASY if AY = 8 cm, EY = 4 cm and SY = 6 cm (Fig.). Which properties of the kite did you use in the process?
Solution:
1. We know that opposite sides of a rectangle are equal and each angle is 90°.
∴ If PQ and QR are given, then we have PQ = RS and QR = PS
∠P = ∠Q = ∠R = ∠S = 90°.
Which is sufficient to construct a rectangle PQRS
(2) Rough Sketch:
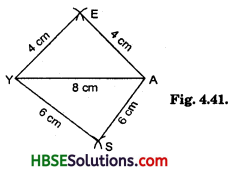
A kite has two isosceles triangles with common base.
i.e. EY = EA and YS = AS.
Steps of Construction:
(i) Draw YA = 8 cm
(ii) Take arcs of 4 cm with centre as Y and A respectively.
(iii) Let these arcs intersect at E.
(iv) Similarly, on the opposite side of YA take two arcs YS = SA = 6 cm and obtain the point S.
(v) Join EY, EA, YS and AS.
(vi) You have a required kite EASY.
Second Method : You can draw perpendicular bisector of YA and cut off EY = 4 cm and YS = 6 cm.