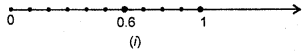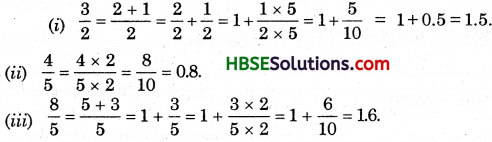Author name: Prasanna

Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 Fractions Intext Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 7 Fractions Intext Questions

Try These (Page 175):

Question 1.
Show \(\frac{3}{5}\) on a number line.
Solution:

We divide the gap between 0 and 1 into 5 equal parts. \(\frac{3}{5}\) means 3 parts out of 5 parts as shown above.

Question 2.
Show \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) and \(\frac{10}{10}\) on a number line.
Solution:

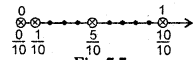
We divide the gap between 0 and 1 into 10 equal parts. \(\frac{1}{10}\) means 1 part out of 10 parts as shown above.
\(\frac{0}{10}\) is the point zero whereas \(\frac{10}{10}\) is 1 whole, which can be shown by the points 0 and 1 respectively (as shown in Fig.).
Now, \(\frac{5}{10}\) means 5 parts out of 10 parts as shown in the Fig.

Question 3.
Can you show any other fraction between 0 and 1 ? Write 5 more fractions that you can show and depict them on the number line.
Solution:
Yes, we can show other fractions between 0 and 1
e.g., \(\frac{1}{8}, \frac{3}{8}, \frac{4}{8}, \frac{5}{8}, \frac{7}{8}\) are five more fractions between 0 and 1.

Question 4.
How many fractions are there between 0 and 1 ? Think, discuss and write you answer.
Solution:
There are an infinite number of fractions between 0 and 1.

Try These (Page 175):

Question 1.
Give a proper fraction :
(a) The numerator of which is 5 and denominator is 7.
(b) The denominator of which is 9 and numerator is 5.
(c) The numerator and denominator of which add. up to 10. How many frac¬tions of this kind, can you make ?
(d) The denominator of which is 4 more than the numerator. (Make any 5, how many more can you make ?)
Solution:
(a) \(\frac{5}{7}\)
(b) \(\frac{5}{9}\)
(c) \(\frac{1}{9}, \frac{2}{8}, \frac{3}{7}, \frac{4}{6}\) are four proper fractions of this kind.
(d) \(\frac{1}{5}, \frac{2}{6}, \frac{3}{7}, \frac{4}{8}, \frac{5}{9}\)
We can make an infinite number of such proper fractions.

Question 2.
A fraction is given.
How will you decide, by just looking at it, whether, the fraction is :
(a) Less than 1 ? (b) Equal to 1 ?
Solution:
(a) If numerator is less than the denominator, then the fracton is less than 1.
(b) If numerator is equal to the denominator, then the fraction is equal to 1.

Question 3.
Fill up, using one of these : ‘>\ ‘<’ or ‘=’.

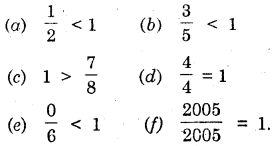
Solution:

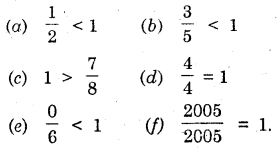
Try These (Page 177):

Question.
(a)Write 5 improper fractions with denominator 7 ?
(b) Write 5 improper fractions with numerator 11 ?
Solution:
(a) \(\frac{8}{7}, \frac{11}{7}, \frac{15}{7}, \frac{20}{7}, \frac{30}{7}\)
(b) \(\frac{11}{5}, \frac{11}{6}, \frac{11}{7}, \frac{11}{8}, \frac{11}{9}\)
Is the fraction \(\frac{11}{11}\) proper or improper ?
Answer:
\(\frac{11}{11}\) is an improper fraction.

Try These (Page 181)

Question 1.
Are \(\frac{1}{3}\) and \(\frac{2}{6}\) equivalent ? Give reason.
Solution:
Yes, because \(\frac{1}{3}=\frac{1 \times 2}{3 \times 2}=\frac{2}{6}\)

Question 2.
Are \(\frac{2}{5}\) and \(\frac{2}{7}\) equivalent ? Give reason.
Solution:
No, because \(\frac{2}{5} \neq \frac{2}{7}\)

Question 3.
Are \(\frac{2}{9}\) and \(\frac{6}{27}\) equivalent ? Give reason.
Solution:
Yes, because \(\frac{2}{9}=\frac{2 \times 3}{9 \times 3}=\frac{6}{27}\)

Question 4.
Give another example of 4 equivalent fractions.
Solution:
\(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}, \frac{36}{72}\) -are all equivalent fractions.

Question 5.
Identify the fractions in each. Write down which fractions are equivalent ?

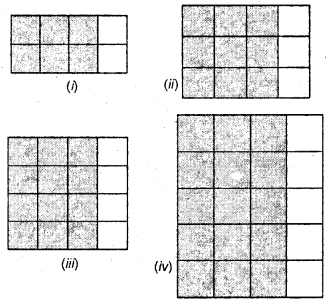
Solution:


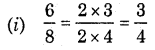
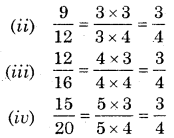
We see that all fractions are all equal. Hence, all fractions are equivalent.

Try These (Page 183) :

(a) Find five equivalent fractions of each :
(i) \(\)
(ii) \(\)
(iii) \(\)
(iv) \(\)
Solution:

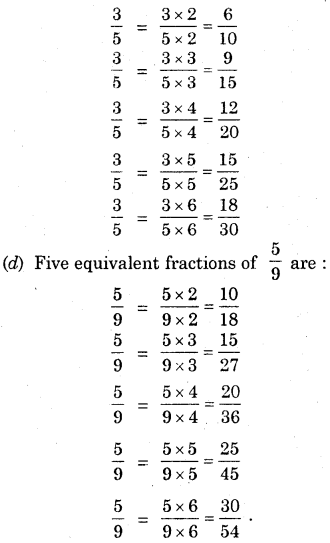
Try These (Page 187):

Question.
(a) Write the simplest form of
(i) \(\frac{15}{75}\)
(ii) \(\frac{16}{72}\)
(iii) \(\frac{17}{51}\)
(iv) \(\frac{42}{28}\)
(v) \(\frac{80}{24}\)
(b) Is \(\frac{169}{289}\) in its simplest form ?
Solution:
(a) (i) Factors of 15 are : 1, 3, 5, 15
Factors of 75 are : 1, 3, 5, 15, 25, 75
Common factors are : 1, 3, 5, 15
∴ The HCF of 15 and 75 is 15.
Now, \(\frac{15}{75}=\frac{15 \div 15}{75 \div 15}=\frac{1}{5}\)

(ii) Factors of 16 are : 1, 2, 4, 8, 16
Factors of 72 are : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Common factors are : 1, 2, 4, 8.
∴ The HCF of 16 and 72 is 8.
Now, \(\frac{16}{72}=\frac{16 \div 8}{72 \div 8}=\frac{2}{9}\)

(iii) Factors of 17 are : 1, 17
Factors of 51 are : 1, 3, 17, 51
Common factors are : 1, 17
∴ The HCF of 17 and 51 is 17.
Now, \(\frac{17}{51}=\frac{17 \div 17}{51 \div 17}=\frac{1}{3}\)

(iv) Factors of 42 are : 1, 2, 3, 6, 7, 14, 21, 42
Factors of 28 are : 1, 2, 4, 7, 14, 28.
Common factors are : 1, 2, 7, 14.
∴ HCF of 42 and 28 is 14.
Now, \(\frac{42}{28}=\frac{42 \div 14}{28 \div 14}=\frac{3}{2}\)

(v) Factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80.
Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24.
Common factors are: 1, 2, 4, 8
∴ HCF of 80 and 24 is 8.
Now, \(\frac{80}{24}=\frac{80 \div 8}{24 \div 8}=\frac{10}{3}\)

(b) ∵ HCF of 169 and 289 is 1.

Try These (Page 191):

Question 1.
You get one fifth of a bottle of juice and your sister gets one-third of a bottle of juice. Who gets more ?
Solution:
One fifth of a bottle of juice = \(\frac{1}{5}\)
One third of a bottle of juice = \(\frac{1}{3}\)
Comparing \(\frac{1}{5}\) and \(\frac{1}{3}\), we find that \(\frac{1}{3}>\frac{1}{5}\)
Thus, your sister gets more juice.

Try These (Page 191):

Question 1.
Which is the larger fraction :
(i) \(\frac{7}{10} \text { or } \frac{8}{10}\)
(ii) \(\frac{11}{24} \text { or } \frac{13}{24}\)
(iii) \(\frac{17}{102} \text { or } \frac{12}{102}\)
Why are these comparisons easy to make ?
Solution:
(i) \(\frac{8}{10}\) is larger than \(\frac{7}{10}\)
(ii) \(\frac{13}{24}\) is larger than \(\frac{17}{102}\)
(iii) \(\frac{12}{102}\) larger than \(\frac{17}{102}\)
These comparisons are easy to make, because their denominators are same.

Question 2.
Write these in ascending and also in descending order :
(a) \(\frac{1}{8}, \frac{3}{8}, \frac{5}{8}, \frac{11}{8}, \frac{13}{8}\)
(b) \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}, \frac{7}{5}, \frac{11}{5}\)
(c) \(\frac{1}{7}, \frac{3}{7}, \frac{2}{7}, \frac{11}{7}, \frac{13}{7}, \frac{15}{7}\)
Solution:

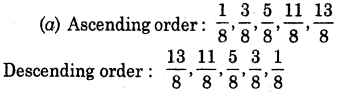
Try These (Page 193) :

Question 1.
Arrange the following in ascending and descending order:
(a) \(\frac{1}{12}, \frac{1}{23}, \frac{1}{5}, \frac{1}{7}, \frac{1}{50}, \frac{1}{9}, \frac{1}{17}\)
(b) \(\frac{3}{7}, \frac{3}{11}, \frac{3}{5}, \frac{3}{2}, \frac{3}{13}, \frac{3}{4}, \frac{3}{17}\)
(c) Write 3 more similar examples and arrange them in ascending and descending order.
Solution:

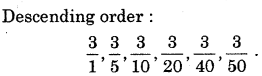
Try These (Page 198) :

Question 1.
My mother divided the apple into 4 equal parts. She gave me two parts and my brother one part. How much apple did she give both of us together ?
Solution:
Apple given to me = \(\frac{2}{4}\)
Apple given to my brother = \(\frac{1}{4}\)
∴ Apple given to both of us together = \(\frac{2}{4}+\frac{1}{4}\)
= \(\frac{2+1}{4}=\frac{3}{4}\)

Question 2.
The mother asked Neelu and her brother to pick stones from the wheat Neelu picked 1/4th of the total stones in it and her brother also picked up l/4th of the stones. How many stones both picked up together ?
Solution:
Stones picked up by Neelu
= 1/4th of the total stones
Stones picked up by her brother
= 1/4th of the total stones
∴ Stones picked up by both together
= \(\frac{1}{4}+\frac{1}{4}\)
= \(\frac{1+1}{4}=\frac{2}{4}\)
= \(\frac{1}{2}\) of the total stones.

Question 3.
Sohan was making a table. He made l/4th of the table by Monday. He made another l/4th on Tuesday and Wednesday. How much of the table has been made by Wednesday evening ?
Solution:
Table made on Monday = \(\frac{1}{4}\)
Table made on Tuesday & Wednesday = \(\frac{1}{4}\)
∴ Table made by Wednesday evening = \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

Try These (Page 200) :

Question 1.
Add, with the help of a diagram :
(i) \(\frac{1}{8}+\frac{1}{8}\)
(ii) \(\frac{2}{5}+\frac{3}{5}\)
(iii) \(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}\)
Solution:

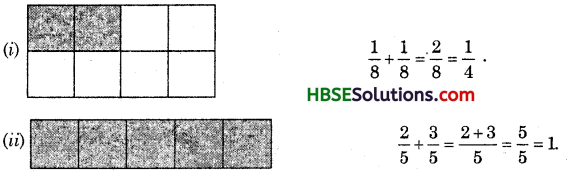
Question 2.
What do we get when we do this \(\)?
Solution:
\(\frac{2}{5}+\frac{4}{5} ?\)
By Pictorially:

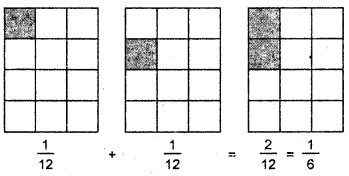
Using paper folding: Take a square piece of paper. Fold it by overlapping its edge AB and CD to get

Again. refold it by taking
EF over C(A) D(B). Reopen it.

Now fold is vertically at two places to obtain three equal vertical portion as shown.
Shade \(\frac{1}{12}\) portion two times.
Now, we see \(\frac{1}{12}+\frac{1}{12}=\frac{2}{12}=\frac{1}{6}\)

Question 3.
Make 10 more examples of problems given in 1 and 2 above. Solve them with your friends.
Solution:

Try These (Page 201):

Question 1.
Find the difference between \(\frac{7}{4}\) and \(\frac{3}{4}\).
Solution:
\(\frac{7}{4}-\frac{3}{4}=\frac{7-3}{4}=\frac{4}{4}=1\)

Question 2.
Mother made a gud patti in a round shape. She divided it into 5 equal pieces. Seema ate one piece from it. If I ate another piece, how much was be left ?
Solution:
Gud patti in a round shape has been divided into 5 equal parts.
Each part = \(\frac{1}{5}\)
Seema ate one piece from it i.e., \(\frac{1}{5}\)
I ate another piece from it i.e.,\(\frac{1}{5}\)
Gud patti eaten by both of us = \(\frac{1}{5}+\frac{1}{5}=\frac{2}{5}\)
Part of gud patti left = \(1-\frac{2}{5}=\frac{5-2}{5}=\frac{3}{5}\)

Question 3.
My elder sister divided the water melon into 18 parts. I ate 7 out of them. My friend ate 4. How much did we eat ? How much more of water melon did I eat compared to my friend ? What amount of water melon remains ?
Solution:
Water melon is divided into 18 parts,.
∴ Each part = \(\frac{1}{18}\)
I ate 7 out of them i.e., \(\frac{7}{18}\)
My friend ate 4 out of them i.e., \(\frac{4}{18}\)
Water melon eaten by both of us = \(\frac{7}{18}+\frac{4}{18}=\frac{7+4}{18}=\frac{11}{18}\)
Difference between the two =\(\frac{7}{18}+\frac{4}{18}=\frac{7-4}{18}=\frac{3}{18}=\frac{1}{16}\)
I ate \(\frac{1}{6}\) more water melon as compared to my friend.
Amount of water melon remains =\(1-\frac{11}{18}=\frac{18-11}{18}=\frac{7}{18}\)

Question 4.
Make 5 problems of this type and solve them with friends.
(i) My mother divided the apple into 4 equal parts. She gave me 2 parts and my brother one part. How much apple was left ?
(ii) The mother asked Neelu and her brother to pick up stones from the wheat. Neelu picked up 1/4th of the total stones in it and her brother also picked up 1/4th of the stones. How many stones were left ?
(iii) Sohan was making a table. He made 1/4th of the table on Monday. He made another 1 /4th on Tuesday and Wednesday. How much table was left to be built ?
(iv) Sharmilahad \(\frac{5}{6}\) of a cake. She gave \(\frac{2}{6}\) out of that to her younger b
brother. How much cake is left with her ?
(v) My elder brother divided the water melon into 10 equal parts. He ate 8 out of them and gave me 2. How much more of water melon did he eat compared to me ? How much did we eat together ? What amount of water melon remains ?
Solution:
(i) Apple given to me = \(\frac{2}{4}\), apple given to my brother = \(\frac{1}{4}\)

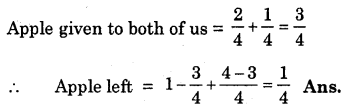
(ii) Stones picked up by Neelu = \(\frac{1}{4}\)
Stones picked up by her brother = \(\frac{1}{4}\)
∴ Stones picked up by both

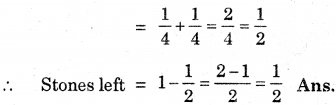
(iii) Table made on Monday = \(\frac{1}{4}\)
Table made on Tuesday and Wednesday = \(\frac{1}{4}\)
∴ Table made by Wednesday evening = \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)
∴ Table left to be made
= \(1-\frac{1}{2}=\frac{2-1}{2}=\frac{1}{2}\)

(iv) Sharmila had 5/6 of a cake and she
gave 2/6 to her brother.
Cake left with her

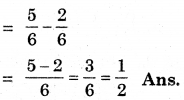
(v) Water melon is divided into 10 equal parts.
∴ Eachpart = \(\frac{1}{10}\)
My brother ate 8 out of them i.e., \(\frac{8}{10}\)
He gave me 2 out of 10 i.e., \(\frac{2}{10}\)
Difference between the two \([latex]\frac{8}{10}-\frac{2}{10}=\frac{8-2}{10}=\frac{6}{10}=\frac{3}{5}\)[/latex]
My brother ate \(\frac{3}{5}\) more water melon as compared to me.
Water melon eaten by both of us together
\(\frac{8}{10}+\frac{2}{10}=\frac{8+2}{10}=\frac{10}{10}=1\)
Amount of water melon remains = 1 – 1 = 0
i.e., the whole water melon is eaten by us.

Try These (Page 204)

Question 1.
Add \(\frac{2}{5}\) and \(\frac{3}{7}\)
Solution:
\(\frac{2}{5}+\frac{3}{7}\) We have L.C.M. (5, 7) = 35
\(\frac{2 \times 7+5 \times 3}{35}\)
[We have done this to find equivalent fractions]
\(\frac{14+15}{35}=\frac{29}{35}\)

Question 2.
Subtract \(\frac{2}{5}\) from \(\frac{5}{7}\)
Solution:
\(\frac{5}{7}-\frac{2}{5}\)
We have L.C.M. (7, 5) = 35
\(\frac{5 \times 5-7 \times 2}{35}\)
[We have done this to find equivalent fractions]
\(\frac{25-14}{35}\)
\(\frac{11}{5}\)

Try These (Page 206) :

Question.
(i) 2\(\frac{1}{5}\) and 3\(\frac{2}{6}\)
(ii) 2\(\frac{2}{3}\) from 5\(\frac{6}{7}\)
Solution:

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.5

Try These (Page 211) :

Question 1.
Can you now write the following numbers as decimals ?

Solution:
(i) 538.1,
(ii) 273.4,
(iii) 354.6.

Question 2.
Write the lengths of Ravi’s and Raju’s pencils in cm using decimals.
Solution:
Length of Ravi’s pencil
= 7 cm 5 mm = 7.5 cm.
Length of Raju’s pencil
= 8 cm 3 mm = 8.3 cm.

Question 3.
Make three more examples similar to the one given in question 1 and solve them.
Solution:
(i) Ram has rupees 40 and seventy-five paise and Shyam has rupees 70 and fifty paise. Express these amounts in decimal fractions.
(ii) The length of a wire is 6 metre and 30 cm. Write this length of wire in metres.
(iii) Pallavi and Ashu measured the lengths of their pencils. Pallavi’s pencil was 6 cm and 4 mm long and Ashu’s pencil was 5 cm 7 mm. Write the lengths of their pencils in cm.
Solution:
(i) Rs. 40 and seventy five paise
= Rs. 40.75
Rs. 70 and fifty paise
= Rs. 70.50

(ii) The length of the wire
= 6 metre and 30 cm = 6.30 m.

(iii) Length of Pallavi’s pencil
= 6 cm and 4 mm = 6.4 cm.
Length of Ashu’s pencil
= 5 cm and 7 mm = 5.7 cm.

Try These (Page 212):

Question.
Represent the following numbers on the number line :
(i) 0.6, (ii) 1.2, (Hi) 2.3.
Solution:
(i) We know that 0.6 is more than zero but less than one. There are 6 tenths in it. Divide the unit length between 0 and 1 into 10 equal parts and take 6 parts as shown below:

(ii) We know that 1.2 is more than one but less than two. There are 2 lengths in it. Divide the unit length between 1 and 2 into 10 the equal parts and take 2 parts as shown below :

(iii) We know that 1.2 is more than one but less than two. There are 2 lengths in it. Divide the unit length between 1 and 2 into 10 the equal parts and take 2 parts as shown below :

Try These (Page 213) :

Question.
Write \(\frac{3}{2}, \frac{4}{5}, \frac{8}{5}\) in decimal notation.
Solution:

Decimals as Fractions :
Write a decimal number 1.2 as a fraction.
Solution:
1.2 = 1.2 \(=\frac{10}{10}+\frac{2}{10}=\frac{10+2}{10}=\frac{12}{10}=\frac{6}{5}\)

Try These

Question 1.
David was measuring the length of his room. He found that the length of his room is 4 m and 25 cm. He wanted to write the length in metres. Can you help him.
Solution:
4 m and 25 cm = 4 + \(\frac{25}{100}\) = 4.25 m.

Question 2.
Fill in the blanks :
Ordinary fraction Decimal fraction

Solution:
(a) 0.50,
(b) 0.92.

Question 3.
Write the number in decimal fraction:

Solution:
The number is 2 + \(\frac{4}{10}+\frac{3}{100}\) = 2 + 0.4 + 0.03 = 2.43.

Try These (Page 224) :

Question.
Compare :
(i) 1.82 and 1.823
(ii) 5.7 and 4.9
(iii) 6.05 and 6.50
(iv) 3.15 and 3.18.
Solution:

Try These (Page 225):

(i) Write 2 rupees 5 paise and 2 rupees 50 paise in decimals.
(it) Write 20 rupees 7 paise and 21 rupees 75 paise in decimals.
Solution:
(i) We know that
100 paise = 1 Re
.’. 1 paise = \(\frac{1}{100}\) Re = 0.01 Re
.’. 5 paise = \(\frac{5}{100}\) Re = 0.05 Re
Hence, 2 rupees 5 paise 2.05 Rs.
and 50 paise = \(\frac{50}{100}\) = 0.5 Re
Hence, 2 rupees 50 paise = 2.50 Rs.
(ii) We know that
100 paise = 1 Re.
1 paise = \(\frac{1}{100}\) Re = 0.01 Re
7 paise = \(\frac{7}{100}\) = 0.07 Re
Hence, 20 rupees 7 paise = 20.07 Rs. 75
75 paise = \(\frac{75}{100}\) = 0.75 Re.
Hence, 21 rupees 75 paise = Rs. 21.75.

Try These (Page 226) :

(1) Can you write 4 mm in cm using decimals ?
(2) How will you write 7 cm 5 mm in cm using decimals ?
Solution:
(1) 4mm = \(\frac{4}{10}\) cm = 0.4 cm
(2) 7 cm 5 mm = 7 + [atex]\frac{5}{10}[/latex] = 7.5 cm.

Try These (Page 227):

Question.
(a) Can you write 456 g as kg using decimals ?
(b) How will you write 2 kg 9 g in kg using decimals ?
Solution:
(a) We know that
1000 g = 1 kg.
1 kg = \(\frac{1}{1000}\) kg = 0.001 kg
Hence, 456 g = \(\frac{456}{1000}\) = 0.456 kg.

(b) We know that
1000 g = 1 kg.
1 kg = \(\frac{1}{1000}\) kg = 0.001 kg
Hence 2 kg 9 g = 2 + \(\frac{9}{1000}\)
= 2 + 0.009
= 2.009 kg.

Try These (Page 229):

Find: (i) 0.29 + 0.36
(ii) 0.7 + 0.08
(iii) 1.54 + 1.80
(iv) 2.66 + 1.85.
Solution:

Try These {Page 232):

(i) Subtract 1.85 from 5.46
(ii) Subtract 5.25 from 8.28
(iii) Subtract 0.95 from 2.29
(iv) Subtract 2.25 from 5.68.
Solution:

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.5

TRY THESE :

Question 1.
In step 2 above, what would happen if we take the length of radius to
be smaller than half the length of \(\overline{\mathrm{AB}}\) ?
Solution:
If we take the radius to be smaller than half of the length of \(\overline{\mathrm{AB}}\), the arcs will not intersect each other at two points C and D.

TRY THIS (Page 380) :

Question 1.
How will you construct a 15° angle ?
Solution:
Construct of angle an 30° as shown earlier.
Now bisect this angle. We get ∠AOD = 15° [Fig.],

TRY THESE (Page 381) :

Question 1.
How will you. construct a 150° angle ?
Solution:
Construct an angle of 120° as shown earlier.
Now ∠POQ = Straight angle – 180°
∠QOC = 120°
∠POC = 180° – 120° = 60°

Bisect ∠POC to get ∠COD = 30°
Thus, ∠QOD = ∠QOC + ∠COD = 120° + 30° = 150° which is the required angle.

TRY THESE
Question.
How will you construct a 45° angle ?
Solution:
Construct ∠QOC = 90° as shown earlier. Raw \(\overrightarrow{\mathrm{OD}}\) as the bisector of ∠QOC.
Thus, ∠QOD = 45° is the required angle.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.6 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.6

Question 1.
Draw ∠POQ measures 75° and find its line of symmetry.
Solution:
steps of Construction :
(i) Construct ∠QOA = 90° and ∠QOB = 60° as shown above.

(ii) Draw \(\overrightarrow{\mathrm{OP}}\) as the bisector of ∠AOB.
(iii) Thus, ∠POQ is the required angle of measure 75°.
(iv) Draw \(\overrightarrow{\mathrm{OR}}\) as the bisector of ∠POQ which is the required line of symmetry.

Question 2.
Draw an angle of measure 147° and construct its bisector.
Solution:
Steps of Construction :
(i) Draw a ray \(\overrightarrow{\mathrm{OA}}\).
(ii) With the help of protector construct ∠AOB = 147°.

(iii) With centre ‘O’ and a convient radius, draw an arc which intersects
the arms \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\) at P and Q respectively.
(iv) With P as centre and radius more than half of PQ, draw an arc.
(v) With Q as centre and with the same radius, draw an other arc which intersects the previous arc at R.
(vi) Join OR and produce it. Thus, \(\overrightarrow{\mathrm{OR}}\) is the required bisector of ∠AOB.

Question 3.
Draw a right-angle and construct its bisector.
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘0’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at A and B.
which intersect each other at C.
(iv) Join OC. Thus, ∠COQ is the required right-angle.
(v) With B and E as centres and radius
more than half of BE, draw two arcs which intersect each other at the point D.

(vi) Join OD. Thus, \(\overrightarrow{\mathrm{OD}}\) is the required bisector of ∠COQ.

Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Solution:
Steps of Construction :
(i) Draw a ray \(\overrightarrow{\mathrm{OA}}\) .
(ii) At 0, with the help of a protector, construct ∠AOB = 153°.
(iii) Draw \(\overrightarrow{\mathrm{OC}}\) as the bisector of ∠AOB.
(iv) Again, draw \(\overrightarrow{\mathrm{OD}}\) as the bisector of ∠AOC.
(v) Again, draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠BOC.

Thus \(\overrightarrow{\mathrm{OD}}\), \(\overrightarrow{\mathrm{OC}}\) and \(\overrightarrow{\mathrm{OE}}\) divide ∠AOB into four equal parts.

Question 5.
Construct with ruler and compasses angles of following measures:
(a) 60°,
(b) 30°,
(c) 90°,
(d) 120°,
(e) 450,
(f) 135°.
Solution:

(a) ∠AOB = 60° (b) ∠AOC = 30°
(c) ∠QOC = 90° (d) ∠AOD = 120°
(e) ∠AOC = 45° (/) ∠AOC = 135°.

Question 6.
Draw an angle of measure 45° and bisect it. What is the measure of each angle you obtain ?
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘O’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at two points A and B.

(iii) With A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(iv) Join OC. Then ∠COQ is an angle of 90°.
(v) Draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠COE. Thus, ∠QOE = 45°.
(vi) Now, draw OG as the bisector of ∠QOE. Thus, ∠QOG = ∠EOG = 22\(\frac{1}{2}\)°

Question 7.
Draw an angle of measure 135° and bisect it. What is the measure of each angle you obtain ?
Solution:
Steps of Construction :
(i) Draw a line PQ and take a point ‘O’ on it.
(ii) With ‘O’ as centre and a convient radius, draw an arc which intersects PQ at A.and B.

(iii) With A and B as centres and radius more than half of AB, draw two arcs which intersect each other at R.
(iv) Join OR. Then, ∠QOR = ∠POR = 90°.
(v) Draw \(\overrightarrow{\mathrm{OD}}\) as the bisector of ∠POR. Then, ∠QOD is the required angle of 135°.
(vi) Now, draw \(\overrightarrow{\mathrm{OE}}\) as the bisector of ∠QOD. Thus, ∠QOE = ∠DOE = 67\(\frac{1}{2}\)°

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.5

Question 1.
Draw AB of length 7.3 cm and find its axis of symmetry.
Solution:
Axis of symmetry of line segment \(\overline{\mathrm{AB}}\) will be the perpendicular bisector of \(\overline{\mathrm{AB}}\). So, draw the perpendicular bisector of \(\overline{\mathrm{AB}}\).
(i) Draw a line segment \(\overline{\mathrm{AB}}\) = 7.3 cm.
(ii) With A and B as centres and radius more than half of \(\overline{\mathrm{AB}}\), draw two arcs which intersect each other at C and D.
(iii) Join CD. Then CD is the axis of symmetry of the line segment \(\overline{\mathrm{AB}}\).

Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution:
(i) Draw a line segment \(\overline{\mathrm{AB}}\) = 9.5 cm.
(ii) With A and B as centres and radius more than half of \(\overline{\mathrm{AB}}\), draw two arcs which intersect each other at C and D.
(iii) Join CD. Then CD is the perpendi-cular bisector of \(\overline{\mathrm{AB}}\).

Question 3.
Draw the perpendicular bisector of \(\overline{\mathrm{XY}}\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether \(\overline{P X}=\) = \(\overline{P Y}\).
(b) If M is the mid-point of \(\overline{\mathrm{XY}}\). What can you say about the lengths of \(\overline{MX}\) and \(\overline{\mathrm{XY}}\).
Solution:
(i) Draw a line segment \(\overline{\mathrm{XY}}\) = 10.3 cm.
(ii) With X and Y as centres and radius more than half of \(\overline{\mathrm{XY}}\), draw two arcs which cut each other at C and D.
(iii) Join CD. Then, CD is the required perpendicular bisector of \(\overline{\mathrm{XY}}\).
(a) Take any point P on the bisector drawn.
With the help of divider we can check that \(\overline{P X}=\) = \(\overline{P Y}\).
(b) If M is the mid-point of \(\overline{\mathrm{XY}}\), then \(\overline{MX}\) = \(\frac{1}{2}\) \(\overline{\mathrm{XY}}\)

Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal points. Verify by actual measurement.
Solution:
(i) Draw a line segment AB = 12.8 cm.
(ii) Draw the perpendicular bisector of
\(\overline{\mathrm{AB}}\) which cuts it at C. Thus, C is the midpoint of \(\overline{\mathrm{AB}}\).
(iii) Draw the perpendicular bisector of \(\overline{\mathrm{AC}}\) which cuts it at D. Thus, D is the mid-point of \(\overline{\mathrm{AC}}\).
(iv) Again, draw the perpendicular bisector of \(\overline{\mathrm{CB}}\) which cuts it at E. Thus, E is the mid-point of \(\overline{\mathrm{CB}}\).

(v) Now, points D, C and E divide the line segment \(\overline{\mathrm{AB}}\) into four equal parts.
(vi) By actual measurement, we find that \(\overline{\mathrm{AD}}=\overline{\mathrm{DC}}=\overline{\mathrm{CE}}=\overline{\mathrm{EB}}=3.2 \mathrm{~cm}\)

Question 5.
With \(\overline{\mathrm{PQ}}\) of length 6.1 cm as diameter draw a circle.
Solution:
(i) Draw a line segment \(\overline{\mathrm{PQ}}\) =6.1 cm.
(ii) Draw the per¬pendicular bisector of PQ which cuts it at O. Thus, O is the mid-point of \(\overline{\mathrm{PQ}}\).
(iii) With 0 as centre and OP or OQ as radius, draws a circle where diameter is the line segment \(\overline{\mathrm{PQ}}\).

Question 6.
Draw a circle with centre C and radius 3.4 cm. Draw any chord \(\overline{\mathrm{AB}}\). Construct the perpendicular bisector of \(\overline{\mathrm{AB}}\) and examine if it passes through C.
Solution:
(i) Draw a circle Fig. with centre C and radius 3.4 cm.
(ii) Draw any chord \(\overline{\mathrm{AB}}\).
(iii) With A and B as centres and radius more than half of \(\overline{\mathrm{AB}}\), draw two arcs which cut each other at P and Q.
(iv) Join \(\overline{\mathrm{PQ}}\). Then, PQ is the perpendicular bisector of \(\overline{\mathrm{AB}}\).
(v) Clearly, this perpendicular bisector of \(\overline{\mathrm{AB}}\) passes through the centre C of the circle.

Question 7.
Repeat Question 6, if AB happens to be a diameter.
Solution:
(i) Draw a circle with centre C and radius 3.4 cm.
(ii) Draw its diameter \(\overline{\mathrm{AB}}\).
(iii) With A and B as centres and radius more than half of \(\overline{\mathrm{AB}}\), draw two arcs which cut each other at P arid Q.
(iv) Join \(\overline{\mathrm{PQ}}\). Then PQ is the perpendi¬cular bisector of \(\overline{\mathrm{AB}}\).
(v) Clearly, this perpendicular bisector of \(\overline{\mathrm{AB}}\) passes through the centre C of the circle.

Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the per-pendicular bisectors of these chords. Where do they meet ?
Solution:
(i) Draw a circle with centre 0 and radius 4 cm.
(ii) Draw any two chords \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) of this circle.
(iii) With A and B as centres and radius more that half of \(\overline{\mathrm{AB}}\), draw two arcs which cut each other at E and F.
(iv) Join EF. Thus, EF is the perpendi-cular bisector of chord \(\overline{\mathrm{AB}}\).
(v) Similarly, draw GH the perpendicular bisector of chord \(\overline{\mathrm{CD}}\) .
(vi) These two perpendicular bisectors meet at 0, the centre of the circle.

Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw
the perpendicular bisector of \(\overrightarrow{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\). Let them meet at P. Is \(\overline{\mathrm{PA}}=\overline{\mathrm{PB}}\) ?
Solution:
(i) Draw any angle with vertex 0.
(ii) Take a point A on one of its arms and B on another such that \(\overline{\mathrm{OA}}=\overline{\mathrm{OB}}\).
(iii) Draw perpen¬dicular bisectors of \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\).
(iv) Let them meet at P. Join PA and PB.
(v) With the help of divider we can check that \(\overline{\mathrm{PA}}=\overline{\mathrm{PB}}\).

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.4

Question 1.
Draw any line \(\overleftrightarrow{\mathrm{AB}}\) . Make any point M on it. Through M draw a
perpendicular to \(\overleftrightarrow{\mathrm{AB}}\) . (Use Ruler and compasses).
Solution:
(i.) With M as centre and a convenient radius, draw an arc intersecting the line \(\overleftrightarrow{\mathrm{AB}}\) at two points C and D.

(ii) With C and D as centres and a radius greater than MC, draw two arcs, which cut each other at P.
(iii) Join PM. Then PM is perpendicular to AB through the point M [Fig.].

Question 2.
Draw any line \(\overleftrightarrow{\mathrm{PQ}}\) . Take any point R not on it. Through R draw a perpendicular to \(\overleftrightarrow{\mathrm{PQ}}\) (Use Ruler and set-square).
Soution:
(i) Place a set-square on \(\overleftrightarrow{\mathrm{PQ}}\) such that one arm of its right-angle aligns along \(\overleftrightarrow{\mathrm{PQ}}\) .
(ii) Place a ruler along the edge opposite to the right-angle of the set- P square.

(iii) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set-square.
(iv) Join RM along the edge through R meeting \(\overleftrightarrow{\mathrm{PQ}}\) at M. Then, RM ⊥ PQ.

Question 3.
Draw a line T and a point X on it. Through X, draw a line \(\overleftrightarrow{\mathrm{XY}}\) perpendi¬cular to Z. Now, draw a perpendicular to \(\overleftrightarrow{\mathrm{XY}}\) at Y. (Use ruler and compasses).
Solution:
(i) Draw a line ‘l’ and take point X on it.
(ii) With X as centre and a convenient radius, draw an arc intersecting the line ‘l’ at two points A and B.
(iii) With A and B as centres and a radius greater than XA, draw two arcs, which cut each other at C.
(iv) Join XC and produce it to Y. Then XY is perpendicular to l.

(v) With D as centre and a convenient radius, draw an arc intersecting XY at two points C and D.
(vi) With C and D as centres and a radius greater than YD, draw two arcs, which cut each other at F.
(vii) Join YF, then YF is perpendicular to XY at Y.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.3

Question 1.
Draw any line segment \(\overline{\mathrm{PQ}}\). Without measuring \(\overline{\mathrm{PQ}}\) construct a copy of \(\overline{\mathrm{PQ}}\).
Solution:
(i) Given \(\overline{\mathrm{PQ}}\) whose length is not known.

(ii) Fix the compasses pointer on P and the pencil end on Q. The opening of the instru-ment now gives the length of \(\overline{\mathrm{PQ}}\).
(iii) Draw any line ‘l’. Choose a point A on ‘l’. Without changing the compasses setting, place the pointer on A.
(iv) Strike an arc that cuts ‘l’ at a point, say, B. Now \(\overline{\mathrm{AB}}\) is a copy of \(\overline{\mathrm{PQ}}\).

Question 2.
Given some line segment \(\overline{\mathrm{AB}}\), whose length you do not know, construct \(\overline{\mathrm{PQ}}\) such that the length of \(\overline{\mathrm{PQ}}\) is twice that of \(\overline{\mathrm{AB}}\).
Solution:
(i) Given \(\overline{\mathrm{AB}}\) whose length is not known.

(ii) Fix the compasses pointer on A and the pencils end on B. The opening instru¬ment now gives the length of \(\overline{\mathrm{AB}}\).
(iii) Draw any line ‘l’. Choose a point P on ‘l’. Without changing the compasses setting, place the pointer on P.
(iv) Strike an arc that cuts ‘l’ at a point R.
(v) Now, place the pointer on R and without changing the compasses setting, strike another arc that cuts ‘l’ at a point Q,
(vi) Thus, \(\overline{\mathrm{PQ}}\) is the required line segment whose length is twice that of AB.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.2

Question 1.
Draw a line segment of length 7.3 cm, using a ruler.
Solution:
Step 1. Place the zero mark of the ruler at a point A.
Step 2. Mark a point B at a distance of 7.3 cm from A and join AB.
Step 3. \(\overline{\mathbf{A B}}\) is the required line-segment of length 7.3 cm.

Question 2.
Construct a line segment of length 5.6 cm using ruler and compasses.
Solution:
(i) Draw a line’7’. Mark a point a on this line.
(ii) Place the compasses pointer on zero mark of the ruler. Open it to place the pencil point upto the 5.6 cm mark.

(iii) Without changing the opening of the compasses, place the pointer on A and swing an arc to cut 7’ at B.
(iv) \(\overline{\mathbf{A B}}\) is a line segment of the required length.

Question 3.
Construct \(\overline{\mathbf{A B}}\) of length 7.8 cm. From this cut off \(\overline{\mathbf{A C}}\) of length 4.7 cm. Measure \(\overline{\mathbf{B C}}\) .
Solution:

(i) Place the zero mark of the ruler at A.
(ii) Mark a point B at a distance 7.8 cm from A.
(iii) Again, mark a point C at a distnae 4,7 cm from A.
(iv) By measuring \(\overline{\mathbf{B C}}\) , we find that BC = 3.1 cm = (7.8 – 4.7) cm.

Question 4.
Given AB of length 3.9 cm, construct \(\overline{\mathbf{PQ}}\) such that the length of PQ is twice that of \(\overline{\mathbf{A B}}\) . Verify by measurement.
Solution:

(i) Draw a line ‘l’.
(ii) Construct \(\overline{\mathbf{PX}}\) such that length of \(\overline{\mathbf{PX}}\) = length of \(\overline{\mathbf{A B}}\) .
(iii) Then cut of \(\overline{\mathbf{XQ}}\) such that \(\overline{\mathbf{XQ}}\) also has the length of \(\overline{\mathbf{A B}}\) .
(iv) Thus, the length of \(\overline{\mathbf{PX}}\) and the length of \(\overline{\mathbf{XQ}}\) added together make twice the length of \(\overline{\mathbf{A B}}\) .
(v) Verification : By measurement we find that
PQ = 7.8 cm = 3.9 cm + 3.9 cm
= \(\overline{\mathbf{A B}}\) + \(\overline{\mathbf{A B}}\) = 2 x \(\overline{\mathbf{A B}}\) .

Question 5.
Given \(\overline{\mathbf{A B}}\) of length 7.3 cm and
\(\overline{\mathbf{C D}}\) of length 3.4 cm, construct a line
segment \(\overline{\mathbf{X Y}}\) such that the length of
\(\overline{\mathbf{X Y}}\) = the difference between the lengths
of \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{C D}}\) . Verify by measurement.
Solution:

(i) Draw a line 7’ and take a point X on it.
(ii) Construct \(\overline{\mathbf{XZ}}\) such that length of \(\overline{\mathbf{XZ}}\) = length of \(\overline{\mathbf{A B}}\) = 7.3 cm.
(iii) Then cut off \(\overline{\mathbf{ZY}}\) = length of \(\overline{\mathbf{CD}}\) = 3.4 cm.
(iv) Thus, the length of \(\overline{\mathbf{XY}}\) = length of \(\overline{\mathbf{A B}}\) – length of \(\overline{\mathbf{CD}}\) .
(v) Verification : By measurement, we find that length of \(\overline{\mathbf{XY}}\) = 3.9 cm = 7.3 – 3.4 cm = \(\overline{\mathbf{A B}}\) – \(\overline{\mathbf{CD}}\) .

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise

14.1

Question 1.
Draw a circle of radius 3.2 cm.
Solution:
Steps of construction :
(i) Open the compasses for the required radius 3.2 cm.
(ii) Mark a point ‘0’ with a sharp pencil where we want the centre of the circle to be.
(iii) Place the pointer of the compasses on 0.
(iv) Turn the compasses slowly to draw the circle.

Question 2.
With the same circle O, draw two circles of radii 4 cm and 2.5 cm.
Solution:
Steps of construction :
(i) Mark a point ‘O’ with a sharp pencil where we want the centre of the circle.
(ii) Open the compasses 4 cm.

(iii) Place the pointer of the compasses on O.
(iv) Turn the compasses slowly to draw the circle.
(v) Again open the compasses 2.5 cm
and place the pointer of the compasses at O. Turn the compasses slowly to draw the second circle.

Question 3.
Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained ? What figure is obtained if the diameters are perpendicular to each other ? How do you check you answer ?
Solution:
(i) By joining the ends of two diameters, we get a rectangle. By measuring, we find
AB = CD = 3 cm,
BC = AD = 2 cm

i.e., pair of opposite sides are equal.
∠A = ∠B = ∠C = ∠D = 90°
i.e., each angle is equal to 90°. Hence, ABCD is a rectangle, [see Fig.]

(ii) If the diameters are perpendicular to each other, then by joining the ends of two diameters, we get a square.

By measuring, we find that
AB = BC = CD = AD = 2.5 cm
i.e., four sides are equal.
∠A = ∠B = ∠C = ∠D = 90°
i.e., each angle is a right-angle. Hence, ABCD is a square [Fig.]

Question 4.
Draw any circle and mark points A, B and C such that:
(a) A is on the circle.
(b) B is in the interior o the circle.
(c) C is in the exterior of the circle.
Solution:
(i) Mark a point‘O’with sharp pencil where we want centre of the circle.
(ii) Place the poin-ter of the compasses at ‘O’, then move the compasses slowly to draw a circle. In Fig.
(a) Point A is on the circle.
(b) Point B 1 is in the interior of the circle.
(c) Point C is in the exterior of the circle.

Question 5.
Let A, B be the centres of two circles of equal radii, draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{CD}}\) are at right angles.
Solution:
Draw two circles of equal radii taking A and B as their centres such that each one.
of them passes through the centre of the other. Let them intersect at C and D. Join AB and CD. [Fig.]
Yes. \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{CD}}\) are at right angles, because ∠BOC = 90°.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 13 Symmetry Intext Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 13 Symmetry Intext Questions

TRY THIS (Page 346) :

Question.
You have two set squares in your ‘mathematical instrument box’. Are they symmetric ?
Solution:

The two set squares are not symmetrical.

TRY THIS (Page 348):

Form as many shapes as you can by combining two or more set squares. Draw them on squared paper and note their lines of symmetry.
Solution:
Lines l₁ l₂, l₃ l₄, and l₅ are the lines of symmetry respectively in Fig. (i), (ii), (iii), (iv) and (v).

TRY THESE (Page 356):

Question.
If you are 100 cm in front of a mirror, where does your image appear to be ? If you move towards the mirror, how does your image move ?
Solution:
Your image will appear at 100 cm behind the mirror.
(∵ Image is as far behind the mirror as the object is in front of it). If you move towards the mirror, it will move nearer and nearer.