Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 Practical Geometry Ex 14.2 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 14 Practical Geometry Exercise
14.2
Question 1.
Draw a line segment of length 7.3 cm, using a ruler.
Solution:
Step 1. Place the zero mark of the ruler at a point A.
Step 2. Mark a point B at a distance of 7.3 cm from A and join AB.
Step 3. \(\overline{\mathbf{A B}}\) is the required line-segment of length 7.3 cm.
![]()
![]()
Question 2.
Construct a line segment of length 5.6 cm using ruler and compasses.
Solution:
(i) Draw a line’7’. Mark a point a on this line.
(ii) Place the compasses pointer on zero mark of the ruler. Open it to place the pencil point upto the 5.6 cm mark.
![]()
(iii) Without changing the opening of the compasses, place the pointer on A and swing an arc to cut 7’ at B.
(iv) \(\overline{\mathbf{A B}}\) is a line segment of the required length.
Question 3.
Construct \(\overline{\mathbf{A B}}\) of length 7.8 cm. From this cut off \(\overline{\mathbf{A C}}\) of length 4.7 cm. Measure \(\overline{\mathbf{B C}}\) .
Solution:
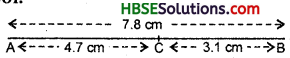
(i) Place the zero mark of the ruler at A.
(ii) Mark a point B at a distance 7.8 cm from A.
(iii) Again, mark a point C at a distnae 4,7 cm from A.
(iv) By measuring \(\overline{\mathbf{B C}}\) , we find that BC = 3.1 cm = (7.8 – 4.7) cm.
![]()
Question 4.
Given AB of length 3.9 cm, construct \(\overline{\mathbf{PQ}}\) such that the length of PQ is twice that of \(\overline{\mathbf{A B}}\) . Verify by measurement.
Solution:

(i) Draw a line ‘l’.
(ii) Construct \(\overline{\mathbf{PX}}\) such that length of \(\overline{\mathbf{PX}}\) = length of \(\overline{\mathbf{A B}}\) .
(iii) Then cut of \(\overline{\mathbf{XQ}}\) such that \(\overline{\mathbf{XQ}}\) also has the length of \(\overline{\mathbf{A B}}\) .
(iv) Thus, the length of \(\overline{\mathbf{PX}}\) and the length of \(\overline{\mathbf{XQ}}\) added together make twice the length of \(\overline{\mathbf{A B}}\) .
(v) Verification : By measurement we find that
PQ = 7.8 cm = 3.9 cm + 3.9 cm
= \(\overline{\mathbf{A B}}\) + \(\overline{\mathbf{A B}}\) = 2 x \(\overline{\mathbf{A B}}\) .
Question 5.
Given \(\overline{\mathbf{A B}}\) of length 7.3 cm and
\(\overline{\mathbf{C D}}\) of length 3.4 cm, construct a line
segment \(\overline{\mathbf{X Y}}\) such that the length of
\(\overline{\mathbf{X Y}}\) = the difference between the lengths
of \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{C D}}\) . Verify by measurement.
Solution:
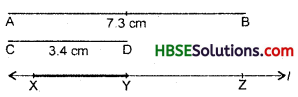
(i) Draw a line 7’ and take a point X on it.
(ii) Construct \(\overline{\mathbf{XZ}}\) such that length of \(\overline{\mathbf{XZ}}\) = length of \(\overline{\mathbf{A B}}\) = 7.3 cm.
(iii) Then cut off \(\overline{\mathbf{ZY}}\) = length of \(\overline{\mathbf{CD}}\) = 3.4 cm.
(iv) Thus, the length of \(\overline{\mathbf{XY}}\) = length of \(\overline{\mathbf{A B}}\) – length of \(\overline{\mathbf{CD}}\) .
(v) Verification : By measurement, we find that length of \(\overline{\mathbf{XY}}\) = 3.9 cm = 7.3 – 3.4 cm = \(\overline{\mathbf{A B}}\) – \(\overline{\mathbf{CD}}\) .