Author name: Bhagya

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 Square and Square Roots Ex 6.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 Square and Square Roots Exercise 6.3

Question 1.
What could be the possible ‘one’s’ digits of the square root of each of the following numbers ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i) 9801² = 9801 × 9801
Possible one’s digits =1 [∵ 1 × 1 = 1]

(ii) 99856² = 99856 × 99856
Possible one’s digits =6 [∵ 6 × 6 = 36]

(iii) 998001² = 998001 × 998001
∴ Possible one’s digits = 1

(iv) 657666025² = 657666025 × 657666025
∴ Possible one’s placed digit = 5 [∵ 5 × 5 = 25]

Question 2.
Without doing any calculation, fin#the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
(iv) 441
Solution:
(i) 153, (ii) 257 and (iii) 408 are surely not perfect squares.
[∵ The numbers end with 2, 3, 7, or 8 can never be a perfect square.]

Question 3.
Find the square roots of 100 and 169 by the method of repeated subtraction.
Solution:
For \(\sqrt {100}\)
(i) 100 – 1 = 99
(ii) 99 – 3 = 96
(iii) 96 – 5 = 91
(iv) 91 – 7 = 84
(v) 84 – 9 = 75
(vi) 75 – 11 = 64
(vii) 64 – 13 = 51
(viii) 51 – 15 = 36
(ix) 36 – 17 = 19
(x) 19 – 19 = 0

For \(\sqrt {169}\)
(i) 169 – 1 = 168
(ii) 168 – 3 = 165
……………………….
………………………..
……………………….
………………………..
……………………….
……………………….
………………………
(xiii) 23 – 23 = 0
From 100 and 169 we have subtracted successive odd numbers starting from 1 and obtain 0 at 10th and 13th step.
∴ \(\sqrt {100}\) = 10
and \(\sqrt {169}\) = 13

Question 4.
Find the square roots of the follow¬ing numbers by the Prime Factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100.
Solution:

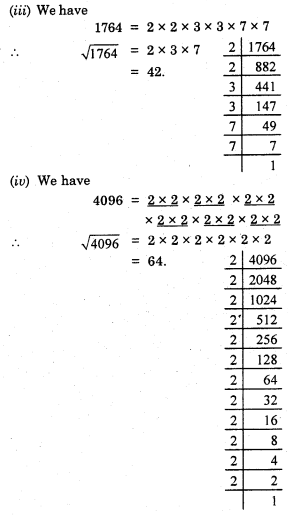
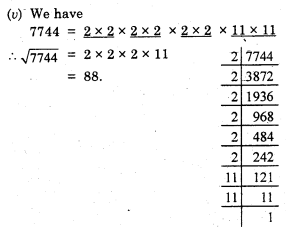
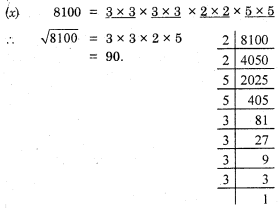
Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution:
By prime factorisation, we get
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

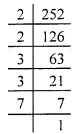
We see that in prime factorisation of 252, there exists a number 7 which is unpaired.
Hence, we will have to multiply 252 by 7 to make a pair of 7.
∴ 252 × 7 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{7 \times 7}\)
\(\sqrt {1764}\) = 2 × 3 × 7
= 42.

(ii) By prime factorisation, we get
180 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5

The number 5 is unpaired.
∴ The smallest number by which 180 should be multiplied to make it a perfect square is 5.
Now,
180 × 5 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
∴ 900 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
∴ \(\sqrt {900}\) = 2 × 3 × 5 = 30.

(iii) 1008 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7.
Here, 7 is unpaired
∴ We should multiply 1008 by to make it a perfect square.

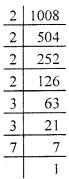
Now,
1008 × 7 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{7 \times 7}\)
⇒ 1056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
or \(\sqrt {1056}\) = 2 × 2 × 3 × 7
= 84.

(iv) 2028 = \(\underline{2 \times 2}\) × 3 × \(\underline{13 \times 13}\)
We see that the number 3 is unpaired.

∴ We should multiply 2028 by 3 to make it a perfect square.
Now,
2028 × 3 =\(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{13 \times 13}\)
Thus, 2084 = 2 × 2 × 3 × 3 × 13 × 3
∴ \(\sqrt {2084}\) = 2 × 3 × 13 = 78

(v) 1458 = 2 × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\).

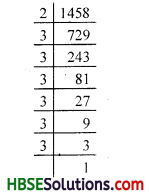
Since a number 2 is unpaired.
So, smallest number by which 1458 should be multiplied is 2.
∴ Required number
= 1458 × 2
= 2916
Thus,
2916 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\)
\(\sqrt {2916}\) = 2 × 3 × 3 × 3 = 54

(vi) By prime factorisation, we get
768 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)

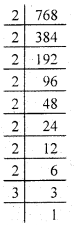
Since a number 3 is unpaired.
∴ We should multiply 768 by 3 to make it a perfect square .
Now,
768 × 3 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)
⇒ \(\sqrt {2304}\) = 2 × 2 × 2 × 2 × 3 = 48.

Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution:
(i) We have,
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7 (by prime factorisation)

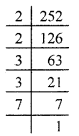
If we divide 252 by 7 then
252 ÷ 7 = 36 = 2 × 2 × 3 × 3
which is a perfect square.
Thus, the required smallest number is 7
and \(\sqrt {36}\) = 2 × 3 = 6

(ii) We have
2925 = \(\underline{5 \times 5}\) × \(\underline{3 \times 3}\) × 13

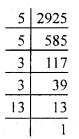
Since a number 13 is unpaired.
We should multiply 768 by 3 to make it a perfect square .
∴ 2925 ÷ 13 = 225
= \(\underline{5 \times 5}\) × \(\underline{3 \times 3}\)
which is a perfect square.
∴ The required smallest number is 13.
And \(\sqrt {225}\) = \(\sqrt{5 \times 5 \times 3 \times 3}\)
= 5 × 3 = 15

(iii) By prime factorisation, we get
396 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 11

If we divide 396 by 11, then
396 ÷ 11 = 36 = 2 × 2 × 3 × 3
which is a perfect square.
∴ The required smallest number is 11.
And, \(\sqrt {36}\) = 2 × 3 = 6

(iv) 2645 = 5 × \(\underline{23 \times 23}\)

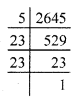
Since a number 5 is a unpaired.
So, we should divide 2645 by 5.
2645 ÷ 5 = 529 = 23 × 23
which is a perfect square.
∴ The required smallest number = 5
and \(\sqrt {529}\) = 23.

(v) By prime factorisation, we get
2800 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\) × 7

If we divide 2800 by 7, then
2800 ÷ 7 = 400
= \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\)
which is a perfect square.
Therefore, the required smallest number 7.
And, \(\sqrt {400}\) = 2 × 2 × 5 = 20

(vi) By prime factorisation, we get
1620 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × 5

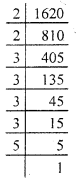
Since a number 5 is unpaired.
∴ We should divide 1620 by 5.
1620 ÷ 5 = 324
= \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\)
which is a perfect square.
Thus, \(\sqrt {324}\) = 2 × 3 × 3 = 18.

Question 7.
The students of Class VIII of a school donated Rs. 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students-in the class. Find the number of students in the class.
Solution:
Let the number of students in the class VIII be x.
Then, the rupees donated by each students will be Rs. x.
According to the given condition of the question :

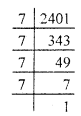
x × x = 2401
⇒ x² = 2401
⇒ x = \(\sqrt{2401}\)
= \(\sqrt{7 \times 7 \times 7 \times 7}\)
= 7 × 7
Hence, the number of students in the class is 49.

Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Let the no. of plants contains in each row be x.
Then, the no. of rows will be also x.
∴ According to the given condition of the question

Thus, x × x = 2025
⇒ x² = 2025
⇒ x² = 5² × 3² × 3²
⇒ x² = (5 × 3 × 3)²
⇒ x² = 452
x = 45.
∴ The number of rows and the number of plants in each row is 45.

Question 9.
Find the smallest square number that is divisible by each of the number 4, 9 and 10.
Solution:
This has to be done in three steps.

Step 1. First of all find the LCM of the numbers 4,9 and 10.
LCM of 4, 9 and 10 = 180
Step 2. Then, find the prime factorisation of the LCM so obtained i.e., 180.
180 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5
Step 3. Now, multiply the number 180 by 5 to make it a perfect square.

⇒ 180 × 5 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
⇒ 900 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
Now, 900 is obviously a perfect square.
So, the required square number is 900.

Question 10.
Find the smallest square number that is divisible by each of the number 8, 15 and 20.
Solution:
Follow the same procedure as explained in the solution of Question (9)
LCM of 8, 15 and 20 = 120

Prime factorisation of 120 = \(\underline{2 \times 2}\) × 2 × 3 × 5
We see that 2, 3 and 5 are not in pair.

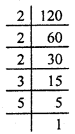
Therefore, 120 should be multiplied by 2 × 3 × 5 i.e., 30 in order to get a perfect square.
Hence, the required square number is
120 × 30 = 3600.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 Square and Square Roots Ex 6.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 Square and Square Roots Exercise 6.2

Question 1.
Find the square of the following numbers :
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46.
Solution:
(i) 32² = (30 + 2)²
= (30 + 2) (30 + 2)
= 30(30 + 2) + 2(30 + 2)
= 900 + 60 + 60 + 4 = 1024.

(ii) 35² = (3 × 4) hundreds + 25
= 12 × 100 + 25 = 1225

(iii) 86² = (80 + 6)²
= (80+ 6) (80+ 6)
= 80(80 + 6) + 6(80 + 6)
= 6400 + 480 + 480 + 36
= 7396

(iv) 93² = (90 + 3)²
= (90 + 3) (90 + 3)
= (90)² + 90 × 3 + 3 × 90 + (3)²
= 8100 + 270 + 270 + 9
= 8649

(v) 71² = (70 + 1)²
= (70)² + 2 × 70 × 1 + (1)²
[Using (a + b)² = a² + 2ab + b²]
= 4900 + 140 + 1 = 5041

(vi) 46² = (40 + 6)²
= (40)² + 2 × 40 × 6 + (6)²
= 1600 + 480 + 36 = 2116.

Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18.
Solution:
We have Pythagorean triplet (2m, m² – 1, m² + 1); where m > 1 (natural number).
Let us try one by one. .
Now, we take . .
m² – 1 = 6 ⇒ m² = 6 + 1 = 7
⇒ m = \(\sqrt {7}\) (not an integer)
m² + 1 = 6 ⇒ m² = 5
⇒ m = \(\sqrt {5}\) (not an integer)
2m = 6
⇒ m = \(\frac{6}{2}\) = 3 (is an integer)
Thus, m² – 1 = 3² – 1 = 9 – 1 = 8
and m² + 1 = 3² + 1 = 9 + 1 = 10
Therefore, the required triplet is (6, 8, 10).

(ii) m² – 1 = 14
or m² = 15
Then the value of m will not be an integer So, we try to take
m² + 1 = 14
or m² = 14 – 1 = 13
or m = \(\sqrt {13}\)
which is also not an integer.
So, take 2m = 14
⇒ m = 7.
Thus, m² – 1 = 7² – 1 = 49 – 1 = 48
and m² + 1 = 7² + 1 = 49 + 1 = 50
∴ The required triplet is (14, 48, 50).

(iii) Let m² – 1 = 16
⇒ m² = 17
or m = \(\sqrt {17}\)
which is not an integer
m² + 1 = 16
⇒ m² = 15
⇒ m = \(\sqrt {15}\) (not an integer)
and 2m = 16
⇒ m = 8.
Here, the value of m is an integer.
∴ m² – 1 = 8² – 1 = 64 – 1 = 63
and m²+ 1 = 8² + 1 = 64 + 1 = 65
Therefore, the required triplet is (16, 63, 65)

(iv) Let m² – 1 = 18
⇒ m² = 19
or m = \(\sqrt {19}\)
which is not an integer
Now, take m² + 1 = 18
⇒ m² = 17
or m = \(\sqrt {17}\)
which is also not an integer
So, let us take 2m = 18
⇒ m = 9 which is an integer.
∴ The required triplet is (18, 9² – 1, 9² + 1)
i.e., (18, 80, 81)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 Square and Square Roots Ex 6.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 Square and Square Roots Exercise 6.1

Question 1.
What will be the unit digit of the squares of the following numbers ?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555.
Solution:
(i) The unit digit of 81² = 1 [∵ 1² = 1]
(ii) The unit digit of 272² = 4 [∵ 2² = 4]
(iii) The unit digit of 799² = 1 [∵ 9² = 81]
(iv) The unit digit of 3853² = 9 [∵ 3² = 9]
(v) The unit digit of 1234² = 6 [∵ 4² = 16]
(vi) The unit digit of 26387² = 9 [∵ 7² = 49]
(vii) The unit digit of 52698² = 4 [∵ 8² = 64]
(viii) The unit digit of 99880² = 0 [∵ 0² = 0]
(ix) The unit digit of 12796² = 6 [∵ 6² = 36]
(x) The unit digit of 55555² = 5 [∵ 5² = 25]

Question 2.
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050.
Solution:
(i) 1057 is not a perfect square.
[∵ Perfect square never end with 2, 3, 7 or 8 at unit’s place]
(ii) 23453 is not a perfect square because the number end with 3.
(iii) Since 7928 end with 8. So, it is not a perfect square.
(iv) Since 222222 end with 2. So, it is not a perfect square.
(v) 64000 because it do not have even number of zeros at the end.
(vi) 89722 is not a perfect square.
[∵ Perfect square never end with 2, 3, 7 or 8]
(vii) 222000 is not a perfect square as the number of zeros in the end is 3 (odd number).
(viii) 505050 is not a perfect square because number of zeros in the ends is 1 (odd number).

Question 3.
The squares of which of the following would be odd numbers ?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004.
Solution:
(i) 431 and (ii) 7779.
Because squares of odd number are always
odd.

Question 4.
Observe the following pattern and find the missing digits.
11² = 121
101² = 10201
1001² = 1002001
100001² = 1………….. 2 …………….. 1
10000001² = ………………..
Solution:
100001² = 10000200001
and 10000001² = 100000020000001
[Using pattern given in the question]

Question 5.
Observe the following pattern and supply the missing numbers.
11² = 121
101² = 10201
10101² = 102030201
1010101² = ………………..
………………..² = 10203040504030201
Solution:
1010101² = 1020304030201
and 101010101² = 10203040504030201
[Using pattern given in the question]

Question 6.
Using the given pattern, find the missing numbers.
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + _² = 21²
5² + _² + 30² = 31²
6² + 7² + _² = _²
To find pattern : Third number is related to first and second number. How ?
Fourth number is related to third number. How ?
Solution:
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
and 6² + 7² + 42² = 43²
∵ 1 × 2 = 2, 2 + 1 = 3
2 × 3 = 6, 6 + 1 = 7
3 × 4 = 12, 12 + 1 = 13
…………………………….
and so on.

Question 7.
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23.
Solution:
(i) 1 + 3 + 5 + 7 + 9
[Sum of first five odd numbers]
= 5² = 25.

(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 [Sum of first ten odd numbers]
= 10² = 100.

(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
= 12² = 144.
[Sum of first twelve odd numbers]

Question 8.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of ii odd numbers.
Solution:
(i) 49 = (7)²
= Sum of first 7 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13

(ii) Similarly,
121 = (11)²
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21

Question 9.
How many numbers lie between squares of the following numbers ?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution:
(i) Here, n = 12 and n + 1 = 13
∴ 2n numbers non perfect square numbers lie between square of n2 and (n + 1)²
Thus, 2 × 12 = 24
such numbers lie between 12² and 13².

(ii) Similarly,
2 × 25 = 50
numbers lie between 25² and 26².
2 × 99 = 198

and (iii) 2 × 99 = 198
numbers lie between 99² and 100².

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 Square and Square Roots InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 Square and Square Roots InText Questions

Try These (Page 90)

Question 1.
Find the perfect square numbers between
(i) 30 and 40
(ii) 50 and 60.
Solution:
(i) The perfect square number between 30 and 40 is 36. [∵ 6² = 36]
(ii) There is no perfect square number between 50 and 60.

Try These (Page 90-91)

Question 1.
Can we say whether the following numbers are perfect squares ? How do we know ?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061
Write five numbers which you can decide by looking at their one’s digit that they are not square numbers.
Solution:
(i) 1057 can not be a perfect square because the digit in the one’s place is 7.
(ii) 23453 is not a perfect square.
[∵ The digit end with 3]
(iii) 7928 is not a perfect square.
[∵ The digit end with 8]
(iv) 222222 is not a perfect square.
[∵ The digit end with 2]
(v) 1069 may be a perfect square.
[For perfect square the digits in the one’s place must be 0, 1, 4, 5, 6 or 9]
(vi) 2061 may be a perfect square.

Question 2.
Write five numbers which you cannot decide just by looking at their unit’s digit (or one’s place) whether they are square numbers or not.
Solution:
Five numbers which is not a perfect square are 223, 237, 25968, 7727 and 8888.

Try These (Page 91)

Question 1.
Which of 123², 77², 82², 161², 109² would end with digit 1 ?
Solution:
If a number has 1 or 9 in the unit’s place, the it’s square ends in 1.
∴ 161² = 161 × 161 and 109
= 109 × 109
are the two numbers whose unit’s place ends in 1 and 9 respectively.

Question 2.
Which of the following numbers would have digit 6 at unit place.
(ii) 19²
(ii) 24²
(iii) 26²
(iv) 36²
(v) 34²
Solution:
(ii) 24²
(iii) 26²
(iv) 36² and
(v) 34² would have digit 6 at unit place.
[∵ One’s place should be either 4 or 6]

Try These (Page 92)

Question 1.
What will be the “one’s digit” in the square of the following numbers ?
(i) 1234
(ii) 26387
(iii) 52698
(iv) 99880
(v) 21222
(vi) 9106.
Solution:
(i) 6 [∵ 4² = 16]
(ii) 9 [∵ 7² = 49]
(iii) 4 [∵ 8² = 64]
(iv) 0 [∵ 0² = 0]
(v) 4 [∵ 2² = 4]
(vi) 6 [∵ 6² = 6]

Question 2.
The square of which of the following numbers would be an odd number/an even number ? Why ?
(i) 727
(ii) 158
(iii) 269
(iv) 1980.
Solution:
(i) 727, odd number.
(ii) 158, even number.
(iii) 269, odd number.
(iv) 1980, even number.
[∵ Squares of even numbers are always even and squares of odd numbers are.always odd]

Question 3.
What will be the number of zeros in the square of the following numbers ?
(i) 60
(ii) 400.
Solution:
(i) Two zeros
(ii) Four zeros.

Try These (Page 94)

Question 1.
How many natural numbers lie between 9² and 10²? Between 11² and 12²?
Solution:
Total numbers of natural number between 9² and 10².
2n = 2 × 9 = 18
Here, n = 9
Similarly, total number of natural numbers between
11² and 12² = 2n
= 2 × 11 = 22.

Question 2.
How many non square numbers lie between the following pairs of numbers ?
(i) 100² and 101²
(ii) 90² and 91²
(iii) 1000² and 1001².
Solution:
(i) Non square numbers between 1002 and 1012
= 2n, where n smallest number.
= 2 × 100 = 200

(ii) Non square numbers between 90² and 91²
= 2n = 2 × 90= 180 [∵ = 90]

(iii) Non square numbers between 1000² and 1001²
= 2n = 2 × 1000 [∵ n = 1000]
= 2000.

Try These (Page 94)

Question 1.
Find whether each of the following numbers is a perfect square or not ?
(i) 121
(ii) 55
(iii) 81
(iv) 49
(v) 69.
Solution:
(i) 121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
……………………
……………………
and so on.
We will get the result is zero in the end after 11 steps.
So, 121 is a perfect square.
[Do the same calculations as explained in part (i)]
(ii) 55 is not a perfect square,
(iii) 81 is perfect square.
(iv) 49 is a perfect square.
(v) 69 is not a perfect square.

Try These (Page 95)

Question 1.
Express the following as the sum of two consecutive integers.
(i) 21²
(ii) 13²
(iii) 11²
(iv) 19²
Solution:
(i) 21² = 441
= [\(\frac{21^{2}-1}{2}\) + \(\frac{21^{2}+1}{2}\)]
= 220 + 221

(ii) 13² = 169
= [\(\frac{13^{2}-1}{2}\) + \(\frac{13^{2}+1}{2}\)]
[n² = \(\frac{n^{2}-1}{2}\) + \(\frac{n^{2}+1}{2}\)]
= \(\frac{169-1}{2}\) + \(\frac{169+1}{2}\) = 81 + 82

(iii) Similarly, 11² = 121 = 60 + 61.
192 = 361 = 180 + 181.

Question 2.
Do you think the reverse is also t rue, i.e., is the sum of any two consecutive positive integers is perfect square of a number ? Give example to support your answer.
Solution:
No, the reverse is not true
4 + 5 = 9 = 3²
but 6 + 7 = 13
is not a perfect square.

Try These (Page 95)

Question 1.
Write the square, making use of the above pattern.
(i) 111111²
(ii) 1111111²
Solution:
(i) 111111² = 12345654321
[∵ 1² = 1, 11² = 121, 111² = 12321 and so on]
(ii) 1111111² = 1234567654321
[Follow the same pattern]

Question 2.
Can you find the square of the following numbers using the above pattern ?
(i) 6666667²
(ii) 66666667².
Solution:
(i) 6666667² = 44444448888889
(ii) 66666667² = 4444444488888889
Observe the following pattern :
7² = 49
67² = 4489
667² = 444889
6667² = 44448889
………………………….
………………………….

Try These (Page 97)

Question 1.
Find the squares of the following numbers containing 5 in unit’s place.
(i) 15
(ii) 95
(iii) 105
(iv) 205.
Solution:
(i) 15² = (1 × 2) hundreds + 25,
= 2 × 100 + 25 = 225
(ii) 95² [∵ (a₅)² = a(a + 1) hundred + 25,
where (a₅) is a number with unit digit as 5]
= (9 × 10) hundreds + 25
= 9000 + 25 = 9025
(iii) (105)² = (10 × 11) × 100 + 25
= 11025
(iv) (205)² = (20 × 21) × 100 + 25
= 42025

Try These (Page 99)

Question 1.
(i) 11² = 121. What is the square root of 121 ?
(ii) 14² = 196. What is the square root of 196?
Solution:
(i) Since 11² = 121
∴ Square root of 121 = 11

(ii) Since 14² = 196
∴ Square root of 196 = 14.

Try These (Page 100)

Question 1.
By repeated subtraction of odd numbers starting from 1, find whether the following numbers are perfect squares or not ? If the number is a perfect square then
find its square root.
(i) 121
(ii) 55
(iii) 36
(iv) 49
(v) 90.
Solution:
(i) 121 – 1 = 120 120 – 3 = 117
117 – 5 = 112 112 – 7 = 105
105 – 9 = 96 96 – 11 = 85
85 – 13 = 72 72 – 15 = 57
57 – 17 = 40 40 – 19 = 21
21 – 21 = 0
We observe that the number 121 reduced to zero after subtracting 11 consecutive odd numbers starting from 1. Thus, 121 is a perfect square.
∴ 121 = 11² ⇒ \(\sqrt {121}\) = 11

(ii) 55 – 1 = 54 54 – 3 = 51
51 – 5 = 46 46 – 7 = 39
39 – 9 = 30 30 – 11 = 19
19 – 13 = 6
Here the no. do not reduced to zero. So, 55 is not a perfect square.

(iii) 36 – 1 = 35 35 – 3 = 32
32 – 5 = 27 27 – 7 = 20
20 – 9 = 11 11 – 11 = 0
We obtained 0 at 6th step
∴ 36 = 6² (It is a perfect square)
or \(\sqrt {36}\) = 6

(iv) 49 – 1 = 48 48 – 3 = 45
45 – 5 = 40 40 – 7 = 33
33 – 9 = 24 24 – 11 = 13
13 – 13 = 0
We have subtracted successive odd numbers starting from 1 and obtained 0 at 7th step.
∴ 49 = 7² ⇒ \(\sqrt {49}\) = 7 .
This is a perfect square.

(v) 90 – 1 = 89 89 – 3 = 86
86 – 5 = 81 81 – 7 = 74
74 – 9 = 65 65 – 11 = 54
54 – 13 = 41 41 – 17 = 24
24 – 19 = 5
∵ We do not obtain zero in the end.
∴ 90 is not a perfect square.

Try These (Page 105)

Question 1.
Without calculating square roots, find the number of digits in the square root of the following numbers :
(i) 25600
(ii) 100000000
(iii) 36864
Solution:
(i) 25600
Here, the number of digits (n) = 5 (odd)
∴ The number of digits in the square roots of 25600
= \(\frac{(n+1)}{2}\) = \(\frac{(5+1)}{2}\) = 3

(ii) 100000000
Here, the number of digits (n) = 9 (odd)
∴ The number of digits in the square roots of the number
= \(\frac{(n+1)}{2}\) = \(\frac{(9+1)}{2}\) = 5
∴ The number of digits in the square of the number
= \(\frac{(n+1)}{2}\) = \(\frac{(5+1)}{2}\) = \(\frac{(6)}{2}\) = 3

Try These (Page 107)

Question 1.
Estimate the value of the following to the nearest whole number :
(i) \(\sqrt {80}\)
(ii) \(\sqrt {1000}\)
(iii) \(\sqrt {350}\)
(iv) \(\sqrt {500}\)
Solution:
(i) We know that
80 < 81 < 100
and \(\sqrt {81}\) = 9 and \(\sqrt {100}\) = 10
But 9 < \(\sqrt {80}\) < 10
Now, \(\sqrt {80}\) is much closer to 9² = 81
then 10² = 100
So, \(\sqrt {80}\) is approximately 9.

(ii) We know that
100 < 1000 < 10000
and \(\sqrt {100}\) = 10
\(\sqrt {1000}\) = 100
So, 10 < \(\sqrt {1000}\) < 10
But still we are not very close to square number.
We know that 31² = 961
and 32² = 1024
But 1024 is much closer to 1000 than 961.
So, \(\sqrt {1000}\) = 32 (approximately).

(iii) We know that
100 < 350 < 400
and \(\sqrt {100}\) = 10
\(\sqrt {400}\) = 20
So, 10 < \(\sqrt {350}\) < 20
But still you are not very close to the square number.
We know that 18² = 324 and 19² = 361
∴ 18 < \(\sqrt {350}\) < 19
and 350 is much closer to 361 than to 324
So, \(\sqrt {350}\) is approximately equal to 19.

(iv) We know that
100 < 500 < 625
and < \(\sqrt {100}\) =10
< \(\sqrt {625}\) = 25
So, 10 < \(\sqrt {500}\) < 25
But we are still not very close to the square number.
We know that
22² = 484 and 23² = 529
∴ 2 < \(\sqrt {500}\) < 23
But 500 is closer to 484 than to 529.
Hence, < \(\sqrt {500}\) is approximately equal to 22.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 5 Data Handling InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 5 Data Handling InText Questions

Think, Discuss and Write (Page 71)

Question 1.
If we change the position of any of the bars of a bar graph, would it change the information being conveyed? Why?
Answer:
Yes, It would change the information being conveyed because bar represents information for particular year, subject etc. If you change or shift the position of bar it would convey different meaning.

Try These (Page 71)

Question 1.
Draw an appropriate graph to represent the given information :

Solution:
A Pictograph :

Question 2.

Solution:
Double bar graph

Question 3.
Percentage wins in ODI by 8 top cricket teams :

Solution:
Double bar graph :

Try These (Page 72)

Question 1.
A group of Students were asked to say which animal they would like most to have as a pet. The results are given below :
dog, cat, cat, fish, cat, rabbit, dog, cat, rabbit, dog, cat, dog, dog, dog, cat, cow, fish, rabbit, dog, cat, dog, cat, cat, dog, rabbit, cat, fish, dog.
Make a frequency distribution table for the same.
Solution:

Try These (Page 73)

Question 1.
Study the following frequency distribution table and answer the questions given below:
Frequency Distribution of Daily Income of 550 workers of a factory

(i) What is the size of the class intervals ?
(ii) Which class has the highest frequency ?
(iii) Which class has the lowest frequency ?
(iv) What is the upper limit of the class interval 250-275 ?
(v) Which two classes have the same frequency ?
Solution:
(i) Size of the class intervals = 25
(ii) 200—225.
(iii) 300—325
(iv) 275
(v) 150—175 and 225 250.

Question 2.
Construct a frequency distribution table for the data on weights (in kg) of 20 students of a class using intervals 30—35, 36—40 and so on.
40, 38, 33, 48, 60, 53, 31, 46, 34, 36, 49, 41, 55, 49, 65, 42, 44, 47, 38, 39.
Solution:

Try These (Page 75-76)

Question 1.
Observe the histogram (Fig. 5.3) and answer the questions given below :

(i) What information is being given by the histogram ?
(ii) Which group contains maximum girls ?
(iii) How many girls have a height of 145 cms and more ?
(iv) If we divide-ihe girls into the following three categories, how many would there be in each?
150 cm and more — Group A
140 cm to less than 150 cm—Group B
Less than 140 cm — Group C
Solution:
(i) Height (in cm) of number of girls of class VII.
(ii) (140 – 145) contains maximum girls.
(iii) No. of girls have height 145 cms and more = 4 + 2 + 1 = 7.
(iv) 150 cm and more —Group A —3 girls 140 cm to less than 150—Group B—11 girls Less than 140 cm—Group C —6 girls.

Try These (Page 78)

Question 1.
Each of the following pie charts (Fig. 5.7) gives you a different piece of information about your class. Find the fraction of the circle representing each of these Information.

Solution:
(i) (a) The proportion of sector for girls

(b) Love Hindi = \(\frac{15 \%}{100 \%}\) = \(\frac{3}{20}\)

Question 2.
Answer the following questions based on the pie chart given (Fig. 5.8).

(i) Which type of programmes are viewed the most ?
(ii) Which two types of programmes have number of viewers equal to those watching sports channels ?
Solution:
(i) Entertainment.
(ii) (News and Information Channels together have equal number of viewers to those watching sports channels.

Try These (Page 81)

Question 1.
Draw a pie chart of the data given below.
The time spent by a child during a day.
Sleep—8 hours
School—6 hours
Homework—4 hours
Play—4 hours
Others—2 hours
Solution:

Now, we make the pie chart as under :

Think, Discuss and Write (Page 81)

Which form of graph would be appropriate to display the following data ?
Question 1.
Production of food grains of a state.

Solution:
A bar graph or pie chart.

Question 2.
Choice of food for a group of people.

Solution:
A bar graph or pie chart.

Question 3.
The daily income of a group of a factory workers.

Solution:
A Histogram or a Bar Graph.

Try These (Page 83-84)

Question 1.
If you try to start a scooter, what are the possible outcomes ?
Answer:
Possible outcomes are either a scooter will start or do not start.

Question 2.
When a die is thrown, what are the six possible outcomes ?
Answer:
Six possible outcomesare 1, 2, 3, 4, 5 or 6.

Question 3.
When you spin the wheel shown, what are the possible out-comes ? (Fig. 5.15) List them.
(Outcome here means the sector at which the pointer stops).

Answer:
Possible outcomes are pointer will stop at A, B or C.

Question 4.
You have a bag with five identical balls of different colours and you are to puli out (draw) a ball without looking at it; list the outcomes you would get (Fig. 5.16).

Answer:
Possible outcomes are : Red ball, White ball, Blue ball, Green ball or Yellow ball.
So, five outcomes are possible,

Think, Discuss and Write (Page 84)

Question 1.
In throwing a die :
(i) Does the first player have a greater chance of getting a six ?
(ii) Would the player who played after him have a lesser chance of getting a six ?
(iii) Suppose the second player got a six. Does it mean that the third player would not have a chance of getting a six ?
Solution:
(i) No,
(ii) No and
(iii) No.
Reason : You cannot control the result.
Throwing a die is random experiment.

Try These (Page 86)

Question 1.
Suppose you spin the wheel:
(i) List the number of outcomes of getting a green sector and not getting a green sector on this wheel (Fig. 5.17).

(ii) Find, the probability of getting a green sector.
(iii) Find the probability of not getting a green sector.
Solution:
(i) Total number of outcomes = 8
Number of outcomes of getting a green sector = 5 (Green sectors).
Number of outcomes of do not getting a green sector = 3 (Red sectors).

(ii) Probability of getting a green sector = \(\frac{Number of outcomes that make the event}{Total number of outcomes of the experiment}\)
= \(\frac{5}{8}\)

(iii) Probability of not getting a green sector = \(\frac{5}{8}\)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 5 Data Handling Ex 5.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 5 Data Handling Exercise 5.3

Question 1.
List the outcomes you can see in these experiments.
(a) Spinning a wheel
(b) Tossing two coins together.

Solution:
(a) Outcomes you can see in Spinning a wheel are : A, B, C, D and A.
(b) Possible outcomes are : (HH), (HT). (TT) and(TH).

Question 2.
When a die is thrown, list outcomes of an event of getting
(i) (a) a prime number
(b) not a prime number
(ii) (a) a number greater than 5
(b) a number not greater than 5.
Solution:
(i) (a) A prime number : 2 3, 5.
(b) Not a prime number : 4, 6.
(ii) (a) a number greater that 5 is 6.
(b) a number not greater than 5 are : 1, 2, 3 and 4.

Question 3.
Find the :
(a) Probability of the pointer stopping on Din (Question 1-(a)).
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards ?
(c) Probability of getting a red apple. (See Fig. 5.19).

Solution:
(a) Number of possible outcomes for pointer stopping on D = 1.
Total number of outcomes of the experiment = 5.
∴ P(the pointer stopping on D) = \(\frac{1}{5}\)

(b) Total no. of aces = 4
Total number of outcomes = 52
∴ P (an ace) = \(\frac{4}{52}\) = \(\frac{1}{13}\)

(c) Number of Red apples = 4
Total number of outcomes (apples) = 7
∴ P (getting a red apple) = \(\frac{4}{7}\)

Question 4.
Numbers of 1 to 10 are written on ten separate slips (one number of one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of:
(i) getting a number 6 ?
(ii) getting a number less than 6 ?
(iii) getting a number greater than 6 ?
(iv) getting a 1-digit number ?
Solution:
(i) Number of slip written 6 on it = 1
Total number of outcomes (slips) = 10
∴ P (getting a number 6) = \(\frac{1}{10}\)

(ii) Numbers less than 6 are : 1, 2, 3, 4, 5 = 5
Total number of slips (outcomes) = 10
∴ P(getting a number less than 6) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

(iii) Numbers greater than 6 are : 7, 8, 9, 10 = 4
∴ P(getting a number greater than 6) = \(\frac{4}{10}\) = \(\frac{2}{5}\)

(iv) One digit numbers are : 1,2, 3, 4, 5, 6, 7, 8 and 9 = 9.
Total number of outcomes =10
∴ P(1-digit number) = \(\frac{9}{10}\)

Question 5.
If you have a spinning wheel, with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector ? What is the probability of getting a non blue sector ?
Solution:
Total number of outcomes (sectors) of the experiment = 3 + 1 + 1 = 5.
Number of green sector = 3
Number of non blue sector
= 3 green + 1 red 4
∴ P(getting a green sector) = \(\frac{3}{5}\)
P(getting a non blue sector) = \(\frac{4}{5}\)

Question 6.
Find the probabilities of the events given in Question 2.
Solution:
(i) (a) P(a prime number) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
(b) P(not a prime number) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(ii) (a) P(a number greater than 5) = \(\frac{1}{6}\)
(b) P(a number not greater than 5) = \(\frac{4}{6}\) = \(\frac{2}{3}\)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 5 Data Handling Ex 5.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 5 Data Handling Exercise 5.2

Question 1.
A survey was made to find the I type of music that a certain group of young people liked in a city. Adjoining pie chart shows the findings of this survey.
From this pie chart answer the following:
(i) If 20 people liked classical music, how many young people were surveyed ?

(ii) Which type of music is liked by the maximum number of people ?
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make ?
Solution:
(i) No. of people liked classical music = 20.
Percentage of people liked classical music = 10%.

This is in direct variation
\(\frac{20}{10}\) = \(\frac{x}{100}\)
⇒ 10x = 20 × 100
⇒ x = \(\frac{2000}{10}\) = 200 people.
Aliter : If 10% = 20 people 20
then 100% = \(\frac{20}{10 \%}\) × 100%
= 200 people.

(ii) Light music.
(iii)No. of semi classical CD’s
= 20% of 1000 = \(\frac{20}{100}\) × 1000 = 200
No. of classical music CD’s
= 10% of 1000 = \(\frac{10}{100}\) × 1000 = 100
No. of Folk music CD’s
= \(\frac{30}{100}\) × 1000 = 300
No. of light music CD’s 40
= \(\frac{40}{100}\) × 1000 = 400.

Question 2.
A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer.
(i) Which season got the most votes ?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.

Solution:
(i) Winter.
(ii) Central angle = \(\frac{Value of Item}{Total value}\) 360°
∴ Central angle for Summer season
= \(\frac{90}{360}\) × 360° = 90°
Central angle for Rainy season
= \(\frac{120}{360}\) × 360° = 120°
and Central angle for Winter season
= \(\frac{150}{360}\) × 360° = 150°

Question 3.
Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.

Find the proportion of each sector. For example, Blue is \(\frac{18}{360}\) = \(\frac{1}{2}\); Green is \(\frac{9}{36}\) = \(\frac{1}{4}\) and so on. Use this to find the corresponding angles.
Solution:

Now, we make the pie chart as-shown below musing protractor, compasses and ruler.

Question 4.
The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions :
(i) In which subject did the student score 105 marks ?
[Hint: For 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle ?]
(ii) How many more marks were obtained by the student in Mathematics than in Hindi ?
(iii) Examine whether the sum of the marks obtained m Social Science and Mathematics is more than that in Science and Hindi.
[Hint: Just study the central angles.]

Solution:
(i) For 540 marks, the central angle = 360°
So, for I mark, the central angle = \(\frac{360^{\circ}}{540}\)
So, for 105 marks, the central angle = \(\frac{360^{\circ}}{540}\) × 108 = 70°
∴ It is obvious, from the pie chart that the student scored 105 marks, in ‘Hindi’ as central angle for ‘Hindi’ is 70°.

(ii) ∵ For 360° marks obtained = 540
∴ For 1° mark obtained = \(\frac{540}{360^{\circ}}\)
For 90° marks obtained = \(\frac{540}{360^{\circ}}\) × 90°
∴ Marks obtained in Mathematics = 135
Marks obtained in Hindi = 105
Difference in marks = 135 – 105 = 30

(iii) Marks obtained in Social Science
= \(\frac{Total marks}{Total central angle}\) × central angle of an Item
= \(\frac{540}{360^{\circ}}\) × 65° = 97.5
Marks obtained in Science
= \(\frac{540}{360^{\circ}}\) × 80° = 120
Marks obtained in (SST + Math)
= 97.5 + 135 = 232.5
Marks obtained in (Science + Hindi)
= 120 + 105 = 225
Alternative method:
Sum of central angles in (SST + Math)
= 65° + 90° = 155°
Sum of central angles in (Science + Hindi)
= 80 + 70 = 150°
So, sum of the marks obtained in SST and Mathematics is more than that in Science and Hindi.

Question 5.
The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.

Solution:

Now, we make the pie chart as shown below

Haryana State Board HBSE 8th Class Maths Solutions Chapter 5 Data Handling Ex 5.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 5 Data Handling Exercise 5.1

Question 1.
For which of these would you use a histogram to show the data ?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passenger boarding trains from 7:00 am to 7:00 pm at a station.
Give reasons for each.
Solution:
(a) Different areas A, B, C has a certain number of letters. So, there is no class interval exist. Thus, it is better to represent the data by a bar graph than by a histogram.
(b) Height of competitors lies between a certain range. So, class interval exist.
Therefore, we use a histogram to represent the data.
(c) There is no class interval. There is a name of five companies. So, we cant show the data by a histogram.
(d) Class intervals like 7 am – 9 am, 9 am – 11 am etc. are necessary to show the number of passengers boarding to trains during that time intervals.
So, a histogram is suitable representation of data.

Question 2.
The shoppers who come to a departmental store are marked as : man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning :
WWWGBWWMGGMMWWWWG B MWB GGMWWMMWWWMWBWG MWWWWGWMMWWMWGWMGW M M B G G W.
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution:
Frequency Distribution Table :

Question 3.
The weekly wages (in Rs.) of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840.
Using tally marks make a frequency table with intervals as 800-810, 810-820 and so on.
Solution:

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions :
(i) Which group has the maximum number of workers ?
(ii) How many workers earn Rs. 850 and more ?
(iii) How many workers earn less than Rs. 850?
Solution:

(i) Group (830—840) has maximum number of workers.
(ii) No. of workers whose earning Rs. 850 and more = 1 + 3 + 1 + 1 + 4=10
(iii) No. of workers whose earning is less than 850 = 3 + 2 + 1 + 9 + 5 = 20.

Question 5.
The number of hours for which students of a particular class watched television during holidays is shown through the given graph.
Answer the following:
(i) For how many hours did the maximum number of students watch TV ?
(ii) How many students watched TV for less than 4 hours ?
(iii) How many students spent more than 5 hours in watching TV ?

Solution:
(i) Maximum number of students watched TV = (4 – 5) hours.
(ii) No. of students watched TV less than 4 hours = 4 + 8 + 32 = 44 hours.
(iii) Students spent more than 5 hours in watching TV = 8 + 6 = 14 hours.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.5 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 4 Practical Geometry Exercise 4.5

Question 1.
Draw the following :
1. The square READ with RE = 5.1 cm.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
3. A rectangle with adjacent sides of lengths 5 cm and 4 cm.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm.
Solution:
(1) Rough Sketch:

Steps of Construction:
(i) Draw RE = 5.1 cm.
(ii) Make ∠YRE = 90° and ∠REX = 90°
(iii) Cut off DR = AE = 5.1 cm.
(iv) Join DA.
(v) DEAR is a required square.

(2) Rough Sketch:

Theory : Diagonals of a rhombus bisect each other at 90°
i.e., OA = OC = \(\frac{6.4}{2}\) = 3.7 cm and OD = OB = \(\frac{5.2}{2}\) = 2.6 cm
∠AOB = 90°
Steps of Construction :
(i) Draw BD = 5.2 cm.
(ii) Draw perpendicular bisector XY of BD.
(iii) Cut off OA = OC = 3.7 cm on the opposite side of DB.

(iv) Join AB, AD, CD and BC.
(v) ABCD is a required rhomus.

(3) Rough Sketch :

Theory : A rectangle has equal opposite sides and each angles are 90°.
i.e. AB = DC = 5 cm DA = CB = 4 cm
∠A = ∠B = ∠C = ∠D = 90°
Steps of Construction :
(i) Draw a line segment AB = 5 cm.
(ii) Construct ∠A = ∠B = 90°.
(iii) Cut off AD = BC = 4 cm.
(iv) Join DC.
(v) You have a required rectangle ABCD.

4. Theory: Opposite sides of a parallelogram are equal and sum of a adjacent angle is 180°.

i.e. OK = YA = 4.2 c.m. and OY = KA = 4.2 cm.
Steps of Construction :
(i) Draw OK = 5.5 cm
(ii) Let ∠K = 80°, so construct ∠OKX = 80°
(iii) Cut of FKA = 4.2 cm in KX.
(iv) Let the point be A.

(v) Draw arcs of 5.5 cm and 4.2 cm with centre as A and O respectively.
Note : You may take one angle of any measurement.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 4 Practical Geometry Exercise 4.4

Question 1.
Construct the following quadrilaterals :
(i) Quadrilateral
DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
(ii) Quadrilateral
TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U = 120°
Solution:
Rough Sketch :

Steps of Construction :
(i) Draw EA = 5 cm.
(ii) Make ∠DEA = 60° and ∠EAR = 90°.

(iii) Cut off RA = 4.5 cm and DE = 4 cm.
(iv) Join DR.
(v) DEAR is the required quadrilateral.

(ii) Rough Sketch

Steps of Construction :
(i) Draw RU = 3 cm.
(ii) Construct ∠XRU = 75° and ∠RUY = 120°.
(iii) Cut off RT = 3.5 cm and UE = 4 cm.
(iv) Join TE.
(v) TRUE is the required quadrilateral.