Class 6

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 Playing With Numbers Ex 3.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 Playing With Numbers Exercise 3.3

Question 1.
Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say yes or no) :
(i) 128 (ii) 990 (ii) 1586 (iv) 275 (iv) 6686
(vi) 639210 (vii) 429714 (viii) 2856 (ix) (x) 40GS39
Solution:

Question 2.
Using divisibility tests, deter¬mine which of the following numbers are divible by 4 ; by 8 :
(a) 572 (b) 726352
(c) 5500 (d) 6000
(e) ^2159 (f) 14560
(g) 21084 (h) 31795072
(i) 1700 (j) 2150
Solution:
(a) 572, since the number formed by the last two digits is divisible by 4, hence it is divisible by 4; 572, since the nurtiber formed by the last three digits is not divisible by 8, hence it is not divisible by 8.
(b) 726352, since the number formed by the last two digits is divisible by 4, hence it is divisible by 4.
726352, since the number formed by the last three digits is divisible by 8, hence it is divisible by 8.
(c) 5500, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
5500, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(d) 6000, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
6000, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(e) 12159, since the number formed by the last two digits are not divisible by 4, hence it is not divisible by 4.
12159, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8. .
(f) 14560, since the number formed by the last twp digits are divisible by 4, hence it is divisible by 4.
14560, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(g) 21084, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
21084, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(h) 31795072, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
31795072, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(i) 1700, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
1700, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(j) 2150, since the number formed by the last two digits are not divisible by 4, hence it is not divisible by 4.
2150, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.

Question 3.
Using divisibility tests, deter¬mine which of the following numbers are
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 17852.
(j) 639210
Solution:
(a) 297144, since last digit is 4,
∴ It is divisible by 2.
Sum of the digits = 2 + 9 + 7 + 1 + 4 + 4 = 27, which is a multiple of 3,
∴ It is divisible by 3.
Since 297144 is divisible by both 2 and 3, hence it is divisible by 6.

(b) 1258, since last digit is 8, It is divisi-ble by 2. Sum of the digits =1 + 2 + 5 + 8 = 16, which
is not a multiple of 3, .∴ It is not divisible by 3.
Hence, 1258 is not divisible by 6.

(c) 4335, since last digit is 5,
∴ It is not divisible by 2.
Hence, 4335 is not divisible by 6.

(d) 61233, since last digit is 3,
∴ It is not divisible by 2.
Hence, 61233 is not divisible by 6.

(e) 901352, since last digit is 2,
∴ It is divisi-ble by 2.
Sum of the digits = 9 + 0 + 1 + 3 + 5 + 2 = 20,
which is not a multiple of 3,
∴ It is not divisible by 3.
Hence, 901352 is not divisible by 6.

(f) 438750, since last digit is 0,
∴ It is divisi¬ble by 2.
Sum of the digits = 4 + 3 + 8 + 7 + 5 + 0 = 27, which is a multiple of 3,
∴ It is divisible by 3. Since, 438750 is divisible by both 2 and 3,
hence it is divisible by 6.

(g) 1790184, since last digit is 4,
∴ It is divisible by 2.
Sum of the digits = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30, which is a multiple of 3,
∴ It is divisible by 3.
Since, 1790184 is divisible by both 2 and 3, hence it is divisible by 6.

(h) 12583, since last digit is 3,
∴ It is not divisible by 2.
Hence, 12583 is not divisible by 6.

(i) 639210, since last digit is 0,
∴ It is divisible by 2.
Sum of the digits = 6 + 3 + 9 + 2 + 1 + 0 = 21, which is a multiple of 3,
∴ It is divisible by 3.
Since 639210 is divisible by both 2 and 3, hence it is divisible by 6.

(j) 17852, since last digit is 2,
∴ It is divisible by 2.
Sum of the digits = 1 + 7 + 8 + 5 + 2 = 23, which is not a multiple of 3,
∴ It is not divisible by 3.
Hence, 17852 is not divisible by 6.

Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 11.
(a) 5545 (b) 10824 (c) 7138965 (d) 70169308 (e) 10000001 if) 901153.
Solution:

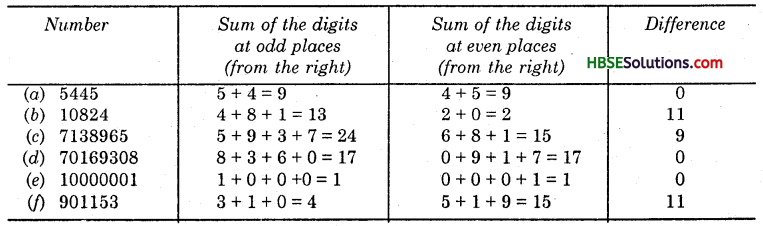
We observe that in each case except in (Hi), the difference is either 0 or divisible by 11. Hence, 5445, 10824,70169308, 10000001, 901153 are all divisible by 11, but 7138965 is not divisible by 11.

Question 5.
Write the (a) smallest digit, (6) largest digit in the blank space of each of the following numbers so that the number is divisible by 3 :
(a) ……………….. 6724, (b) 4765 …………….. 2.
Solution:
(a) 2 + 6 + 7 + 2 + 4 = 21, which is a multiple of 3.
8 + 6 + 7 + 2 + 4 = 27, which is a multiple of 3.
Hence, (a) smallest digit is 2 and (b) largest dig^ is 8.
(b) 4 + 7 + 6 + 5 + 0 + 2 = 24, which is a multiple of 3.
4 + 7 + 6 + 5 + 9 + 2 = 33, which is a multiple of 3.
Hence, (a) smallest digit is 0 and (b) largest digit is 9.

Question 6.
Write digit in the blank space of each of the following numbers so that the number is divisible by 11 :
(a) 92 ………….. 389 (6) 8……… 9484.
Solution:

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 Playing With Numbers Ex 3.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 Playing With Numbers Exercise 3.1

Question 1.
Write all the factors of the following numbers :
(a) 24 (b) 15 (c) 21
(d) 27 (e) 12 (f) 20
(g) 18 (h) 23 (i) 36
Solution:
(a) 24 = 1 x 24
= 2 x 12
= 3 x 8
= 4 x 6
∴ All the factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.

(b) 15 = 1 x 15
= 3 x 5
∴ All the factors of 15 are 1, 3, 5, 15. Ans.

(c) 21 = 1 x 21
= 3 x 7
∴ All the factors of 21 are 1, 3, 7, 21. Ans.

(d) 27 = 1 x 27
= 3 x 9
∴ All the factors of 27 are 1, 3, 9, 27. Ans.

(e) 12 = 1 x 12
= 2 x 6
= 3 x 4
∴ All the factors of 12 are 1, 2, 3, 4, 6, 12.

(f) 20 = 1 x 20
= 2 x 10 = 4 x 5
∴ All the factors of 20 are 1, 2, 4, 5, 10, 20.

(g) 18 = 1 x 18
= 2 x 9 = 3 x 6
∴ All the factors of 18 are 1, 2, 3, 6, 9, 18.

(h) 23 = 1 x 23
∴ All the factors of 23 are 1, 23.

(i) 36 = 1 x 36
= 2 x 18 = 3 x 12 = 4 x 9 = 6 x 6
∴ All the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.

Question 2.
Write the first five multiples of:
(a) 5 (b) 8 (c) 9
Solution:
(a) The required multiples of 5 are :
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25.
i.e., 5, 10, 15, 20 and 25

(b) The required multiples of 8 are :
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40.
i.e., 8, 16, 24, 32 and 40

(c) The required multiples of 9 are :
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45.
i.e., 9, 18, 27, 36 and 45.

Question 3.
Match the items in column 1 with the items in column 2 :
Column 1 — Column 2
(i) 35 — (a) Multiple of 8
(ii) 15 — (b) Multiple of 7
(iii) 16 — (c) Multiple of 70
(iv) 20 — (d) Factor of 30
(v) 25 — (e) Factor of 50
(f) Factor of 20
Solution:
(i) – (b) Multiple of 7
(ii) – (d) Factor of 30
(iii) – (a) Multiple of 8
(iv) – (f) Factor of 20
(v) – (e) Factor of 50

Question 4.
Find all the multiples of 9 upto 100.
Solution:
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99.
Hence all the multiples of 9 upto 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and 99.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 Playing With Numbers Ex 3.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 Playing With Numbers Exercise 3.2

Question 1.
What is the sum of any two (a) odd numbers and (b) even numbers ?
Solution:
(a) The sum of any two odd numbers is even and
(b) Sum of any two even numbers is also even.

Question 2.
State whether the following statements are true of false :
(a) The sum of three odd numbers is even.
(b) The sum of t wo odd numbers and one even number is even.
(c) The product of three odd numbers is odd.
(d) If an even number is divided by 2, the quotient is always odd.
(e) All prime num bers are odd.
(f) Prime numbers do not. have any factors.
(g) Sum of two prime numbers is always even.
(h) 2 is the only even prime number.
(i) All even numbers are composite numbers.
(j) The product of two even numbers is always even.
Solution:
(a) F (b) T (c) T (d) F (e) F (f) F (g) F (h) T (i) F (j) T.

Question 3.
The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.
Solution:
17 and 71; 37 and 73; 79 and 97 are such pairs of prime numbers upto 100.

Question 4.
Write down separately the prime and composite numbers less that 20.
Solution:

Prime numbers less than 20 are: 2, 3, 5, 7, 11, 13, 17, 19.
Composite numbers less than 20 are: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18.

Question 5.
What is the greatest prime number between 1 and 10 ?
Solution:

7 is the greatest prime number between 1 and 10.

Question 6.
Express the following as the sum of two odd primes :
(a) 44
(b) 36
(c) 24
(d) 18
Solution:
(a) 44 = 13 + 31 = 3 + 41
(b) 36 = 13 + 23 = 5 + 31
(c) 24 = 11 + 13 = 5 + 19
(d) 18 = 5 + 13 = 7 + 11.

Question 7.
Give three pairs of prime numbers whose difference is 2.
[Remark : Two prime numbers whose difference is 2 are called twin primes].
Solution:
(i) (3, 5) (ii) (5, 7) (iii) (11, 13).

Question 8.
Which of the following numbers are prime ?
(a) 23
(b) 51
(c) 37
(d) 26.
Solution:
23 and 37 are prime numbers.

Question 9.
Write seven consecutive com¬posite numbers less than 100- so that there is no prime number between them.
Solution:
90, 91, 92, 93, 94, 95 and 96.

Question 10.
Express each of the following numbers as the sum of three odd primes:
(a) 21
(b) 31
(c) 53
(d) 61.
Solution:
(a) 21 = 3 + 5 + 13
(b) 31 = 3 + 5 + 23
(c) 53 = 3 + 7 + 43
(d) 61 = 3 + 5 + 53 = 7 + 13 + 41

Question 11.
Write five pairs of prime numbers below 20 whose sum is divisible by 5.
Solution:
(i) 2 + 3 = 5
(ii) 3 + 7 = 10
(iii) 2 + 13 = 15
(iv) 3 + 17 = 20
(v) 7 + 13 = 20.

Question 12.
Fill in the blanks in the following:
(a) A number which has only two factors is called a ……………
(b) A number which has more than two factors is called a ……………
(c) 1 is neither …………… nor ……………
(d) The smallest prime number is ……………
(e) The smallest composite number is ……………
(f) The smallest even number is ……………
Solution:
(a) Prime number
(b) Composite number.
(c) Prime, Composite
(d) 2
(e) 4
(f) 2.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 2 Whole Numbers Exercise 2.3

Question 1.
Which of the following will not represent zero:
(a) a + 0
(b) 0 x 0
(c) \(\frac{0}{2}\)
(d) \(\frac{10-10}{2}\)
Solution:
(a) 1 + 0 = 1
(b) 0 x 0 = 0
(c) \(\frac{0}{2}\) = 0
(d) \(\frac{10-10}{2}\) = \(\frac{0}{2}\) = 0
∴ (a) will not represent zero.

Question 2.
If the product of two whole numbers is zero, can we say that one or both of them will be zero ? Justify through e × amples.
Solution:
One of them is zero i.e., 0 × 2 = 0
Both of them are zero i.e., 0 × 0 = 0.

Question 3.
If the product of two whole numbers is 1, can we say that one or both of them will be 1 ? Justify through an e × ample.
Solution:
Both of them will be one i.ef,
1 × 1 = 1.

Question 4.
Find by distributivity method :
(a) 728 × 101
(e) 824 × 25
(e) 504 × 35.
(b) 5437 × 1001
(d) 4275 × 125
Solution:
(a) 728 × 101
728 × (100 + 1)
= 728 × 100 + 728
= 72800 + 728
= 73528

(b) 5437 × 1001
5437 × (1000 + 1)
= 5437000 + 5437
= 5442437

(c) 824 x 25 = 824 x \(\frac{100}{4}\)
\(\frac{824}{4}\) x 100 = 20600

(d) 4275 × 125
= 4275 × (100 + 25)
= 427500 + 4275 × 25
= 427500 + 106875
= 534375

(e) 504 × 35
= (500 + 4) × 35
= 500 × 35 + 4 × 35
= 17500 + 140
= 17640

Haryana State Board HBSE 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 2 Whole Numbers Exercise 2.2

Question 1.
Find the sum by suitable rearrangement :
(a) 837 + 208 + 363
(b) 1962 + 453 + 1538 + 647.
Solution:
(a) 837 + 208 + 363
= (837 + 363) + 208 = 1200 + 208 = 1408
(b) 1962 + 453 + 1538 + 647
= (1962 + 1538) + (453 + 647) = 3500 + 1100 = 4600

Question 2.
Find the product by a suitable rearrangement :
(a) 2 × 1768 × 50
(b) 4 × 166 × 25
(c) 8 × 291 × 125
(d) 625 × 279 × 16
(e) 285 × 5 × 60
(f) 125 × 40 × 8 × 25.
Solution:
(a) 2 × 1768 × 50
= (2 × 50) × 1768 = 100 × 1768 = 176800
(b) 4 × 166 × 25
= (4 × 25) × 166 = 100 × 166 = 16600
(c) 8 × 291 × 125
= (8 × 125) × 291 = 1000 × 291 = 291000
(d) 625 × 279 × 16
= (625 × 16) × 279 = 10000 × 279 ‘ = 2790000
(e) 285 × 5 × 60
= 285 × (5 × 60)
= 285 × 300 = 85500
(f) 125 × 40 × 8 × 25
= (125 × 8) × (40 × 25)
= 1000 × 1000 = 1000000

Question 3.
Find the value of the following :
(a) 297 × 17 + 297 × 3
(b) 54279 × 92 + 8 × 54279
(c) 81265 × 169 – 81265 × 69
(d) 3845 × 5 × 782 + 769 × 25 × 218.
Solution:
(a) 297 × 17 + 297 × 3
= 297 × (17 + 3)
= 297 × 20 = 5940 Ans.
(b) 54279 × 92 + 8 × 54279
= 54279 × (92 + 8)
= 54279 × 100 = 5427900
(c) 81265 × 169 – 81265 × 69
= 81265 (169 – 69)
= 81265 × 100 = 8126500
(d) 3845 × 5 × 782 + 769 × 25 × 218
= (769 × 5) × 5 × 782 + 769 × 25 × 218
= 769 × (5 × 5) × 782 + 769 × 25 × 218
= 769 × 25 × 782 + 769 × 25 × 218
= 769 × 25 × (782 + 218)
= 769 × 25 × 1000 = 19225000

Question 4.
Find the product, using suitable properties :
(a) 738 × 103
(b) 854 × 102
(c) 258 × 1008
(d) 1005 × 168.
Solution:
(a) 738 × 103
= 738 × (100 + 3)
= 738 × 100 + 738 × 3
= 73800 + 2214
= 76014

(b) 854 × 102 = 854 × (100 + 2)
= 854 × 100 + 854 × 2
= 85400 + 1708
= 87108.

(c) 258 × 1008
= 258 × (1000 + 8)
= 258 × 1000 + 258 × 8
= 258000 + 2064
= 260064.

(d) 1005 × 168 = (1000 + 5) × 168
= 1000 × 168 + 5 × 168
= 168000 + 840
= 168840.

Question 5.
A ta × i-driver filled his car petrol tank with 40 litres of petrol on Monday. The ne × t day, he filled the tank with 50 litres of petrol. If the petrol costs Rs. 44 per litre, how much did he spend in all on petrol ?
Solution:
Method-1:
Cost of 40 litres of petrol
= Rs. 44 × 40
= Rs. 1760
Cost of 50 litres of petrol
= Rs. 44 × 50
= Rs. 2200
∴ Total cost = Rs. (1760 + 2200)
= Rs. 3960.

Method-2 :
Petrol purchased on Monday = 40 litres
Petrol purchased on ne × t day = 50 litres
Total petrol purchased
= (40 + 50) l = 90 l
∴ Total cost = Rs. 44 × 90
= Rs. 3960.

Question 6.
A vendor supplies 32 litres of milk to a hotel in the morning and 68 litres of milk in the evening. If the milk costs Rs. 15 per litre, how much money is due to the vendor per day ?
Solution:
Milk supplied in the morning = 32 litres
Milk supplied in the evening Milk supplied in one day = 68 litres
∴ Milk supplied in one day = (32 + 68)l = 100 l
Hence, total cost of milk per day = Rs. 15 × 100 = Rs. 1500

Question 7.
Match the following :
(i) 425 × 136 = 425 × (6 + 30 + 100) — (a) Commutativity under multiplication.
(ii) 2 × 49 × 50 = 2 × 50 × 49 — (b) Commutativity under addition.
(Hi) 80 + 2005 + 20 = 80 + 20 + 2005 — (c) Distributivity of multiplication over addition.
Solution:
(i)—(c),
(ii)—(a),
(iii)—(b).

Haryana State Board HBSE 6th Class Hindi Solutions Hindi Vyakaran kriya क्रिया Exercise Questions and Answers.

Haryana Board 6th Class Hindi Vyakaran क्रिया

क्रिया का अर्थ है- ‘काम’। काम या तो होता है या किया जाता है।

परिभाषा- क्रिया वह विकारी शब्द है जिससे काम के करने या होने का बोध होता है।
क्रिया के मूल रूप को धातु (Root) कहते हैं। क्रिया के रूप धातु से बनते हैं। जैसे –
‘खा’ धातु से – खाऊँगा, खाता, खाऊँ, खाई आदि।
इसी प्रकार ले, दे, जा, पढ़ आदि धातुओं से विभिन्न क्रिया-रूप बनते हैं।

क्रिया के भेद (Kinds of Verb) :
मुख्य रूप से क्रिया के दो भेद हैं-
1. अकर्मक क्रिया (Intransitive Verb)
2. सकर्मक क्रिया (Transitive Verb)

1. अकर्मक क्रिया (Intransitive Verb) :
जिन क्रियाओं में कर्म की आवश्यकता नहीं होती, उन्हें सकर्मक क्रियाएँ कहा जाता है। ऐसे वाक्यों में क्रिया के व्यापार का फल कर्ता में ही रहता है। जैसे-
स्वाति दौड़ती है। बच्चा रोता है।
इन वाक्यों में ‘स्वाति’ और ‘बच्चा’ कर्ता हैं तथा ‘दौडना’ और ‘रोना’ क्रियाएँ हैं। इनके साथ कर्म है ही नहीं और न उसकी आवश्यकता है।

2. सकर्मक क्रिया (Transitive Verb):
जिन क्रियाओं के व्यापार का फल सीधे कर्म पर पड़ता है, उन्हें सकर्मक क्रिया कहते हैं। कर्म के बिना ये वाक्य अधूरे प्रतीत होते हैं। जैसे-
मैंने खाया। (क्या खाया ?)
मैंने आम खाया। (आम-कर्म)
दूसरा वाक्य पूरा है तथा इसकी क्रिया ‘खाया’ सकर्मक है।

सकर्मक क्रिया की पहचान कर्ता और क्रिया के बीच ‘क्या’ और ‘किसे’ आदि प्रश्न करने से हो जाती है। यदि प्रश्न का उत्तर मिले तो क्रिया सकर्मक और न मिले तो क्रिया अकर्मक होती है।
जैसे- वह दूध पीता है।
प्रश्न – वह क्या पीता है ?
उत्तर – दूध। अतः ‘पीता है’ क्रिया सकर्मक है।

द्विकर्मक क्रिया : द्विकर्मक क्रिया वाले वाक्यों में दो-दो कर्म होते हैं। इनमें पहला कर्म प्रायः प्राणीवाचक होता है। इसे ‘गौण कर्म’ कहते हैं। दूसरा कर्म प्रायः अप्राणीवाचक होता है और यह मुख्य कर्म कहलाता है।
मुख्य कर्म विभक्ति-चिह्न (परसर्ग) रहित होता है और गौण कर्म के साथ प्रायः ‘को’ परसर्ग लगता है।
उदाहरण :
मैं राम को पत्र लिखता हूँ। इस वाक्य में दो कर्म हैं-
(i) राम को – प्राणीवाचक – गौण कर्म।
(ii) पत्र – अप्राणीवाचक – मुख्य कर्म।

संरचना की दृष्टि से क्रिया के पांच भेद हैं :
1. सामान्य क्रिया (Ordinary Verb)
2. संयुक्त क्रिया (Compound Verb)
3. नामधातु क्रिया (Nominal Verb)
4. प्रेरणार्थक क्रिया (Causal Verb)
5. पूर्वकालिक क्रिया (Absolutive Verb)

1. सामान्य क्रिया : इसमें केवल क्रिया का प्रयोग किया जाता है।
जैसे- राम गया, मैंने पढ़ा।

2. संयुक्त क्रिया : इसमें दो या दो से अधिक क्रियाओं को मिलाकर प्रयोग किया जाता है। जैसे
मैं खाना खा चुका हूँ। – वह अब सो गया है।

3. नामधातु क्रिया : संज्ञा, सर्वनाम, विशेषण आदि से बनी क्रियाएं नामधातु क्रिया कहलाती हैं। जैसे-
संज्ञा से- बात-से ‘बतियाना’, हाथ-से ‘हथियाना’। सर्वनाम से- मैं-से ‘मिमियाना’ ; अपना-से ‘अपनाना’। विशेषण से- गर्म-से ‘गर्माना’ ; नरम-से ‘नरमाना’।

4. प्रेरणार्थक क्रिया : जब कर्ता स्वयं कार्य न करके किसी अन्य को प्रेरणा देकर काम करवाता है, तब क्रिया का वह रूप प्रेरणाथक क्रिया कहलाता है। जैसे-

[वास्तव में द्वितीय कोटि की प्रेरणार्थक क्रियाएँ ही सही अर्थों में प्रेरणार्थक क्रियाएँ हैं।]

5. पूर्वकालिक क्रिया : मुख्य क्रिया से पूर्व होने वाली क्रिया पूर्वकालिक क्रिया कहलाती है। जैसेवह दूध पीकर चला गया। मैं नहाकर पुस्तक पढूंगा।

अभ्यास

1. अन्तर स्पष्ट करो:

(क) धातु और क्रिया में।
(ख) अकर्मक और सकर्मक क्रिया में।
(ग) सामान्य और संयुक्त क्रिया में।

2. नीचे लिखे वाक्यों में प्रयुक्त क्रियाओं के नीचे रेखा खींचो :

(क) सोहन ने खाना खाया।
(ख) वह अपनी जगह से उठ गया।
(ग) दिव्या पुस्तक पढ़ रही है।
(घ) बालक खेलकर सो गया।

3. इन वाक्यों में से अकर्मक और सकर्मक क्रियाएं छांटकर तालिका लिखें :

(क) वह हंस रहा है।
(ख) वह पत्र लिख रहा है।
(ग) दूध उबल रहा है।
(घ) भारती दूध उबाल रही है।
(ङ) मैंने पुस्तक पढ़ी।
(च) बालक चिल्लाया

4. तीन मूल धातुएं लिखकर उनसे दो-दो क्रिया-रूप बनाकर लिखो।

Haryana State Board HBSE 6th Class Hindi Solutions Hindi Vyakaran Avyay (Avikaari Shabd) अव्यय (अविकारी शब्द) Exercise Questions and Answers.

Haryana Board 6th Class Hindi Vyakaran अव्यय (अविकारी शब्द)

अव्यय (अविकारी शब्द):
हमने संज्ञा, सर्वनाम, विशेषण और क्रिया पदों का अध्ययन किया और देखा कि इन पदों के रूपों में परिवर्तन होता है, अत: इन्हें विकारी पद कहते हैं। अब उन पदों का अध्ययन किया जाएगा जिनका रूप सदैव एक ही बना रहता है और उनमें परिवर्तन नहीं होता। एक ही रूप बने रहने के कारण इन्हें अव्यय कहते हैं। अव्यय शब्द का अर्थ है जिसका व्यय न हो अर्थात् जिनमें विकार न आए। इन्हें अविकारी पद भी कहते हैं।

अव्यय वे शब्द हैं जिनमें लिंग, वचन, पुरुष, काल आदि से मिलकर विकार या रूप-परिवर्तन नहीं होता।।

अव्यय के भेद (Indeclinable Words) :
अव्यय के पांच मुख्य भेद माने जाते हैं-
1. क्रिया विशेषण (Adverb)
2. संबंधबोधक (Post Position)
3. समुच्चयबोधक (Conjunction)
4. विस्मयादिबोधक (Interjection)
5. निपात (Stress)

1. क्रिया विशेषण (Adverb) :
जो पद क्रिया की विशेषता बताता है उसे क्रिया विशेषण अव्यय कहते हैं ; जैसेधीरे-धीरे, आजकल, के पास, बिल्कुल।
क्रिया विशेषण के चार भेद माने गए हैं :
(क) कालवाचक क्रियाविशेषण (Adverb of Time) : जो पद क्रिया के काल या समय की विशेषता बताता है उसे कालवाचक क्रियाविशेषण कहते हैं; जैसे

• तुम चेन्नै कब जाओगे।
• संजय परसों जयपुर से आया था।
• शीला प्रतिदिन स्कूल जाती है।
• महँगाई आजकल बढ़ती जा रही है।

(ख) स्थानवाचक क्रियाविशेषण (Adverb of Place): जो पद क्रिया के स्थान का बोध कराता है, उसे स्थानवाचक क्रियाविशेषण कहते हैं; जैसे-

• वह यहां रहता है।
• माता जी बाहर गई हैं।
• तुम इधर-उधर मत जाओ।
• वर्षा में कहां जाओगे ?

(ग) रीतिवाचक क्रियाविशेषण (Adverb of Manner): जो पद क्रिया के होने की रीति या विधि संबंधी विशेषता बताता है, उसे रीतिवाचक क्रियाविशेषण कहते हैं ; जैसे-

• कार तेज़ दौड़ती है।
• साइकिल धीरे-धीरे चलती है।
• मुदिता ध्यानपूर्वक पढ़ती है।

(घ) परिमाणवाचक क्रियाविशेषण (Adverb of Quantity) : जो पद क्रिया की मात्रा या परिमाण बताए, वह परिमाणवाचक क्रियाविशेषण है; जैसे

• मैं बिल्कुल थक गया हूँ।
• बंगाल में चावल अधिक खाया जाता है।
• थोड़ा खाओ, खूब चबाओ।

2. संबंधबोधक अव्यय (Post Position) :
संबंधबोधक अव्यय अपने पूर्वपद के साथ संबध जोड़ता है। इस पद के पहले किसी-न-किसी परसर्ग की अपेक्षा रहती है; जैसे- से दूर, के साथ, के कारण, के वास्ते, की अपेक्षा, की जगह, के अनुसार, की तरफ। उदाहरण के लिए :

• मैं घर से दूर पहुंच गया था।
• इस मकान के पीछे शिव मंदिर है।
• मोहन बाज़ार की ओर गया है।
• उसके सामने तुम कहीं नहीं ठहर सकते।

3. समुच्चयबोधक अव्यय (Conjunction) :
जो अव्यय पदों, पदबंधों और उपवाक्यों को जोड़ते हैं, उन्हें समुच्चयबोधक अव्यय कहते हैं; जैसे- और, कि, अथवा, क्योंकि, इसलिए।
समुच्चयबोधक अव्यय के दो भेद हैं :
(क) समानाधिकरण समुच्चयबोधक : जो दो या उससे अधिक समान पदों, पदबंधों, उपवाक्यों को जोड़ता है, वह समानाधिकरण समुच्चयबोधक अव्यय कहलाता है। जैसे-

• नरेन्द्र शाम को रोटी और दाल खाता है।
• जोगेन्द्र रसमलाई या गुलाबजामुन खाता है।

(ख) व्यधिकरण समुच्चबोधक : जो पद किसी वाक्य के एक या अधिक आश्रित उपवाक्यों को जोड़ता है, वह व्यधिकरण समुच्चयबोधक अव्यय कहलाता है; जैसे-

• शेख घर चला गया है क्योंकि उसके सिर में दर्द था।
• उसने परिश्रम किया फिर भी सफल नहीं हो पाया।

4. विस्मयादिबोधक अव्यय (Interjection) :
विस्मयादिबोधक अव्यय वे रूप हैं जो आश्चर्य, हर्ष, शोक, व्यथा, घृणा आदि मनोभावों के उद्गार को व्यक्त करते हैं। उद्गार प्रायः अपने-आप मुँह से निकल जाते हैं और इनका उद्देश्य प्रायः सुनने वाले को कोई सूचना देना नहीं होता; जैसे-

• वाह ! क्या सुंदर दृश्य है। (आश्चर्य)
• अरे ! गाड़ी से बचो। (चेतावनी)
• क्या बोलूँ ! (व्यथा)
• शाबाश ! बहुत बड़ा काम किया तुमने। (प्रशंसा)
• छिः ! ऐसी गंदी बात करता है। (घृणा)

5. निपात (Stress) :
वाक्य में जो अव्यय किसी शब्द या पद के बाद लगकर उसके अर्थ में विशेष प्रकार का बल या भाव पैदा करने में सहायता करते हैं, उन्हें निपात या अवधारणामूलक शब्द कहते हैं; जैसे
1. राम ही कल जाएगा।
2. राम कल ही जाएगा।
3. कल राम भी जाएगा।
4. मैंने तो कुछ नहीं किया।
5. तुम्हारे बारे में बच्चे तक जानते हैं।

अभ्यास

1. अव्यय किसे कहते हैं ? उदाहरण देकर स्पष्ट कीजिए।
2. अव्यय के भेद बताते हुए प्रत्येक के दो-दो उदाहरण दीजिए।
3. क्रिया विशेषण का अर्थ स्पष्ट करते हुए इसके प्रकारों का विवेचन उदाहरण सहित कीजिए।
4. निम्नलिखित अनुच्छेद में प्रयुक्त अव्ययों के नीचे रेखा खींचो तथा उसका भेद भी बताओ।
राम और श्याम तेज दौड़ रहे थे। वे पेड़ के पास रुक गए। अरे ! इतना लंबा सांप कहां से आ गया ? राम बोला कि मैं अब नहीं दौडूंगा। श्याम भी चला गया।
5. क्रिया-विशेषण छांटो :

• गीता मधुर गाती है।
• वह ऊपर बैठा है।
• रवि आज आएगा।

6. संबंधबोधक छांटो:

• पेड़ के नीचे विश्राम कर लो।
• गाँव के परे एक मठ है।
• भवन के ऊपर झंडा फहरा रहा है।
• सेना के आगे घुड़सवार थे।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 2 Whole Numbers Exercise 2.1

Question 1.
Write the next three natural numbers after 10,999.
Solution:
After 10,999 next three natural numbers are :
10,999 + 1 = 11,000
11,000 + 1 = 11,001
and 11,001 + 1 = 11,002.

Question 2.
Write the three whole numbers occurring just before 10,001.
Solution:
Before 10,001 three whole numbers are :
10,001 – 1 = 10,000
10,000 – 1 = 9,999
and 9,999 – 1 = 9,998.

Question 3.
Which is the smallest whole number ?
Solution:
Zero is the smallest whole number.

Question 4.
How many whole numbers are there between 32 and 53 ?
Solution:
There are 20 whole numbers between 32 and 53.

Question 5.
Write the successor of:
(a) 24,40,701
(b) 1,00,199
(c) 10,99,999
(d) 23,45,670.
Solution:
(a) Successor of 24,40,701 is 24,40,701 + 1 = 24,40,702.
(b) Successor of 1,00,199 is 1,00,199 + 1 = 1,00,200.
(c) Successor of 10,99,999 is 10,99,999 + 1 = 11,00,000.
(d) Successor of 23,45,670 is 23,45,670 + 1 = 23,45,671.

Question 6.
Write the predecessor of:
(a) 94
(b) 10,000
(c) 2,08,090
(d) 76,54,321.
Solution:
(a) Predecessor of 94 is 94 – 1 = 93.
(b) Predecessor of 10,000 is 10,000 – 1 = 9,999.
(c) Predecessor of 2,08,090 is 2,08,090 – 1 = 2,08,089.
(d) Predecessor of 76,54,321 is 76,54,321 – 1 = 76,54,320.

Question 7.
In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also write them with the appropriate sign (>, <) between them.
(a) 530, 503
(b) 370, 307
(c) 98765, 56789
(d) 9830415, 10023001.
Solution: (a) 503 is on the left to 530.
∴ 503 < 530 or 530 > 503.
(b) 307 is on the left to 370.
∴ 307 < 370 or 370 > 307. ,
(c) 56789 is on the left to 98765.
∴ 56789 < 98765 or 98765 > 56789.
(d) 9830415 is on the left to 10023001.
∴ 9830415 < 10023001 or 10023001 > 9830415.

Question 8.
Which of the following state¬ments are true (T) and which are false (F)?
(a) Zero is the smallest natural number.
(b) 400 is the predecessor of 399.
(c) Zero is the smallest whole number.
(d) 600 is the successor of 599.
(e) All natural numbers are whole numbers.
(f) All whole numbers are natural numbers.
(g) The predecessor of a two digit number is never a single digit number.
(h) One is the smallest whole number.
(i) The natural number 1 has no predecessor.
(j) The whole number 1 has no predecessor.
(k) The whole number 13 lies between 11 and 12.
(l) The whole number ‘0’ has no predecessor.
(m) The successor of a two-digit number is always a two-digit number.
Solution:
(a) F,
(b) F,
(c) T,
(d) T,
(e) T,
(f) F,
(g) F,
(h) F,
(i) T,
(j) F,
(k) F,
(l) T,
(m) F.

Haryana State Board HBSE 6th Class Hindi Solutions Hindi Vyakaran Vakya Vichar वाक्य विचार Exercise Questions and Answers.

Haryana Board 6th Class Hindi Vyakaran वाक्य विचार

मनुष्य अपने भावों या विचारों को वाक्य में ही प्रकट करता है। वाक्य में शब्दों का निश्चित क्रम होता है। कभी-कभी एक शब्द को भी वाक्य के रूप में प्रयुक्त किया जाता है। जैसे-

• राकेश – शशंक, तुम कहां जा रहे हो ?
• शशांक – स्कूल।

यहां शशांक ने केवल ‘स्कूल’ कहकर उत्तर दिया है।

वाक्य के अंग (Parts of Sentence) : वाक्य के दो अंग होते हैं :
1. उद्देश्य (Subject)
2. विधेय (Predicate)

1. उद्देश्य (Subject) : वाक्य में जिसके बारे में कुछ कहा जाता है, उसे उद्देश्य कहते हैं। जैसे-

• मोहन खेलता है।
• पक्षी डाल पर बैठा है।

इन वाक्यों में ‘मोहन’ और ‘पक्षी’ उद्देश्य हैं।

2. विधेय (Predicate) : उद्देश्य के विषय में जो कुछ – कहा जाता है, उसे विधेय कहते हैं। जैसे-

• मोहन खेलता है।
• पक्षी डाल पर बैठा है।

इन वाक्यों में ‘खेलता है’ और ‘डाल पर बैठा है’ विधेय हैं।

यह भी जानें : उद्देश्य में कर्ता मूल होता है तथा कभी-कभी उसका विस्तार भी किया जाता है। जैसे-
मेरा पुत्र मोहन खेलता है।
यहाँ भी कर्ता ‘मोहन’ ही है। पर ‘मेरा पुत्र’ कर्ता का विस्तार है।

विधेय में क्रिया मूल होता है। सकर्मक क्रिया में कर्म भी विधेय का विस्तार ही अंश होता है। कर्म और क्रिया दोनों का विस्तार ‘विधेय का विस्तार’ कहलाता है। जैसे-

• मोहन पत्र लिखता है।
• मोहन लंबा पत्र लिखता है।
• मोहन लंबा पत्र नित्य लिखता है।

इन तीनो वाक्यों में रेखांकित अंश विधेय हैं। दूसरे और तीसरे वाक्यों में विधेय का विस्तार किया गया है।

निम्नलिखित वाक्यों में उद्देश्य और विधेय की ओर ध्यान दीजिए :

वाक्य-रचना (Construction of Sentence):
वाक्य शब्दों या पदों का मात्र समूह नहीं होता है। प्रत्येक वाक्य में प्रयुक्त प्रत्येक पद किसी-न-किसी संबंध से परस्पर जुड़ा रहता है। यह संबंध ही पदों के समूह को वाक्य का रूप प्रदान करता है। इस संबंध को दो प्रकार से समझा जा सकता है।
1. पदक्रम और
2. अन्विति। वाक्य-रचना की दृष्टि से ये दोनों तत्त्व अनिवार्य हैं। ॥

वाक्य के भेद (Kinds of Sentence) :
(क) अर्थ के आधार पर वाक्य के आठ भेद हैं :
1. विधानवाचक (Assertive) : इसमें क्रिया करने का सामान्य कथन होता है।
जैसे- सौरभ पढ़ता है।
2. निषेधवाचक (Negative) : इसमें किसी कार्य के न होने का भाव प्रकट होता है।
जैसे- वह आज काम नहीं करेगा।

3. प्रश्नवाचक (Interrogative) : इस वाक्य में प्रश्न के पूछे जाने का बोध होता है।
जैसे- वह क्या कर रहा है?

4. आज्ञावाचक (Command or Order) : इसमें आज्ञा या अनुमति देने का भाव होता है।
जैसे- तुम अभी चले जाओ। (आज्ञा)
अब आप जा सकते हैं। (अनुमति)

5. संदेहवाचक (Doubr) : इस प्रकार के वाकय में किसी कार्य के होने के बारे में संदेह प्रकट किया जाता है।
जैसे- वह शायद ही यह काम करे।

6, इच्छावाचक (Will or Hope) : इस प्रकार के वाक्यों में वक्ता की इच्छा, आशीर्वाद, शुभकामना आदि का बोध होता है।
जैसे- ईश्वर तुम्हें दीर्घायु बनाए।

7. संकेतवाचक (Conditional) : इस वाक्य में एक क्रिया दूसरी पर निर्भर होती है।
जैसे- यदि वर्षा होती तो फसल अच्छी होती।

8. विस्मयादिवाचक (Exclamatory) : इन वाक्यों में घृणा, शोक, हर्ष, विस्मय आदि के भाव प्रकट होते हैं।
जैसे :

• वाह ! तुमने तो कमाल कर दिया।
• छिः छि कितनी गंदी जगह है ?

रचना के आधार पर वाक्य तीन प्रकार के होते हैं :
1. सरल वाक्य (Simple Sentence)
2. संयुक्त वाक्य (Compound Sentence)
3. मिश्र वाक्य (Complex Sentence)

1. सरल वाक्य (Simple Sentence) : जिस वाक्य में एक – उद्देश्य और एक विधेय हो उसे सरल या साधारण वाक्य कहते हैं। उदाहरण :

• लड़के खेल रहे हैं।
• तेज़ वर्षा हो रही है।

2. संयुक्त वाक्य (Compound Sentence) : समान स्तर के दो या अधिक सरल वाक्य जिस वाक्य में जुड़े हों, उसे संयुक्त वाक्य कहते हैं। उदाहरण :

• वर्षा हो रही है और धूप निकली हुई है।
• आप चाय लेंगे अथवा शर्बत मंगवाऊँ।

3. मिश्र वाक्य (Complex Sentence) : जिस वाक्य में एक सरल वाक्य (मुख्य उप वाक्य) हो तथा एक या अधिक आश्रित उपवाक्य हों, उसे मिश्र वाक्य कहते हैं। उदाहरण :

• उसने कहा कि मैं स्कूल जाऊंगा। (संज्ञा उपवाक्य)
• वह छात्र प्रथम आएगा, जो पीछे बैठा है। (विशेषण उपवाक्य)
• जब भी जाना चाहें, आप चले जाइए। (क्रिया विशेषण उपवाक्य)

आश्रित उपवाक्य तीन प्रकार के होते हैं :

1. संज्ञा उपवाक्य (Noun Clause)
2. विशेषण उपवाक्य (Adjective Clause)
3. क्रिया-विशेषण उपवाक्य (Adverb Clause)

1. संज्ञा उपवाक्य : जो उपवाक्य वाक्य में संज्ञा का काम करते हैं, वे संज्ञा उपवाक्य कहलाते हैं। इस उपवाक्य से पहले ‘कि’ का प्रयोग होता है और कभी-कभी ‘कि’ का लोप भी हो जाता है। जैसे-

• मुझे विश्वास है कि आप दीवाली हर घर जरूर आएँगे।
• तुम नहीं आओगे, मैं जानता था।

2. विशेषण उपवाक्य : विशेषण उपवाक्य मुख्य उपवाक्य में प्रयुक्त किसी संज्ञा की विशेषता बताता है। हिंदी में ‘जो’ (जिस, जिसे आदि) वाले उपवाक्य प्रायः विशेषण उपवाक्य होते हैं। जैसे

• आपकी वह पुस्तक कहां है, जो आप कल लाए
• जो आदमी पत्र बांटता है, वह डाकिया होता है।
• जिसे आप ढूंढ रहे हैं, वह मैं नहीं हूँ।
  अधिकतर विशेषण उपवाक्य के प्रारम्भ या अंत में प्रयुक्त होते हैं ; जैसे
• जो पैसे मुझे मिले थे, वे खर्च हो गए। (प्रारंभ में)
• वे पैसे खर्च हो गए, जो मुझे मिले थे। (अंत में)

3. क्रिया विशेषण उपवाक्य : यह उपवाक्य सामान्यत: मुख्य उपवाक्य की क्रिया की विशेषता बताता है। ये क्रिया विशेषण उपवाक्य किसी काल, स्थान, रीति, परिमाण, कार्य-कारण आदि का द्योतन करते हैं। इसमें जब, जहां, जैसा, ज्यों-ज्यों आदि समुच्चयबोधक अव्यय प्रयुक्त होते हैं; जैसे-

• जब बारिश हो रही थी, तब मैं घर में था। (कालवाची)
• जहाँ तुम पढ़ते थे, वहीं मैं पढ़ता था। (स्थानवाची)
• जैसा आप ने बताया था, वैसा मैंने किया। (रीतिवाची)

Haryana State Board HBSE 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.3

Question 1.
Estimate :
(a) 730 + 998
(b) 796-314
(c) 12,904 + 2,888
(d) 28,292 – 21,496.
Solution:
(a) We find 998 > 730.
Round off to hundreds

Actual answer = 730 + 998 = 1728
1728 is rounded to 1700.

(b) To begin with, we round off to hundreds

Actual answer = 796 – 314 = 482
482 is rounded to 500.

(c) We find 12,904 > 2,888
Round off to thousands
12,904 is rounded to 13,000
+2,888 is rounded to 3,000
∴ Estimated sum = 16,000
Actual answer = 12,904 + 2,888 = 15,792

(d) To begin with, we round off to thousands
28,292 is rounded to 28,000
-21,496 is rouned to 21,000
∴ Estimated difference = 7,000
Actual answer = 28,292 – 21496
= 6,796

Question 2.
Give a rough estimate (by round off to nearest hundreds) and also a closer estimate (by’rounding off to nearest tens):
(a) 439 + 334 + 4,317
(b) 1,08,734- 47,599
(c) 8,325 – 491
(d) 4,89,348 – 48,365.
Make four more of such examples.
Solution:
To begin with, we round off to thousands.
439 rounds to 0
334 rounds to 0
and 4,317 rounds to 4,000
Rough estimated sum= 0 + 0 + 4,000
= 4,000
This is not a reasonable estimate.
Actual sum = 439 + 334 + 4,317 = 5,090.
To get a closer estimate, let us try rounding off each number to hundreds.

(b) To begin with, we round off to ten thousands.

Actual difference = 1,08,734 – 47,599 = 61135
To get a closer estimate, let us try rounding off each number to hundreds.

(c) To begin with, we round off to hundreds

Actual difference = 8,325 – 491 = 7,834
To get a closer estimate let us try rounding off each number to tens.

This is a better and more meaningful estimate.

(d) To begin with, we round off to ten thousands

Actual difference = 4,89,348 – 48,365
= 4,40,983
To get a closer estimate, let us try rounding off each number to thousands.