Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 Playing With Numbers Ex 3.3 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 3 Playing With Numbers Exercise 3.3
Question 1.
Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say yes or no) :
(i) 128 (ii) 990 (ii) 1586 (iv) 275 (iv) 6686
(vi) 639210 (vii) 429714 (viii) 2856 (ix) (x) 40GS39
Solution:

![]()
Question 2.
Using divisibility tests, deter¬mine which of the following numbers are divible by 4 ; by 8 :
(a) 572 (b) 726352
(c) 5500 (d) 6000
(e) ^2159 (f) 14560
(g) 21084 (h) 31795072
(i) 1700 (j) 2150
Solution:
(a) 572, since the number formed by the last two digits is divisible by 4, hence it is divisible by 4; 572, since the nurtiber formed by the last three digits is not divisible by 8, hence it is not divisible by 8.
(b) 726352, since the number formed by the last two digits is divisible by 4, hence it is divisible by 4.
726352, since the number formed by the last three digits is divisible by 8, hence it is divisible by 8.
(c) 5500, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
5500, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(d) 6000, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
6000, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(e) 12159, since the number formed by the last two digits are not divisible by 4, hence it is not divisible by 4.
12159, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8. .
(f) 14560, since the number formed by the last twp digits are divisible by 4, hence it is divisible by 4.
14560, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(g) 21084, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
21084, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(h) 31795072, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
31795072, since the number formed by the last three digits are divisible by 8, hence it is divisible by 8.
(i) 1700, since the number formed by the last two digits are divisible by 4, hence it is divisible by 4.
1700, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
(j) 2150, since the number formed by the last two digits are not divisible by 4, hence it is not divisible by 4.
2150, since the number formed by the last three digits are not divisible by 8, hence it is not divisible by 8.
Question 3.
Using divisibility tests, deter¬mine which of the following numbers are
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 17852.
(j) 639210
Solution:
(a) 297144, since last digit is 4,
∴ It is divisible by 2.
Sum of the digits = 2 + 9 + 7 + 1 + 4 + 4 = 27, which is a multiple of 3,
∴ It is divisible by 3.
Since 297144 is divisible by both 2 and 3, hence it is divisible by 6.
![]()
(b) 1258, since last digit is 8, It is divisi-ble by 2. Sum of the digits =1 + 2 + 5 + 8 = 16, which
is not a multiple of 3, .∴ It is not divisible by 3.
Hence, 1258 is not divisible by 6.
(c) 4335, since last digit is 5,
∴ It is not divisible by 2.
Hence, 4335 is not divisible by 6.
(d) 61233, since last digit is 3,
∴ It is not divisible by 2.
Hence, 61233 is not divisible by 6.
(e) 901352, since last digit is 2,
∴ It is divisi-ble by 2.
Sum of the digits = 9 + 0 + 1 + 3 + 5 + 2 = 20,
which is not a multiple of 3,
∴ It is not divisible by 3.
Hence, 901352 is not divisible by 6.
(f) 438750, since last digit is 0,
∴ It is divisi¬ble by 2.
Sum of the digits = 4 + 3 + 8 + 7 + 5 + 0 = 27, which is a multiple of 3,
∴ It is divisible by 3. Since, 438750 is divisible by both 2 and 3,
hence it is divisible by 6.
(g) 1790184, since last digit is 4,
∴ It is divisible by 2.
Sum of the digits = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30, which is a multiple of 3,
∴ It is divisible by 3.
Since, 1790184 is divisible by both 2 and 3, hence it is divisible by 6.
(h) 12583, since last digit is 3,
∴ It is not divisible by 2.
Hence, 12583 is not divisible by 6.
(i) 639210, since last digit is 0,
∴ It is divisible by 2.
Sum of the digits = 6 + 3 + 9 + 2 + 1 + 0 = 21, which is a multiple of 3,
∴ It is divisible by 3.
Since 639210 is divisible by both 2 and 3, hence it is divisible by 6.
![]()
(j) 17852, since last digit is 2,
∴ It is divisible by 2.
Sum of the digits = 1 + 7 + 8 + 5 + 2 = 23, which is not a multiple of 3,
∴ It is not divisible by 3.
Hence, 17852 is not divisible by 6.
Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 11.
(a) 5545 (b) 10824 (c) 7138965 (d) 70169308 (e) 10000001 if) 901153.
Solution:
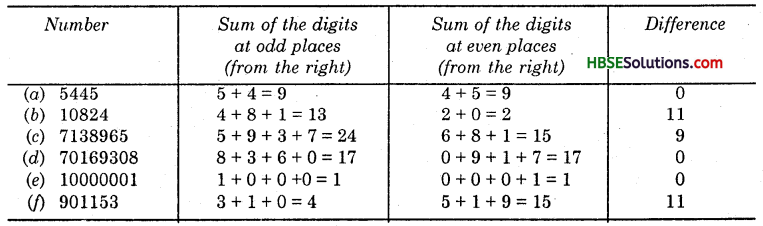
We observe that in each case except in (Hi), the difference is either 0 or divisible by 11. Hence, 5445, 10824,70169308, 10000001, 901153 are all divisible by 11, but 7138965 is not divisible by 11.
Question 5.
Write the (a) smallest digit, (6) largest digit in the blank space of each of the following numbers so that the number is divisible by 3 :
(a) ……………….. 6724, (b) 4765 …………….. 2.
Solution:
(a) 2 + 6 + 7 + 2 + 4 = 21, which is a multiple of 3.
8 + 6 + 7 + 2 + 4 = 27, which is a multiple of 3.
Hence, (a) smallest digit is 2 and (b) largest dig^ is 8.
(b) 4 + 7 + 6 + 5 + 0 + 2 = 24, which is a multiple of 3.
4 + 7 + 6 + 5 + 9 + 2 = 33, which is a multiple of 3.
Hence, (a) smallest digit is 0 and (b) largest digit is 9.
![]()
Question 6.
Write digit in the blank space of each of the following numbers so that the number is divisible by 11 :
(a) 92 ………….. 389 (6) 8……… 9484.
Solution:
