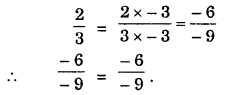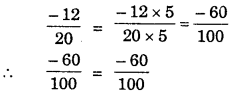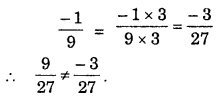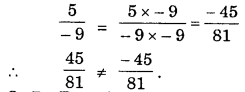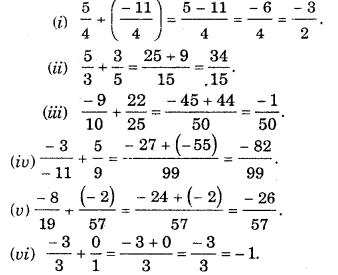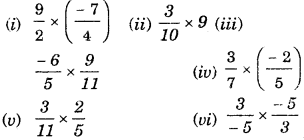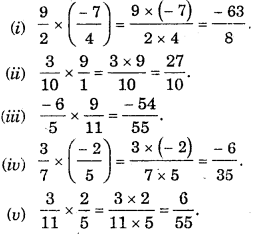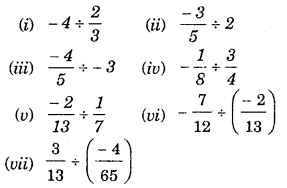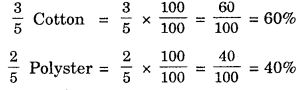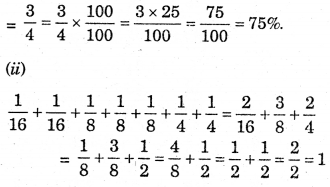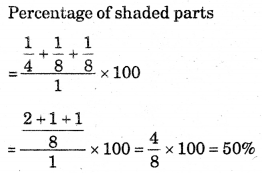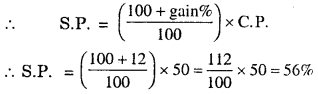Author name: Prasanna

Haryana State Board HBSE 7th Class Maths Solutions Chapter 9 Rational Numbers InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 9 Rational Numbers InText Questions

Question 1.
Is the number \(\frac{2}{-3}\) rational number ?
Solution:
\(\frac{2}{-3}\) is a rational number.

Question 2.
List ten rational numbers.
Solution:
\(\frac{5}{2}, \frac{-3}{2}, 5,4,-1,-2, \frac{0}{1}, \frac{0}{-1}, \frac{0}{2}, \frac{-2}{3}\) are rational numbers.

Question 3.
Mention five rational numbers each of whose:
(a) Numerator is a negative integer and denominator is a positive integer.
(b) Numerator is positive integer and denominator is a negative integer.
(c) Numerator and denominator are both negative integers.
(d) Numerator and denominator are both positive integers.
Solution:

Question 4.
Fill in the boxes:

Solution:

Question 5.
Is 5 a positive rational number ?
Solution:
Yes, 5 is a positive rational number.

Question 6.
List five more positive rational number.
Solution:
\(\frac{5}{6}, \frac{-7}{-11}, \frac{5}{7}, \frac{36}{63}, \frac{17}{19}\)

Question 7.
Q. 1. Is – 8 a negative rational number ?
Solution:
Yes, – 8 is a negative rational number.

Question 8.
List five more negative rational number.
Solution:
\(\frac{-16}{6}, \frac{-8}{3}, \frac{-24}{9}, \frac{-32}{12}, \frac{-40}{15}\)

Question 9.
Which of these are negative rational numbers ?
(i) \(\frac{-2}{3}\)
(ii) \(\frac{5}{7}\)
(iii) \(\frac{3}{-5}\)
(iv) 0
(v) \(\frac{6}{11}\)
(vi) \(\frac{-2}{-9}\)
Solution:

Question 10.
Find the standard form of:
(i) \(\frac{-18}{45}\)
(ii) \(\frac{-12}{18}\)
Solution:

Question 11.
Find five rational number between \(\frac{-5}{7}\) and \(\frac{-3}{8}\)
Solution:

Now we have common denominator. Number between – 40 and – 21 are – 39, -38, – 37, – 36, – 35, – 20.
So, we can choose any five out of them.

Question 12.
Find:
(i) \(\frac{-13}{7}+\frac{6}{7}\)
(ii) \(\frac{19}{5}+\frac{-7}{5}\)
Solution:

Question 13.
Find:
(i) \(\frac{3}{7}+\frac{2}{3}\)
(ii) \(\frac{-5}{6}+\frac{-3}{11}\)
Solution:

Question 14.
What is additive inverse?
(i) \(\frac{-3}{9}\)
(ii) \(\frac{-9}{11}\) and
(iii) \(\frac{5}{7}\)
Solution:
(i) \(\frac{-3}{9}=\frac{3}{9}\)
(ii) \(\frac{-9}{11}=\frac{9}{11}\)
(iii) \(\frac{5}{7}=\frac{-5}{7}\)

Question 15.
Find:
(i) \(\frac{7}{5}-\frac{2}{5}\)
(ii) \(2 \frac{1}{5}-\frac{-1}{3}\)
Solution:

Question 16.
What are the multiplication?
(i) \(\frac{-3}{4} \times 7\)
(ii) \(\frac{-6}{5} \times(-2)\)
Solution:

Question 17.
Find:
(i) \(\frac{-3}{4} \times \frac{1}{7}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}\)
Solution:
(i) \(\frac{-3}{4} \times \frac{1}{7}=\frac{-3}{28}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}=\frac{-10}{27}\)

Question 18.
What will be the reciprocal of \(\frac{-6}{11}\)?\(\frac{-8}{5}\)?
Solution:

Question 19.
Find
\(\frac{2}{3} \times \frac{-7}{8}\)
Solution:
\(\frac{2}{3} \times \frac{-7}{8}=\frac{-14}{24}=\frac{-7}{12}\)

Question 20.
Find
\(\frac{-6}{7} \div \frac{5}{7}\)
Solution:
\(\frac{-6}{5} \div \frac{5}{7}=\frac{-6}{5} \times \frac{7}{5}=\frac{-42}{25}\)

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry InText Questions

Think, Discuss & Write (Page No. 195):

Question 1.
In the adjoining construction, can you draw any other line through A that would be also parallel to the line 7 ?
Solution:
Yes, i.e.l || m,
Hence, m || n.

Question 2.
Can you slightly modify the adjoining construction to use the idea of equal correspon¬ding angles instead of equal alternate angles ?

Solution:
From construction and Fig. We have alternate angles and corresponding angles are equal.
Hence line l || m || n.

Think, Discuss & Write (Page No. 198):

Question 1.
A student attempted to draw a triangle whose rough figure is given here. He drew QR first. Then with Q as centre, he drew an arc of 3 cm and with R as centre, he drew an arc of 2 cm. But he could not get P. What is the reason ? What property of triangle do you dnow in connection with this problem ?
Can such a triangle exist ? (Remember the property of triangles. ‘The sum of any two sides of a triangle is always greter than the third side’!)

Solution:
Since, 3 cm + 2 cm = 5 cm < 6 cm 3 cm + 6 cm = 9 cm > 2 cm
2 cm + 6 cm = 8 cm > 3 cm
Hence, 3 cm, 2 cm and 6 cm are not the
sides of any triangle.
Because, “The sum of any two sides of a triangle is always greater than the third side”.

Think, Discuss & Write (Page No. 195):

Question 1.
In the above example, length of a side and measures of two angles were given. Now study the following problem :
In ΔABC, if AC = 7 cm, m∠A = 60° and m∠B = 50°, can you draw the triangle ? (Angle- sum property of a triangle may help you!)

Solution:
Angle sum property, sum of the three angles of a triangle is 180°.
Hence, ∠A + ∠B + ∠C = 180°
or, 60 + 50 + ∠C = 180°
or, ∠C = 180°-110°
∴ ∠C = 70°
Therefore, we can draw the triangle.
In ΔABC, if AC = 7 cm, m∠A = 60°, m∠B = 50°
∴ m∠C = 70°
Then ΔABC is the required triangle.

Miscellaneous Questions (Page No. 195):

Question 1.
Below are given the measures of certain sides and angles of triangles. Identify those which cannot be constructed and say why you cannot construct them. Construct rest of the triangles.
Triangle — Given measurements
1. ΔABC — m∠A = 85°; m∠B -115°; AB = 5 cm.
2. ΔPQR — m∠Q = 30°; m∠R = 60°; QR -4.7 cm.
3. ΔABC — m∠A = 70°; m∠B = 50°; AC = 3 cm.
4. ΔLMN — m∠L = 85° ; m∠N = 115; LM = 5 cm.
5. ΔABC — BC = 2 cm; AB = 4 cm ; AC = 2 cm.
a ΔPQR — PQ = 3.5 cm ; QR = 4 cm ; PR = 3.5 cm.
7. ΔXYZ — XY=3 c m ; YZ = 4 cm ; XZ = 5 cm.
8. ΔDEF — DE = 4.5 cm ; EF = 5.5 cm ; DF = 4 cm.
Solution:
1 In ΔABC, ∠A + ∠B = 85° + 115° = 200° which is not possible as the sum of three angles of a triangle is 180°. So this triangle cannot be constructed.
2. ∠Q + ∠R = 30° + 60° = 90° which is possible so the triangle can be constructed.

Steps of Construction :

1. Draw QR = 4.5 cm.
2. Usin g protractor at Q, draw an ∠Q = 30° and at R draw an ∠R = 60°.
3. Let the two new arms of these angles meet at P.
Thus the required triangle is ΔPQR.
3. ∠A + ∠B = 70° + 50° = 120°
∴ ∠C = 60°
So, this triangle can be constructed.

Steps of Construction :
1. Draw AC = 3cm.
2. At A, draw an
∠A = 70° (using protractor)
At C, draw an ∠C = 60° (using protractor)
3. Let the two arms of the new angles intersect each other at B.
Thus ΔABC is the required triangle.

4. ∠L + ∠N = 85° + 115° = 200° Which is not possible, because the sum of the three angles of a triangle is 180°.
So, such a triangle cannot be constructed.
5. Now BC + CA = 2 + 2 = 4 cm but
AB = 4 cm
∴ BC + CA = AB
But in a triangle, sum of two sides is always greater than the third.
Thus such a triangle cannot be constructed.
6. Now PQ + PR = 3.5 cm + 3.5 = 7 cm and QR = 4 cm.

∴ PQ + PR > QR is true because sum of two sides of a triangle is always greater than the third.
Thus this triangle can be constructed.

Steps of Construction :
1. Draw QR = 4 cm.
2. With Q and R as centre and radii 3.5 cm draw two arcs intersecting each other at P.
3. Join PQ and PR.
Now ΔPQR is the required triangle.
7. Now XY + YZ = 3 + 4 = 7 cm and XZ = 5 cm
∴ XY + YZ > XZ.
In a triangle, the sum of two sides is always greater than the third.
Thus such a triangle can be constructed.

Steps of construction :
1. Draw XZ = 5 cm.
2. With X and Z as centres and respecitve radii as 3 cm and 4 cm, draw two arcs intersecting each other at Y.
3. Join YX and YZ.
Thus, we get the required ΔXYZ.
8. DE + DF = 4.5 + 4 cm = 8.5 cm.
Also EF = 5.5 cm
∴ DE + DF > EF which is true, because sum of two sides of a triangle is greater than the third.
Thus such a Δ can be constructed.
Steps of Construction :
1. Draw DE = 4.5 cm.
2. with D and E as centres and respective radii as 4 cm and 5.5 cm draw two arcs intersecting each other at F.
3. Join DF and EF.
Thus we get the required ΔDEF.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry  Exercise 10.5

Question 1.
Construct the right-angled ΔABC where m∠B = 90°, BC = 8 cm and AC = 10 cm.
Solution:
Steps of construction :
1. Draw a line segment QR = 8 cm.
2. At Q, construct ∠RQX = 90°.
3. With centre at R and radius 10 cm, draw an arc to cut \(\) at P.
4. Join PR.
Thus, ∠PQR is the required right angled triangle.

Question 2.
Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm. Long.
Solution:
Steps of Construction :
1. Draw a line segment MN = 4 cm.
2. Construct ∠NMX = 90° at M.
3. With centre at N and radius 6 cm, draw an arc to cut \(\overline{\mathrm{MX}}\) at L.
4. Join LN.
Thus, ΔLMN is the required right-angled triangle.

Question 3.
Construct an isoscales right¬angled triangle ABC where m∠ACB = 90° and AC = 4 cm.
Solution:
Steps of Construction :
1. Draw a line segment AC = 6 cm.
2. At C, construct, ∠ACX = 90°.
3. With centre C and radius = AC = 6 cm,
draw an arc to cut \(\overline{\mathrm{CX}}\) B.
4. Join BA.
Thus, ΔABC is the required isosceles right, angled triangle.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry  Exercise 10.4

Question 1.
Construct ΔABC, given m∠A = 60°, m∠B = 30° and AB = 5 cm.
Solution:
Draw a rough sketch of ΔABC and indicate the measures of the two angles and length of the included side.
Steps of Construction :
1. Draw a ray BP.
2. From ray BP, cut off a line-segment BA = 5 cm.

3. At M, construct ∠XBA of measure 30°. (Fig.)
4. At A construct ∠YAB of measure 60°. Let the rays BX and AY intersect at C. Then ΔABC is the required triangle. (Fig.)

Question 2.
Construct ΔPQR if PQ = 5 cm, m∠PQR = 105° and m∠QRP = 40°. (Hint : Recall angle-sum property of a triangle).
Solution:
Angle sum property of a triangle
∠P + ∠Q + ∠R = 180°
∠P + 105° + 40° = 180°
or, ∠P = 180°-145°
∴ ∠P = 35°
Steps of Construction :
1. Construct PQ = 5 cm.
2. Using protractor, draw ∠Q = 105° and ∠P = 35°.
3. Let their new arms meet at R. Now ΔPQR is the required triangle.

Question 3.
Examine whether you can construct ΔDEF such that EF = 7.2 cm, m∠E = 110° and m∠F = 80°. Justify your answer.
Solution:
In ΔDEF, EF = 7.2 cm and
∠E + ∠F + ∠D = 180°
But, 110+ 80 +∠D ≠ 180°
or, 190° + ∠D ≠ 180°
Which is not possible as the sum of three angles of a triangle is 180°, So this triangle cannot be constructed.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry  Exercise 10.3

Question 1.
Construct ADEF such that DE = 5 cm., DF = 4 cm and ∠EDF = 90°.
Solution:
Steps of Construction :
1. Draw DE = 5 cm.
2. At D draw ∠FDE = 90°.
3. Along DF, cut off DF = 4 cm.
4. Join E and F.
ΔDEF is the required triangle.

Question 2.
Construct an isosecels triangle in which the length of each of its equal sides is 6.5 cm and the angle between them is 110°.
Solution:
Draw a rough sketch of ΔABC and indicate the lengths of its sides and the measure of the included angle.
Steps Of Construction :
1. Draw a ray BP.
2. From ray BP, cut off a line-segment BC = 6.5 cm. (Fig.)

3. At B, construct ∠QBC = 110°. (Fig.)
4. From ray BQ, cut off a line-segment BA = 6.5 cm. (Fig.)

5. Join AC to obtain the required triangle ABC. (Fig.)

Question 3.
Construct ΔABC with BC = 7.5 cm, AC = 5 cm and m∠C = 60°.
Solution:
Steps of Construction :

1. Draw a line segment BC = 7.5 cm.
2. At C, construct ∠BCX = 60°.
3. From the ray CX, cut off CA = 5 cm.
4. Join AB.
Thus, ABC is the required triangle.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry  Exercise 10.2

Question 1.
Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Solution:
We first draw a rough sketch of AXYZ and indicate the lengths of its sides.

Steps of Construction :
1. Draw a line segment ZX of length 6 cm.
2. With centre Z and radius 5 cm, draw an arc of the circle.
3. With centre X and radius 4.5 cm draw another arc intersecting the arc draw in step 2 at Y.
4. Join ZY and XY to obtain the desired triangle.
Since no two sides of the triangle are equal so it is a scalene triangle.

Question 2.
Construct an equilateral triangle of side 5.5 cm.
Solution:

Steps of Construction :
1. Draw a line segment BC = 5.5 cm.
2. With B as centre and radius 5.5 cm, draw an arc.
3. With centre C and radius 5.5 cm, draw another arc to cut the previous arc at A.
4. Join BA and CA.
Thus, ΔABC is the required equilateral triangle.

Question 3.
Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this ?
Solution:

Step of Construction
1. Construct PQ = 4 cm.
2. With P as centre and radius 4 cm draw an arc.
3. With Q as centre and radius 3.5 cm draw another arc, intersecting the previous arc at R.
4. Join PR and QR.
Now ΔPQR is the required triangle.

Question 4.
Construct ΔABC such that AB = 2.5 cm, BC = 6 cm an AC = 6.5 cm. Measure ZB.
Solution:

Steps of Construction :
1. First, we draw a rough sketch with give n, measure, (this will help us in deciding how to proceed).
2. Draw a line segment BC of length 6 cm.
3. From B, point A is at a distance of 2.5 cm. So, with B as centre, draw an arc of radius 2.5 cm. (Now will be somewhere on this arc. Our job is to find where exactly A is).
4. From C, point A is at a distance of 6.5 cm. So, with C as centre, draw an arc of radius 6.5 cm. (A will be somewhere on this arc we have to fix it).
5. A has to be on both the arcs drawn. So it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC. AABC is now ready.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry  Exercise 10.1

Question 1.
Draw a line, say AB, take a point C outside it. Through C, draw using ruler and compasses only, a line parallel to AB.
Solution:
Step :
1. Take a line AB and a point ‘C’ outside ‘AB’.
2. Take any point ‘D’ on line AB and join D to C.


3. With D as centre and a convenient radius, draw an arc cutting 1 at E and DC at F.
4. Now with C as centre and the same radius as in step 3, draw an arc GH cutting CD at K.
5. Place the pointed tip of the compasses at E and adjust the opening so that the pencil tip is at F.
6. With the same opening as in step 5 and with K as centre, draw an arc cutting the arc GH at L.
7. Now join CL to draw a line PQ.
Hence, ∠1 = ∠2 = alternate interior angles.

Question 2.
Draw a line l. Draw a perpendicular to l at any point on l. On this perpendicular choose a point X that is 4 cm away from l. Through X draw a line m parallel to l.
Solution:
Step :
1. Take a line l
2. Take any point B on l,
3. Take a point X out side l and perpendicular 4 cm away from line T.
4. Through X draw a line m. i.e. l \\m
i.e., ∠1 = ∠2 = 90° = alternate angles
Hence line l || line m.

Question 3.
Let ∠ be a line and P be point not on ∠. Through P draw a line m parallel to P. Now join P to any point Q or l. Choose any other point R on m, Through R draw a line parallel to PQ.
Let this meet l at S. What shape do the two sets of parallel lines enclose ?

Solution:
Step :
1. Take a line T.
2. Take a point P out side of T.
3. Through P draw a line m parallel to P at any point Q or l.
4. Draw R on m and parallel to PQ.
5. Line m R meet at point on line l.
Hence, we say, line l is transversal of P || m.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 9 Rational Numbers Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 9 Rational Numbers Exercise 9.1

Question 1.
List five rational number between :
(i) – 1 and 0 (ii) – 2 and – 1
(iii) \(\frac{-4}{5}\) and \(\frac{-2}{3}\)
(iv) \(\frac{1}{2}\) and \(\frac{2}{3}\)
Solution:
(i) Let us write – 1 and 0 as rational number with denominator 6.
We have, – 1 = \(\frac{-6}{6}\), 0 = \(\frac{0}{6}\)

(ii) Let us write -2 and -1 as rational number with denominator 6.

Question 2.
Write four more rational number in each of the following patterns:

Solution:

Question 3.
Give four rational numbers equivalent to —
(i) \(\frac{-2}{7}\)
(ii) \(\frac{5}{-3}\)
(iii) \(\frac{4}{9}\)
Solution:

Question 4.
Draw the number line and represent the following rational number on it:
(i) \(\frac{3}{4}\)
(ii) \(\frac{-5}{8}\)
(iii) \(\frac{-7}{4}\)
(iv) \(\frac{7}{8}\)
Solution:
(i) \(\frac{3}{4}\) Let us represent the rational number \(\frac{3}{4}\) on the number line.

(ii) \(\frac{-5}{8}\). Let us represent the rational number \(\frac{-5}{8}\) on the number line.

(iii) \(\frac{-7}{4}\). Let us represent the rational number \(\frac{-7}{4}\) on the number line.

(iv) \(\frac{7}{8}\). Let us represent the rational number \(\frac{7}{8}\) on the number line.

Question 5.
The point P, Q, R, S, T, U, A and B on the number line are such that TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.

Solution:
The point P, Q, R, S on this number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R, S.
Now,

Question 6.
Which of the following pairs represent the same rational number?

Solution:
\(\frac{-7}{21} \text { and } \frac{3}{9}\)
We multiply the numerator and denominator of the first number by the denominator of the second, we have,
\(\frac{-7}{21}=\frac{-7 \times 9}{21 \times 9}=\frac{-63}{189}\)
Again we multiply the numerator and denominator of the second number by the denominator of the first, we have,

(ii) \(\frac{-16}{20} \text { and } \frac{20}{25}\)
We multiply the numerator and denominator of the first number by the denominator of the second, we have,
\(\frac{-16 \times 25}{20 \times 25}=\frac{-400}{500}\)

Again we multiply the numerator and denominator of the second number by the denominator of the first, we have,

(iv) \(\frac{-3}{5} \text { and } \frac{-12}{20}\)
We multiply the numerator and denominator of the first number by the denominator of second, we have -2 -2×3 -6
\(\frac{-3}{5}=\frac{-3 \times 20}{5 \times 20}=\frac{-60}{100}\)
Again we multiply the numerator and denominator of the second number by the denominator of the first, we have

(v) \(\frac{8}{-5} \text { and } \frac{-24}{15}\)
We multiply the numerator and denominator of the first number by the denominator of second, we have,
\(\frac{8}{-5}=\frac{8 \times 15}{-5 \times 15}=\frac{120}{-75}\)
Again we multiply the numerator and denominator of the second number by the denominator of the first, we have,

(vi) \(\frac{1}{3} \text { and } \frac{-1}{9}\)
We multiply the numerator and denominator of the first number by the denominator of the second, we have,
\(\frac{1}{3}=\frac{1 \times 9}{3 \times 9}=\frac{9}{27}\)
Again we multiply the numerator and denominator of the second number by the denominator of the first, we have,

(vii) \(\frac{-5}{-9} \text { and } \frac{5}{-9}\)
We multiply the numerator and denominator of the first number by the denominator of the second, we have,
\(\frac{-5}{-9}=\frac{-5 \times-9}{-9 \times-9}=\frac{45}{81}\)
Again we multiply the numerator and denominator of the second number by the denominator of the first, we have,

Question 7.
Rewrite the following rational number in the simplest form :
(i) \(\frac{-8}{6}\)
(ii) \(\frac{25}{45}\)
(iii) \(\frac{-44}{72}\)
(iv) \(\frac{-8}{10}\)
Solution:

Question 7.
Fill in the boxes with the correct symbol out of >,<. and =.

Solution:

Question 9.
Which is the greater in each of the following:

Solution:

Question 10.
Write the following rational numbers in ascending order:

Solution:

Haryana State Board HBSE 7th Class Maths Solutions Chapter 9 Rational Numbers Ex 9.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 9 Rational Numbers Exercise 9.2

Question 1.
Find the sum :

Solution:

Question 2.
Find

Solution:

Question 3.
Find the product:

Solution:

Question 4.
Find the value of:

Solution:

Haryana State Board HBSE 7th Class Maths Solutions Chapter 8 Comparing Quantities InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 8 Comparing Quantities InText Questions

Question 1.
An ant can carry 50 times its weight. If a person can do the same, how much would you carry ?
Solution:
If an ant carry 50 times its weight. Then, a person carry 50 times its weight.
If a person of weight = 50 kg.
Then, a person carry 50 x 50 = 2500 kg.

Question 2.
Find the percentage of children of different heights for the following data:

Solution:

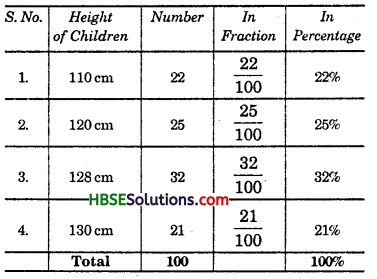
Question 3.
A shop has the following number of shoe pairs of different sizes:
Size 2 20
Size 3 30
Size 4 28
Size 5 14
Size 6 8
Write this informal in tabular form as done earlier and find the percentage of each shoe size available.
Solution:

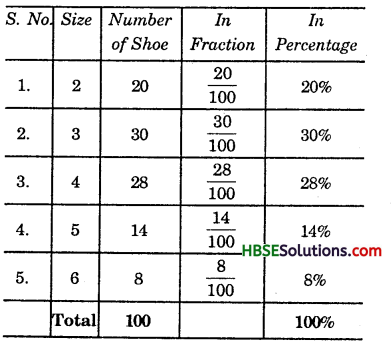
Question 4.
A collection of 10 chips is with different colours is given.

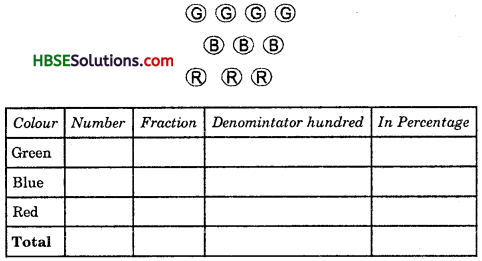
Fill the table and find the percentage of chips of chips of each colour?
Solution:

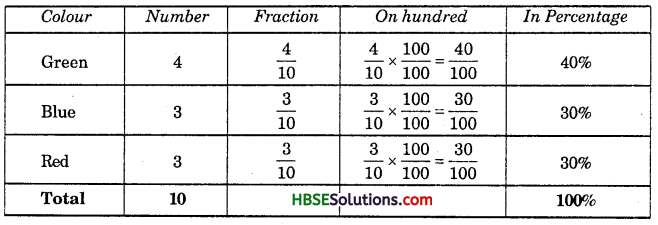
Question 5.
Mala has a collection of bangles. She has 20 gold bangles and 10 silver bangles. What is the percentage of bangles of each type ? Can you put it in the tabular form as done in the above example ?
We have seen that percentages also can be used for comparing quantities.
Solution:

Question 6.
Look at the examples below and in each of them, discuss which is better for comparison.
Solution:
In the atmosphere, 1 g of air contains :
.78 g Nitrogen
.21 g Oxygen
.01 g Other gas
Solution:
1 g of air = 0.78g + 0.21g + 0.01g = 1.00g
or, 100% of air = 78% + 21% + 1% = 100%
or,0.78 g Nitrogen = \(\frac{0.78}{100}=\frac{78}{100}\) =78%
0.21 g Oxygen = \(\frac{0.21}{100}=\frac{21}{100}\) = 21%
0.01 g Other gas = \(\frac{0.01}{100}=\frac{1}{100}\) = 1%

Question 7.
A shirt has :
3/5 Cotton or 60% Cotton
2/5 Polyster 40% Polyster
Solution:

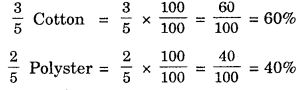
Question 8.
(i) Can you eat 50% of a cake ?
Can you eat 100% of a cake ?
Can you eat 150% of a cake ?
(ii) Can a price of an item go up by 50% Can a price of an item go up by 100% Can a price of an item go up by 150%
Solution:
(i) Yes, Yes, No.
(ii) Yes, Yes, Yes.

Question 9.
Convert the following to percents :
(a) \(\frac{12}{16}\)
(b) 3.5
(c) \(\frac{49}{50}\)
(d) \(\frac{2}{2}\)
(e) 0.05
Solution:

Question 10.
(i) Out of 32 students, 8 are absent. What per cent of the students are absent ?
(ii) There are 25 radios, 16 of them are out of order. What percent radio are out of order?
(iii) A shop has 500 parts, out of which 5 are defective. What percent are defective ?
(iv) There are 120 voters, 90 of them voted yes. What percent voted yes ?
Solution:
(i) Percentage of absent = \(\frac{8}{32}\) x 100% = 25%
(ii) Percentage of out of order \(\frac{16}{25}\) x 100% = 64%
(iii) Percentage of defective = \(\frac{5}{500}\) x 100% = 1%
(iv) Percentage of yes = \(\frac{90}{120}\) x 100% = 75%.

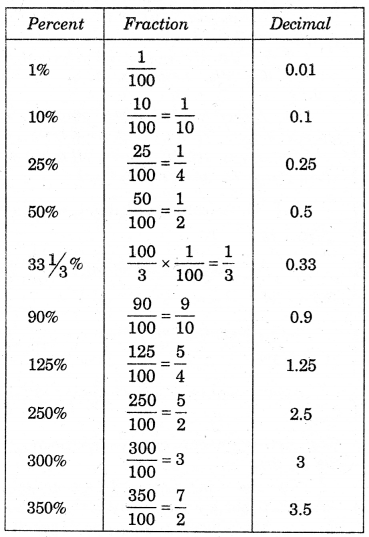
Question 11.
Converting percentages to fractions or decimals :
We have so far converted fractions and decimals to percentages. We can also do the inverse that is when given percentages we can convert it to decimals or fractions. Look at the table, observe and complete it:

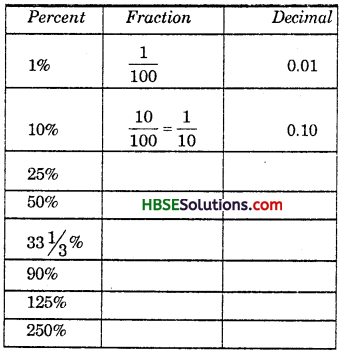
Make some more such examples and solve them.
Solution:

Question 12.
35% + ………….% = 100%
64% + 20% + ………….% = 100%
45% = 100%- ………….%
70% =…………. % – 30%
Solution:
(100-35)% = 65%
[100-(64+ 20)]% = (100-84)%
= 16%
(100-45)% = 55%
(70 + 30)% = 100%

Question 13.
If 65% of students in a class have a bicycle, what percent of the student do not have bicycles
Solution:
Percentage of not have cycles
= (100-65)%
= 35%

Question 14.
We have a basket full of apples, oranges and mangoes. If 50% are apples, 30% are oranges, then what percent are mangoes ?

Solution:
Percentage of mangoes
= [100-(50+ 30)]%
= (100-80)% = 20%

Question 15.
Consider the expenditure made on a dress 20% on embroidery, 50% on cloth, 30% on stitching. Can you thind of more such examples ?
Solution:
Yes; consider the expenditure made on a building.
20% on labours, 50% on bricks, 30% on cement and etc.

Question 16.
What per cent of these figures are sheded. You can now make some figures yourself and ask your friends to estimate the shaded parts.

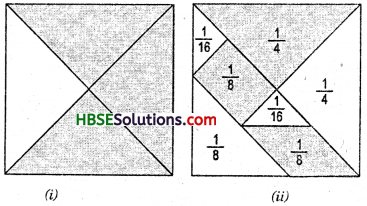
(i) Percentage of shaded parts 75

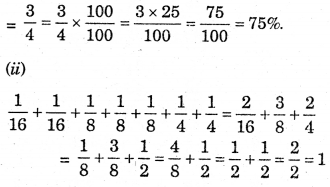
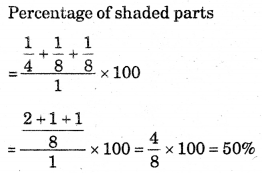
Question 17.
Find (a) 50% of 164
(b) 75% of 12
(c) 12 1/2 % of 64
Solution:
(a) 50% of 164 = \(\frac{50}{100}\) x 164 = 82
(b) 75% of 12 = \(\frac{75}{100}\) x 12 = 9
(c) 12 1/2 % of 64 = \(\frac{25}{2} \times \frac{1}{100}\) x 64 = 8

Question 18.
8% children of a class of 25 like getting wet in rains. How many children like getting wet in rains ?
Solution:
8% of 25 = \(\frac{8}{100}\) x 25 = 2
Hence, 2 children like getting wet in rains.

Question 19.
9 is 25% of what number ?
Solution:
25% of x = 9
\(\frac{25}{100}\) x x = 9
\(\frac{x}{4}=\frac{9}{1}\)
Hence no. x = 4 x 9 = 36.

Question 20.
75% of what number is 15 ?
Solution:
Let be no. be x.
75% of x = 15
\(\frac{75}{100}\) x x = 15
\(\frac{3x}{4}\) = 15 3x = 15 x 4
x = \(\frac{15 \times 4}{3}\) = 20

Question 21.
Divide 15 sweets between Manu and Sonu so that they get 20% and 80% of them respectively.
Solution:
Manu gets,
20% of 15 sweets = \(\frac{75}{100}\) x 15 = 3 sweets Sonu gets,
80% of 15 sweets = \(\frac{75}{100}\) x 15 = 12 sweets

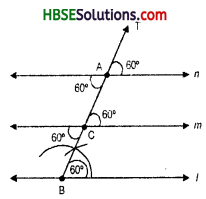
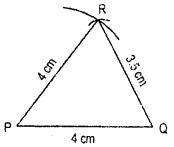
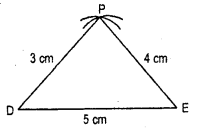
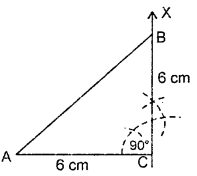
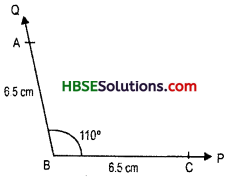
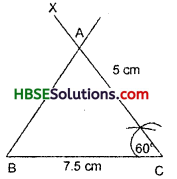
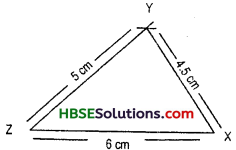
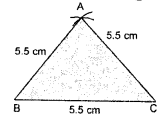
Question 22.
If angles of a triangle are in ratio 2:3:4. Find one value of each angle.
Solution:
The sum of angles of a triangle
Let x be an angle = 180°
Hence, 2x + 3x + 4x = 180°
or, 9x = 180°
or x = \(\frac{180°}{9}\)
or, x = 20 = one value of each angle.
i.e., 40°, 60°, 80° are the three angles of a triangle.

Question 23.
Find percentage of increase or decrease.
(i) Price of shirt decreased from Rs. 80 to Rs. 60.
(ii) Marks in a test in creased from 20 to 30.
Solution:
Percent increase or decrease

Question 24.
My mother says, in her childhood petrol was Rs. 1 a litre. It is Rs. 52 per litre today. By what percentage gas the price gone up ?
Solution:
Original rate of one litre petrol = Rs.1
The increase in rate of one litre petrol
= Rs. 52 – Rs. 1 = Rs. 51
∴ Percentage increase
Amount of change = \(\frac{Amount of change}
{Original amount}\) x 100%
= \(\frac{51}{1}\) x 100 = 5100%
Hence, 5100% has price gone up.

Question 25.
A shopkeeper bought a chair for Rs. 375 and sold it for Rs. 400. Find the gain percentage.
Solution:
C.P. = Rs. 375, S.P. = Rs. 400
Gain = S.P. – C.P. = 400 – 375
= Rs. 25.
∴ Gain % = \(\frac{\text { Gain }}{\text { C.P. }}\) x 100%
\(\frac{25}{375} \times 100=\frac{20}{3}=6 \frac{2}{3} \%\)

Question 26.
Cost of an item is Rs. 50; It was sold with a profit of 12%. Find the selling price.
Solution:
C.P. = Rs. 50, S.P. = ?
Gain % = 12%

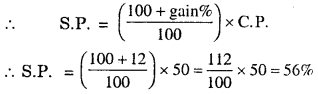
Question 27.
An article was sold for Rs. 250 with a profit of 5%, then what is the cost price ?
Solution:
C.P = ?
S.P. = Rs. 250, Gain% = 5%

Question 28.
An item sold for Rs. 540 at a loss of 5%. What was its cost price ?
Solution:
S.P. = Rs. 540, C.P. = ?
loss% = 5%

Question 29.
Rs. 10,000 is invested at 5% interest rate p.a. Find the interest at end of one year.
Solution:
Here, P = Rs. 10,000, R = 15%,
T = 1 year
∵ S.I = \(\frac{\mathrm{PRT}}{100}\)
∴ S.I = \(\frac{10,000 \times 15 \times 1}{100}\) = Rs. 1,500

Question 30.
Rs. 3500 is given at 7% p.a. rate of interest. Find the interest which will be received at end of two years.
Solution:
P = Rs. 3500, R = 7%, T = 1 year
∴ S.I = \(\frac{3,500 \times 7 \times 1}{100}\) = Rs. 245

Question 31.
Rs. 6050 is borrowed at 6.5% rate of interest p.a. Find the interest and the amount to be paid at the end of 3 years.
Solution:
P. = Rs. 6050,
R = 6.5%, T = 3 years
S.I = \(\frac{6,050 \times 6.5 \times 3}{100}\) = Rs. 395.25 100
P + I = 6050 + 395.25
.’. Amount = Rs. 6445.25

Question 32.
Rs. 7000 is borrowed at 3.5% rate of interest p.a. borrowed for 2 years. Find the amount to be paid at end of second year. Solution:
P = Rs. 7,000, R = 3.5%,
T = 2 years.
S.I = \(\frac{7,000 \times 3.5 \times 2}{100}\) = Rs 280
A = P + I
Amount = 7000 + 280 = Rs. 7280.

Question 33.
If you had Rs. 2400 in your account and the interest rate were 5%. After how many years would you earn Rs. 240 as interest ?
Solution:
P = Rs. 2400, R = 5%, T = ?
S.I. = Rs. 240
S.I = \(\frac{\text { PRT }}{100}\)
T = \(\frac{\text { S.I. } \times 100}{\mathrm{PR}}\)
T = \(\frac{2400 \times 100}{2400 \times 5}\) = 2 years

Question 34.
If on a certain sum the interest paid after 3 years is Rs. 450 at 5% rate of interest per annum. Find the sum.
Solution:
Here, P = ? R = 5%, T = 3 years
= Rs. 450
∵ S.I = \(\frac{\text { PRT }}{100}\)
∴ P = \(\frac{\text { S.I. } \times 100}{\mathrm{RT}}\)
∴ P = \(\frac{450 \times 100}{5 \times 3}\)
∴ The sum = Rs. 3000.
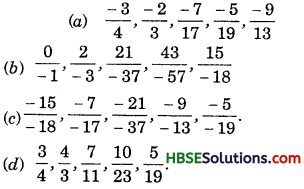
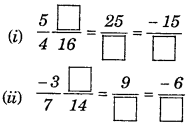
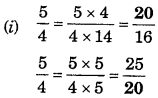
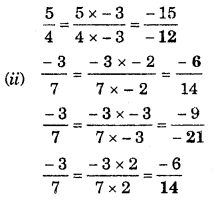
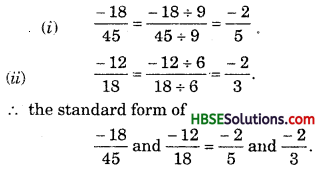
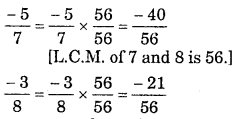
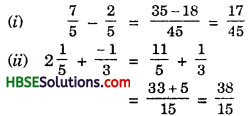
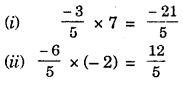