Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry Exercise 10.2
Question 1.
Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Solution:
We first draw a rough sketch of AXYZ and indicate the lengths of its sides.
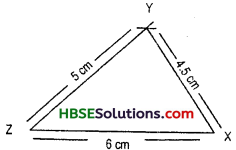
Steps of Construction :
1. Draw a line segment ZX of length 6 cm.
2. With centre Z and radius 5 cm, draw an arc of the circle.
3. With centre X and radius 4.5 cm draw another arc intersecting the arc draw in step 2 at Y.
4. Join ZY and XY to obtain the desired triangle.
Since no two sides of the triangle are equal so it is a scalene triangle.
![]()
Question 2.
Construct an equilateral triangle of side 5.5 cm.
Solution:
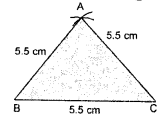
Steps of Construction :
1. Draw a line segment BC = 5.5 cm.
2. With B as centre and radius 5.5 cm, draw an arc.
3. With centre C and radius 5.5 cm, draw another arc to cut the previous arc at A.
4. Join BA and CA.
Thus, ΔABC is the required equilateral triangle.
Question 3.
Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this ?
Solution:
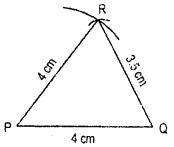
Step of Construction
1. Construct PQ = 4 cm.
2. With P as centre and radius 4 cm draw an arc.
3. With Q as centre and radius 3.5 cm draw another arc, intersecting the previous arc at R.
4. Join PR and QR.
Now ΔPQR is the required triangle.
![]()
Question 4.
Construct ΔABC such that AB = 2.5 cm, BC = 6 cm an AC = 6.5 cm. Measure ZB.
Solution:
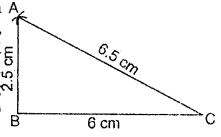
Steps of Construction :
1. First, we draw a rough sketch with give n, measure, (this will help us in deciding how to proceed).
2. Draw a line segment BC of length 6 cm.
3. From B, point A is at a distance of 2.5 cm. So, with B as centre, draw an arc of radius 2.5 cm. (Now will be somewhere on this arc. Our job is to find where exactly A is).
4. From C, point A is at a distance of 6.5 cm. So, with C as centre, draw an arc of radius 6.5 cm. (A will be somewhere on this arc we have to fix it).
5. A has to be on both the arcs drawn. So it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC. AABC is now ready.