Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 Practical Geometry InText Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 10 Practical Geometry InText Questions
Think, Discuss & Write (Page No. 195):
Question 1.
In the adjoining construction, can you draw any other line through A that would be also parallel to the line 7 ?
Solution:
Yes, i.e.l || m,
Hence, m || n.
Question 2.
Can you slightly modify the adjoining construction to use the idea of equal correspon¬ding angles instead of equal alternate angles ?
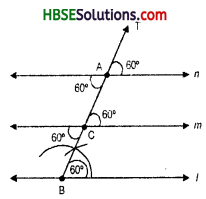
Solution:
From construction and Fig. We have alternate angles and corresponding angles are equal.
Hence line l || m || n.
![]()
Think, Discuss & Write (Page No. 198):
Question 1.
A student attempted to draw a triangle whose rough figure is given here. He drew QR first. Then with Q as centre, he drew an arc of 3 cm and with R as centre, he drew an arc of 2 cm. But he could not get P. What is the reason ? What property of triangle do you dnow in connection with this problem ?
Can such a triangle exist ? (Remember the property of triangles. ‘The sum of any two sides of a triangle is always greter than the third side’!)
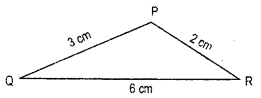
Solution:
Since, 3 cm + 2 cm = 5 cm < 6 cm 3 cm + 6 cm = 9 cm > 2 cm
2 cm + 6 cm = 8 cm > 3 cm
Hence, 3 cm, 2 cm and 6 cm are not the
sides of any triangle.
Because, “The sum of any two sides of a triangle is always greater than the third side”.
Think, Discuss & Write (Page No. 195):
Question 1.
In the above example, length of a side and measures of two angles were given. Now study the following problem :
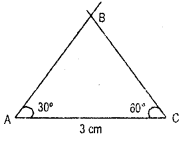
In ΔABC, if AC = 7 cm, m∠A = 60° and m∠B = 50°, can you draw the triangle ? (Angle- sum property of a triangle may help you!)
Solution:
Angle sum property, sum of the three angles of a triangle is 180°.
Hence, ∠A + ∠B + ∠C = 180°
or, 60 + 50 + ∠C = 180°
or, ∠C = 180°-110°
∴ ∠C = 70°
Therefore, we can draw the triangle.
In ΔABC, if AC = 7 cm, m∠A = 60°, m∠B = 50°
∴ m∠C = 70°
Then ΔABC is the required triangle.
![]()
Miscellaneous Questions (Page No. 195):
Question 1.
Below are given the measures of certain sides and angles of triangles. Identify those which cannot be constructed and say why you cannot construct them. Construct rest of the triangles.
Triangle — Given measurements
1. ΔABC — m∠A = 85°; m∠B -115°; AB = 5 cm.
2. ΔPQR — m∠Q = 30°; m∠R = 60°; QR -4.7 cm.
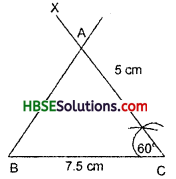
3. ΔABC — m∠A = 70°; m∠B = 50°; AC = 3 cm.
4. ΔLMN — m∠L = 85° ; m∠N = 115; LM = 5 cm.
5. ΔABC — BC = 2 cm; AB = 4 cm ; AC = 2 cm.
a ΔPQR — PQ = 3.5 cm ; QR = 4 cm ; PR = 3.5 cm.
7. ΔXYZ — XY=3 c m ; YZ = 4 cm ; XZ = 5 cm.
8. ΔDEF — DE = 4.5 cm ; EF = 5.5 cm ; DF = 4 cm.
Solution:
1 In ΔABC, ∠A + ∠B = 85° + 115° = 200° which is not possible as the sum of three angles of a triangle is 180°. So this triangle cannot be constructed.
2. ∠Q + ∠R = 30° + 60° = 90° which is possible so the triangle can be constructed.
Steps of Construction :
1. Draw QR = 4.5 cm.
2. Usin g protractor at Q, draw an ∠Q = 30° and at R draw an ∠R = 60°.
3. Let the two new arms of these angles meet at P.
Thus the required triangle is ΔPQR.
3. ∠A + ∠B = 70° + 50° = 120°
∴ ∠C = 60°
So, this triangle can be constructed.

Steps of Construction :
1. Draw AC = 3cm.
2. At A, draw an
∠A = 70° (using protractor)
At C, draw an ∠C = 60° (using protractor)
3. Let the two arms of the new angles intersect each other at B.
Thus ΔABC is the required triangle.
4. ∠L + ∠N = 85° + 115° = 200° Which is not possible, because the sum of the three angles of a triangle is 180°.
So, such a triangle cannot be constructed.
5. Now BC + CA = 2 + 2 = 4 cm but
AB = 4 cm
∴ BC + CA = AB
But in a triangle, sum of two sides is always greater than the third.
Thus such a triangle cannot be constructed.
6. Now PQ + PR = 3.5 cm + 3.5 = 7 cm and QR = 4 cm.
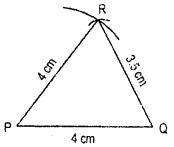
∴ PQ + PR > QR is true because sum of two sides of a triangle is always greater than the third.
Thus this triangle can be constructed.
Steps of Construction :
1. Draw QR = 4 cm.
2. With Q and R as centre and radii 3.5 cm draw two arcs intersecting each other at P.
3. Join PQ and PR.
Now ΔPQR is the required triangle.
7. Now XY + YZ = 3 + 4 = 7 cm and XZ = 5 cm
∴ XY + YZ > XZ.
In a triangle, the sum of two sides is always greater than the third.
Thus such a triangle can be constructed.
Steps of construction :
1. Draw XZ = 5 cm.
2. With X and Z as centres and respecitve radii as 3 cm and 4 cm, draw two arcs intersecting each other at Y.
3. Join YX and YZ.
Thus, we get the required ΔXYZ.
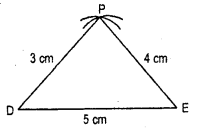
8. DE + DF = 4.5 + 4 cm = 8.5 cm.
Also EF = 5.5 cm
∴ DE + DF > EF which is true, because sum of two sides of a triangle is greater than the third.
Thus such a Δ can be constructed.
Steps of Construction :
1. Draw DE = 4.5 cm.
2. with D and E as centres and respective radii as 4 cm and 5.5 cm draw two arcs intersecting each other at F.
3. Join DF and EF.
Thus we get the required ΔDEF.
![]()