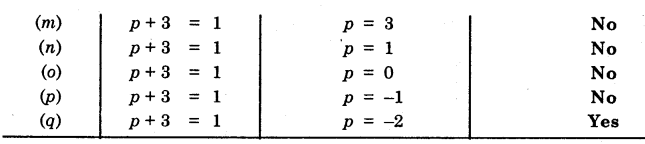Author name: Prasanna

Haryana State Board HBSE 6th Class Maths Solutions Chapter 11 Algebra Ex 11.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 11 Algebra Exercise 11.4

Question 1.
Answer the following :
(а) Take Sarita’s present age to be y years:
(i) What will be her age 5 years from now ?
iii) What was her age 3years back? (lit) Sarita’s grandfather’s age is 6
times her age. What is grand-father’s age ?
(iv) Grandmother is 2 years younger than grandfather. What is grandmother’s age?
(iv) Sarita’s father’s age is 5years more than 3 times Sarita’s age. What is her father’s age ?
(b) The length of a rectangular hall is 4 meters less than 3 times the breadth of the hall. What is the length if the breadth is ‘6’ metres?
(c) A rectangular box has a height ‘h’ cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.
(d) Meena, Beena and Leena are climbing the steps to the hill top. Meena is at step ‘s’, Beena is 8 steps ahead and Leena 7 steps behind. Where are Beena and Leena ? The total number of steps to the hill top is 10 less than 4 times what Meena has reached. Express the total number of steps using ‘s’.
(e) A bus travels at V km per hour. It is going from Daspur to Beespur. After the bus has travelled 5 hours, Beespur is still 20 km away. What is the distance from Daspur to Beespur ? Express it using v.
Solution:
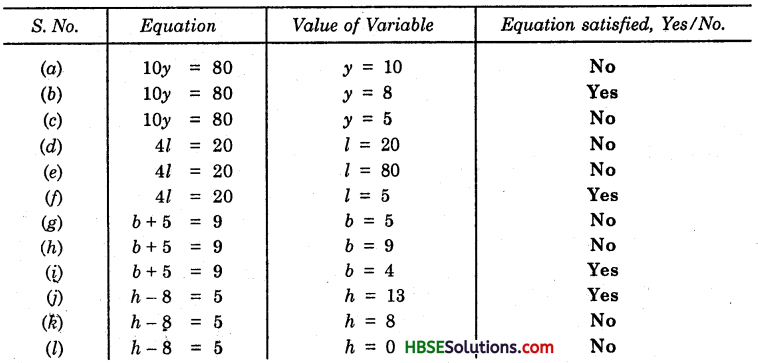
(a) Present age of Sarita = y years.
(i) Her age 5 years from now = (y + 5) years
(ii) Her age 3 years back – (y – 3) years
(iii) Her grandfather’s age = 6y years
(iv) Her grandmother’s age = (6y – 2) years
(v) Her father’s age = (3y + 5) years

(b) Breadth of the hall = b metres
Length of the hall = (3b – 4) metres

(c) Height of the box = h cm
Length of the box = 5h cm
Breadth of the box = (5h – 10) cm

(d) Meena is at step = s
∵ Beena is 8 steps ahead
∴ Beena is at steps =. s + 8.
∵ Leena is 7 steps behind
∴ Leena is at steps = s – 7
Total number of steps = 4s – 10

(e) Speed of the bus = v km per hour
∴ Distance covered in 5 hours = 5 v km.
Hence, distance from Daspur to Beespur = (5 v + 20) km.

Question 2.
Change the following statements into statements in ordinary language.
(For example, Given Salim scores r runs in a cricket match. Nalin scores (r + 15) runs. In ordinary language, Nalin scores 15 runs more than Salim.)
(a) A notebook costs Rs. ‘p’. A book costs Rs. 3p.
(b) Tony puts ‘q’ marbles on the table. He has 8q marbles in his box.
(c) Our class has ‘n’ students. The school has 20 n students.
(d) Jaggu is ‘z’ years old. His uncle is 4z years old and his aunt is (4z- 3) years old.
(e) In an array of dots, there are Y rows. Each row contains 5r dots.
Solution:
(a) A book costs t hree times the cost of a notebook.
(b) Tony’s box contains 8 times the marbles on the table.
(c) Total number of students in the school is 20 times that of our class.
(d) Jaggu’s uncle is 4 times older than Jaggu and his aunt is 3 years younger than his uncle.
(e) The number of dots in a row is 5 times the number of row.

Question 3.
(a) Given, Munnu’s age to be x years. Can you guess what (x – 2) may show ?
[Hint : Think of Munnu’s younger brother.]
Can you guess what (x + 4) may show ? What (3x + 7) may show ?
(b) Given Sara’s age today to be y years. Think of her age in the future or in past. What will the following expression indicate ?
y+1, y-3, y + 4\(\frac{1}{2}\), y-2\(\frac{1}{2}\)
(c) Given, n students in the class like football, what may 2n show ? What may \(\frac{n}{2}\) show ?
[Hint : Think of games other than football.]
Solution:
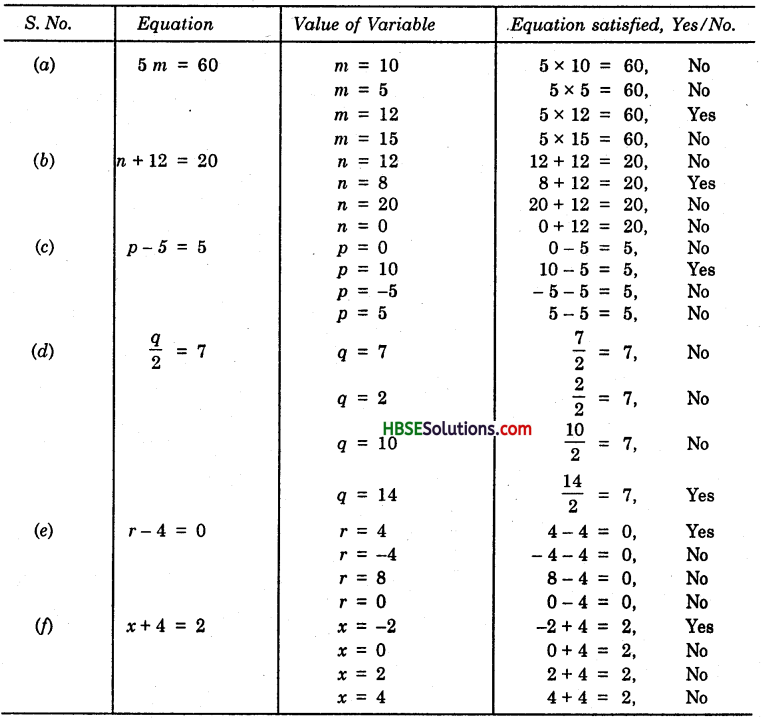
(a) Munnu’s younger brother’s age is 2 years less than Munnu’s age.
His elder sister’s age is 4 years more than his age.
His father’s age is 7 years more than thrice his age.
(b) y + 7 shows her age after 7 years.
y – 3 shows her age 3 years back.
y + 4\(\frac{1}{2}\) shows her age after 4\(\frac{1}{2}\) years.
y – 2\(\frac{1}{2}\) shows her age 2\(\frac{1}{2}\) years back.
(c) n students in the class like football.
2n shows that twice the students in the class like cricket.
\(\frac{n}{2}\) shows that half the students in the class like hockey.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 11 Algebra Ex 11.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 11 Algebra Exercise 11.5

Question 1.
State whether the following are equations or not. Give reason for your answer. Further identify which are equations with only numbers and which are equations with variables. Identify the variables from the equations with variables. Give reason for your answer.
(a) 17 = x+7
(b) (t-7) > 5
(c) \(\frac{4}{2}\) = 8
(ci) 7 x 3 – 19 = 8
(e) 5 x 4 – 8 = 2x
(f) x-2 = 0
(g) 2m < 30
(h) 2n+11 = 1
(j) 7 = 11 x 5 – 12 x 4
(j) 7 = 11 x 2 + p
(k) 20= 5y
(l) \(\frac{3 q}{2}\)< 5 (m) z + 12 > 24
(n) 20- (10-5) = 3×5
(o) 7 – x = 5.
Solution:
(6) It is not an equation because there is no sign of (=).
(c) It is an equation with numbers only.
(d) It is an equation with numbers only
(e) It is an equation with variable ‘r’
(f) It is an equation with variable ‘x’.
(g) It is not an equation because there is no sign of (=).
(h) It is an equation with variable ‘n’
(i) It is an equation with numbers only
(j) It is an equation with variable ‘p’
(k) It is an equation with variable ‘y’
(l) It is not an equation because there is no sign of (=).
(m) It is not an equation because there is no sign of (=).
(n) It is an equation with numbers only
(o) It is an equation with variable ‘x’.

Question 2.
Complete the entries in the third column of the table :
Solution:

Question 3.
Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation. .
(a) 5m- 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (O, 10, 5, -5)
(d) \(\frac{q}{2}\) = 7 (7, 2, 10, 14)
(e) r – 4 = 0 (4, -4, 8, 0).
(f) x + 4 = 2 (-2, 0, 2, 4)
Solution:

Question 4.
(a) Complete the table and by inspection of the table, find the solution to the equation m + 10 = 16
Solution:

m = 6 is the solution of the equation m + 10 = 16.

(b) Complete the table and by inspection of the table find the solution to the equation 5t = 35

Solution:
t = 7 is the solution of the equation 5t = 35.

(c) Complete the table and find the table the solution of the equation \(\frac{z}{3}\) = 4

z – 12 is the solution of the equation \(\frac{z}{3}\) = 4.

(d) Complete the table and find the solution to the equation m – 7 = 3

m = 10 is the solution of the equation m – 7 = 3.

Question 5.
Solve:
(a) x + 5 = 12
(b) y – 2 = 10
(c) 7p = 210
(d) \(\frac{q}{2}\) = 5
(e) t + 100 = 125
(f) l – 20 = 30
(g) 9u = 81
(h) \(\frac{k}{8}\) = 20
(i) 3y = 33
(j) x-3 = 0
(k) \(\frac{k}{8}\) = 8
(l) 13y = 65
Solution:
(a) x + 5 = 12
x = 12 – 5 = 7
Thus, x = 7 is the required solution of the given equation.

(b) y- 2 = 10
⇒ y = 10 + 2 = 12
Thus, y = 12 is the required solution of the given equation.

(c) 7p = 210
⇒ P = \(\frac{210}{7}\) = 30
Thus, p = 30 is the required solution of the given equation.

(d) \(\frac{q}{2}\) = 5
⇒ q = 2 x 5 = 10
Thus, q = 10 is the required solution of the given equation.

(e) t + 100 = 125
⇒ t = 125 – 100 = 25
Thus, t = 25 is the required solution of the given equation.

(f) 1 – 20 = 30
⇒ l = 30 + 20 = 50
Thus, 1 = 50 is the required solution of the given equation.

(g) 9 u = 81
⇒ u = \(\frac{81}{9}\) = 9
Thus, u = 9 is the required solution of the given equation.

(h) \(\frac{k}{8}\) = 20
⇒ k = 8 x 20= 160
Thus, ft = 160 is the required solution of the given equation.

(i) 3y = 33
⇒ y = \(\frac{33}{3}\) = 11
Thus, y = 11 is the required solution of the given equation.

(j) x- 3 = 0
⇒ x = 3
Thus, x = 3 is the required solution of the given equation.

(k) \(\frac{k}{8}\) = 8
⇒ k = 8 x 8 = 64
Thus, ft = 64 is the required solution of the given equation.

(l) 13y = 65
y = \(\frac{65}{13}\) = 5
Thus, y = 5 is the required solution of the given equation.

Question 6.
Solve the following riddles, you may yourself construct such riddles. Who am I ?
(i) Go round a square counting every corner thrice and no more. Add the count to me to get exactly thirty four!
(ii) I am a special number. Take away from me a six ! A whole cricket team, you will still be able to fix !
(iii) For each day of the week. Make an up cohnt from me A. If you make no mistake, you will get twenty three !
(iv) Tell “me who I am. I shall give a pretty clue ! You will get me back, if you take me out of twenty two !
Solution:
(i) Let I be V. Since a square has four corners.
Counting every corner thrice, we get 4 x 3 = 12
Now x + 12 = 34
⇒ x = 34 – 12 = 22
Thus, I am 22.

(ii) Let I be ‘x’. By taking away 6 from me, you get x – 6.
∵ There are 11 members in a cricket team.
∴ x – 6 = 11
⇒ x – 11 + 6 = 17.
Thus, I am 17.

(iii) There are 7 days in a week.
∴ A + 7 = 23
⇒ A = 23 – 7 = 16
Thus A = 16.

(iv) Let I be x.
Now, 22 – x = x
⇒ 2x = 22
⇒ x = \(\frac{22}{2}\) = 11
Thus, I am 11.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 Mensuration Intext Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 Mensuration Intext Questions

Question 1.
Measure and write the length of the four sides of the top of your study table. What is the perimeter ?
Solution:

AB = 150 cm
BC = 75 cm
CD = 150 cm
DA = 75 cm
Now, the sum of the L lengths of the four sides
= AB + BC + CD + DA
= 150 cm + 75 cm + 150 cm + 75 cm
= 450 cm
Hence, perimeter = 450 cm.

Question 2.
Measure and write the length of the four sides of a page of your note- book. What is the perimeter of the page?
Solution:
The sum of the lengths of the four sides
= AB + BC + CD + DA
= 20 cm + 15 cm + 20 cm + 15 cm
= 70 cm
Hence, perimeter of the page = 70 cm.

Question 3.
Meera went to a park 150 m long and 80 m wide. She took one complete round of it. What is the distance covered by her ?
Solution:
AB = 150 m,
BC = 80 m
CD = 150 m,
DA = 80 m
∴ Distance covered by Meera
= AB + BC + CD + DA
= 150 m + 80 m + 150 m + 80 m
= 460 m.

Question 4.
Find the perimeter of the following rectangles
Solution:

Question 5.
Biswamitra wants to put coloured tape all around a square picture (Fig. 10.2) of side 1 m as shown. What will be the length of the coloured tape he requires ?
Solution:
Length of one side = 1m
Perimeter of the square = 4 x 1 m = 4 m
Hence, 4 m coloured tape will be required.

Question 6.
Now, look at equilateral triangle (10.3) with each side of 4 cm. Can you find its perimeter ?

Solution:
Length of one side = 4 cm
Perimeter of equilateral triangle = 3 x 4 cm
= 12 cm.

Question 7.
Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.
Solution:
(i) Ignore the portions of the area that are less than half a square.
(ii) If more than half of a square is in a region, just count it as one square.
(iii) If exactly half the square is counted, take it simply as \(\frac{1}{2}\) sq. cm.

Total area = 5 + 1 + 3 = 9sq. cm.

Question 8.
Trace the shape of a leave on the graph paper and estimate its area.
Solution:

Total area = 1 + 1 = 2 sq. cm.

Question 9.
Find the area of the floor of your classroom.
Solution:
Let length of the classroom = 7 m
and breadth of the classroom = 5 m
∴ Area of the classroom
= 7 m x 5 m = 35 sq. m.

Question 10.
Find the area of any one door in your house.
Solution:
Let length of the door = 3 m
and breadth of the door = 1.5 m
∴ Area of the door = 3 m x 1.5 m
= 4.5 sq. m.

Question 11.
Take a piece of 5 cm square paper and find its area.
Solution:
Side of the square = 5 cm
∴ Area of the square = side x side
= 5 cm x 5 cm = 25 cm².

Question 12.
The Jength of one side of a few squares is giyen, find their areas.
Solution:
Length of one side — Area of the square
3 cm = 3 x 3 = 9 sq. cm
7 cm = 7 x 7 = 49 sq. cm
4 cm = 4 x 4 = 16 sq. cm

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 Mensuration Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 Mensuration Exercise 10.2

Question 1.
Find the area of the following figures :

Solution:
(a) This figure is made up of line- segments. Moreover, it is covered by full squares. Here, fully filled squares = 9.
∴ Total area = 9 sq. cm.
(b) This figure is also made up of line- segments. Moreover, it is covered by full squares. Here, fully filled squares 5
∴ Total area = 5 sq. cm.
(c) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.
(i) Fully filled squares = 2.
(ii) Half-filled squares = 4.
∴ Area covered by full squares
= 2 x 1 = 2 sq. cm
and area covered by half squares
= 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 2 + 2 = 4 sq. cm.

(d) This figure is made up of line- segments. Moreover, it is covered by full squares. This makes our job simple.
Here, fully filled squares = 8
∴ Total area = 8 x 1 = 8 sq. cm.

(e) This figure is made up of line-segments. Moreover, it is covered by full squares. Here, fully filled squares = 10
∴ Total area = 10 x 1 = 10 sq. cm.

(f) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.

Here, (i) fully filled squares = 2
(ii) half-filled squares = 4
∴ Area covered by full squares
= 2 x 1 = 2 sq. cm
Area covered by half squares = 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 2 + 2 = 4 sq. cm.

(g) This figure is also made up of line- segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 4
(ii) half-filled squares = 4

∴ Area covered by full squares
= 4 x 1 = 4 sq. cm
Area covered by half squares
= 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 4 + 2 = 6 sq. cm.

(h) This figure is made up of line- segments. Moreover, it is covered by full squares only. This makes our job simple.
Here, fully filled squares = 5
∴ Total area = 5 x 1 sq. cm = 5 sq cm.

(i) This figure is made up of line-segments. Moreover, it is covered by full squares only. This makes our job simple.
Here, fully filled squares = 9
∴ Total area = 9 x 1 sq. cm = 9 sq. cm.

(j) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 2

(ii) half-filled squares = 4
∴ Area covered by full squares = 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence,
total area = (2 + 2) sq. cm :
= 4 sq. cm.

(k) This figure is made up of line segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 4
(ii) half filled squares = 2
∴ Area covered by full squares
= 4 x 1 = 4 sq. cm
Area covered by half squares
= 2 x \(\frac{1}{2}\) = 1 sq. cm ,
Hence,
total area = (4+1) sq. cm
= 5 sq. cm.

(l)

Total area = 4 + 1 + 3 + 0 = 8sq. cm.

(m)

Total area = 8 + 1 + 4 + 0 = 13 sq. cm.

(n)

∴ Total area = 13 + 1 + 3 + 0 = 17 sq. cm.

Question 2.
Use tracing paper and centimeter graph paper to compare the areas of the following pair of figures :

Solution:
(a)

∴ Total area = 3 + 1 + 8 + 0 = 12 sq. cm.

(b)

Total area = 6 + 1\(\frac{1}{2}\) + 7 + 0 = 14\(\frac{1}{2}\) sq. cm.
Thus, area in Fig.(b) is greater than the area in Fig.(a).

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 Mensuration Ex 10.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 Mensuration Exercise 10.3

Question 1.
Find the area of the rectangles whose sides are :
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm.
Solution:
(a) Length of the rectangle (l) = 4 cm
Breadth of the rectangle (b) = 3 cm
.’. Area of the rectangle = l x b
= 4 cm x 3 cm
= 12 sq. cm.

(b) Length of the rectangle (l) = 21 m
Breadth of the rectangle (b) = 12 m
Area of the rectangle = l x b
= 21 m x 12 m
= 252 sq. m.

(c) Length of the rectangle (l) = 3 km
Breadth of the rectangle (b) = 2 km
∴ Area of the rectangle = l x b = 3km x 2km = 6 sq. km.

(d) Length of the rectangle (l)
= 2 m = 200 cm
Breadth of the rectangle (b) = 70 cm
∴ Area of the rectangle = l x b
= 200 x 70 sq. cm
= 14,000 sq. cm.

Question 2.
Find the areas of the squares whose sides are :
(a) 10 cm
(b) 14 cm
(c) 5 m.
Solution:
(a) Side of the square = 10 cm
∴ Area of the square = side x side
= 10 cm x 10 cm
= 100 sq. cm.

(b) Side of the square = 14 cm
∴ Area of the square = side x side
= 14 cm x 14 cm – 196 sq. cm.

(c) Side of the square = 5 m
.’. Area of the square = side x side
= 5 m x 5 m
= 25 sq. m.

Question 3.
Three rectangles have the following dimensions :
(a) 9 m and 6 m
(b) 3 m and 17 m
(c) 4 m and 14 m.
Which one has the largest area and which one has the smallest ?
Solution:
(a) Length of the rectangle = 9 m
Breadth of the rectangle = 6 m
.’. Area of the rectangle = length x breadth
= 9 m x 6 m = 54 sq. m.

(b) Length of the rectangle (l) = 17 m
Breadth of the rectangle (b) = 3 m
∴ Area of the rectangle = l x b
= 17 m x 3 m = 51 sq. m.

(c) Length of the rectangle (l) = 14 m
Breadth of the rectangle (b) = 4 m
∴ Area of the rectangle = l x b
= 14 m x 4 m = 56 sq. m.
Rectangle (c) has the largest area and rectangle (b) has the smallest area.

Question 4.
The area of a rectangular garden 50 m long is 300 sq. m. Find the width of the garden.
Solution:
Area of the rectangle = 300 sq. m
Length of the rectangle = 50 m
Width of the rectangle = ?

∴ Area of the rectangle = length x width
∴ Width = \(\frac{\text { Area }}{\text { length }}=\frac{300}{50}\) = 6 cm
Hence, width of the rectangle = 6 m.

Question 5.
What is the cost of tiling a rect¬angular piece of land 500 m long and 200 m wide at the rate of Rs. 8 per hundred sq. m.
Solution:
Total area of the tiles must be equal to the area of the land.
Length of the land (l) = 500 m
Breadth of the land (b) = 200 m

∴ Area of the land = l x b
= 500 m x 200 m
Area of the tiles = 1,00,000 sq.m
Cost of 100 sq. m tiles = Rs. 8
Cost of 1 sq. m tiles = Rs. \(\frac{8}{100}\)
Cost of 1,00,000 sq. m tiles 8
= Rs. \(\frac{8}{100}\) x 1,00,000 = Rs. 8,000.

Question 6.
A table measures 2 m 25 cm by 1 m 50 cm. What is its area in square metres ?
Solution:
Length of the table (l) = 2.25 m
Breadth of the table (b) = 1.50 m

∴ Area of the table = lx b
= 2.25 x 1.50 sq. m
= 3.375 sq. m.

Question 7.
A room is 4 m 20 cm long and 3 m 65 cm wide. How many square metres of carpet is needed to cover the floor of the room ?
Solution:
Length of the room (l) = 4.20 m
Breadth of the room (b) = 3.65 m

∴ Area of the room = l x b
= 4.20 x 3.65 sq. m
= 15.33 sq. m
Hence, area of the carpet needed to cover the floor of the room = 15.33 sq. m.

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
Length of the floor (l) = 5 m
Breadth of the floor (b) = 4 m

∴ Area of the floor = l x b
= 5 x 4 sq. m
= 20 sq. m
Side of the square carpet = 3 m
∴ Area of the square carpet = 3 m x 3 m
= 9 sq. m
Hence, area of the floor that is not carpeted = 20 – 9 = 11 sq. m.

Question 9.
Five square flower beds each of sides 1.2 m are dug on a piece of land 4.8 m long and 4.2 m wide. What is the area of the remaining part of land ?
Solution:
Length of the land (l) = 4.8 m
Bread of the land (b) = 4.2 m

∴ Area of the land = l x b
= 4.8 m x 4.2 m
= 20.16 sq. m.
Side of one square flower bed = 1.2 m
∴ Area of one square flower bed
= 1.2 m x 1.2 m
= 1.44 sq. m
∴  Area of the square flower beds
= 5 x 1.44 sq. m
= 7.20 sq. m
Hence, area of the remaining part of the land
= 20.16 sq. m – 7.20 sq. m = 12.96 sq. m.

Question 10.
The following figures have been split into rectangles. Find their areas (The measures are given in centimetres).

Solution:
(a) Total area of the given figure
= (3×3 + lx2 + 3×3 + 4×2)sq. m = (9 + 2 + 9 + 8) sq. cm
= 28 sq. cm

(b) Total area of the given figure
= (2 x 1 + 5 x 1 + 2 x 1) sq. cm
= (2 + 5 + 2) sq. cm = 9 sq. cm.

Question 11.
Split the following shapes into rectangles and find the area of each. (The measures are given in centimetres).

Solution:
(a) Total area of the given figure
= (10 x 2 + 10 x 2) sq. cm = (20 + 20) sq. cm = 40 sq. cm
(b) Total area of the given figure
= (7 x 7 + 21 x 7 + 7 x 7) Sq. cm = (49 + 147 + 49) sq. cm = 245 sq. cm.
(c) Total area of the given figure
= (4 x 1 + 5 x 1) sq. cm = (4 + 5) sq. cm = 9 sq. cm.

Question 12.
How many tiles with dimensions 5 cm and 12 cm will be needed to fit a region whose length and breadth are respectively :
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm.
Solution:
(a) Length of the region (l) = 144 cm
Breadth of the region (b) = 100 cm

∴ Area of the region = 144 x 100
= 14400 sq. cm
Length of one tile = 12 cm
Breadth of one tile = 5 cm
∴ Area of one tile = 12 x 5
= 60 sq. cm
Number of tiles required = \(\frac{\text { Area of the region }}{\text { Area of one tile }}=\frac{14400}{60}\) = 240 tiles.

(b) Length of the region (l) = 70 cm
Breadth of the region (b) = 36 cm

∴ Area of the region = 70 x 36 sq.cm
= 2520 sq.cm
Length of one tile = 12 cm
Breadth of one tile = 5 cm
∴ Area of one tile = 12 x 5 = 60 sq. cm
Number of tiles required = \(\) = 42 tiles

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 Mensuration Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 Mensuration Exercise 10.1

Question 1.
Find the perimeter of each of the following figures :

Solution:
(a) Perimeter = 5 cm + 1 cm + 2 cm + 4 cm = 12 cm.
(b) Perimeter = 40 cm + 35 cm + 23 cm + 35 cm = 133 cm.
(c) Perimeter = 15 cm +15 cm + 15 cm + 15 cm = 60 cm.
(d) Perimeter = 3 cm + 3 cm + 3 cm + 3 cm + 3 cm = 15 cm.
(e) Perimeter = 1 cm + 4 cm + 0.5 cm + 2.5 cm + 2.5 cm + 0.5 cm + 4 cm = 15 cm.
(f) Perimeter = 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm
= 52 cm.

Question 2.
The lid of a rectangular box of sides 40 cm by 10 cm is sealed all around with tape. What is the length of the tape required ?

Solution:
Length of the rectangular box (l) = 40 cm
Breadth of the rectangular box (b) = 10 cm
Perimeter of the rectangular box
= 2 x (l + b)
= 2 x (40 + 10) cm
= 2 x 50 = 100 cm
Hence, length of the tape required = 100 cm or 1m.

Question 3.
A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the top of the table ?

Solution:
Length of the table-top (l)
= 2 m 25 cm
= 2.25 m
Breadth of the table-top (b)
= 1 m 50 cm
= 1.50 m
Perimeter of the table-top
= 2 x (l + b)
= 2 x (2.25 + 1.50) m
= 2 x 3.75
= 7.50 m.

Question 4.
What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively ?

Solution:
Length of the frame (l)
= 32 cm
Breadth of the frame (b)
= 21 cm
Perimeter of the frame
= 2 x (l + b)
= 2 x (32 cm + 21 cm)
= 2 x 53 cm
= 106 cm.
Hence, length of the wooden strip required to frame a photograph = 106 cm.

Question 5.
A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of wire needed ?
Solution:
Length (l) = 0.7 km
Breadth (b) = 0.5 km
Perimeter – 2 x (l + b)
= 2 x (0.7 + 0.5) km
= 2 x 1.2 = 2.4 km

Length of wire needed to fence with 4 rows = 4 x 2.4 = 9.6 km.

Question 6.
Find the perimeter of each of the following shapes :
(a) A triangle of sides 3 cm, 4 cm and 5 cm.
(b) An equilateral triangle of side 9 cm.
(c) An isosceles triangle with equal sides 8 cm each and third side 6 cm.
Solution:
(a) Perimeter of the triangle
= 3 cm + 4 cm + 5 cm = 12 cm.

(b) One side of an equilateral
Δ = 9 cm

.’. Perimeter of the triangle
= 3 x length of one side
= 3 x 9 cm = 27 cm.

(c) Perimeter of isosceles triangle
= 8 cm + 8 cm + 6 cm
= 22 cm.

Question 7.
Find the peri-meter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Solution:
Perimeter of the triangle
= 10 cm + 14 cm + 15 cm
= 39 cm.

Question 8.
Find the perimeter of a regular hexagon with each side measuring 8 m.
Solution:
One side of a regular hexagon = 8 m

Perimeter of regular hexagon = 6 x one side
= 6 x 8 m
= 48 m.

Question 9.
Find the side of a square whose perimeter is 20 m.

Solution:
Let, one side of a square = am
Perimeter of the square = 20 m
4 x a = 20
a = \(\frac{20}{4}\) = 5 cm
Hence, one side of the square = 5 m.

Question 10.
The perimeter of a regular pentagon is 100 cm. How long is each side?
Solution:
Let one side of the regular pentagon = a cm
Perimeter of the regular pentagon = 100 cm
5 x a = 100
=> a = \(\frac{100}{5}\) = 20 cm.
Hence, each side of a regular pentagon = 20 cm.

Question 11.
A piece of string is 30 cm long. What will be the length of each side if the string is used to form :
(a) a square ?
(b) an equilateral triangle ?
(c) a regular hexagon ?

Solution:
(a) Let one side of a square = a cm
Perimeter of the square = 30 cm
4 x a = 30 cm
=> a = \(\frac{30}{4}\) cm = 7.5 cm
Hence, length of each side of the square = 7.5 cm.

(b) Let each side of the equilateral Δ = a cm
Perimeter of the equilateral Δ = 30 cm
3 x a = 30 cm
a = \(\frac{30}{3}\)
= 10 cm

Hence, each side of the equilateral Δ = 10 cm.

(c) Let each side of the regular hexagon
= a cm

Perimeter of the regular hexagon = 30 cm
6 x a = 30 cm
=> a = \(\frac{30}{6}\) = 5 cm

Question 12.
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is the third side ?
Solution:
Let the third side of a triangle = x cm

Perimeter of the triangle = 36 cm
.-. 14 cm + 12 cm + x cm = 36 cm
=> 26 cm + x cm = 36 cm
x = 36 – 26 = 10 cm
Hence, the third side of the triangle = 10 cm.

Question 13.
Find the cost of fencing a square park of side 250 m at the rate of Rs. 20 per metre.

Solution:
Each side of the square park = 250 m
Perimeter of the square park
= 4 x 250 m
= 1000 m
Cost of one metre of wire = Rs. 20
Cost of fencing the square park = Rs. 20 x 1000
= Rs. 20,000.

Question 14.
Find the cost of fencing a rectangular park of length 175 m and breadth 125 m at the rate of Rs. 12 per metre.
Solution:
Length of the rectangular park (l) = 175 m
Breadth of the rectangular park (b) = 125 m
Perimeter of the rectangular park . = 2 x (l + b)
= 2 x (175 + 125) m
= 2 x 300
= 600 m
Cost of one metre of wire = Rs. 12
.•. Cost of fencing the rectangular park
= Rs. 12 x 600
= Rs. 7200.

Question 15.
Sweety runs around a square park of side 75 m. Bulbul runs around a rectangle with length 60 metre and breadth 45 metre. Who covers less distance ?
Solution:

Each side of the square park = 75 m
Perimeter of the square park = 4 x 75 = 300 m
.’. Distance covered by Sweety = 300 m
Now, length of the rectangular park (l)
= 60 m
breadth of the rectangular park (b) = 45 m
Perimeter of the rectangular park = 2 x (l+ b)
= 2 x (60 + 45)
= 2 x 105 = 210 m
Distance covered by Bulbul = 210 m
Hence, Bulbul covers less distance.

Question 16.
What is the perimeter of each of the following figures ? What do you infer from the answers ?

Solution:
(a) One side of the square = 25 cm
Perimeter of the square
=4 x 25 = 100 cm.

(b) Length of the rectangle (l) = 40 cm
Breadth of the rectangle (b) = 10 cm
Perimeter of the rectangle = 2 x (l + b)
= 2 x (40 + 10) cm
= 2 x 50 = 100 cm.

(c) Length of the rectangle (l) = 30 cm
Breadth of the rectangle (b) = 20 cm
.’. Perimeter of the rectangle
= 2 x (l + b)
= 2 x (30 + 20) cm
= 2 x 50 = 100 cm.

(d) Sides of the triangle are 40 cm, 30 cm and 30 cm.
Perimeter of the triangle
= 40 cm + 30 cm + 30 cm
= 100 cm.
We infer from the answers that all the figures have the same perimeter.

Question 17.
Avneet buys 9 square paving slabs, each of a side of 1/2 m. He lays them in the form of a square.


(a) What is the perameter of his arrangement [Fig. 10.24(a)]?
(b) Shari does not like his arrangement.
She gets him to lay them out like a cross [Fig. 10.24(b)]. What is the perimeter of her arrangement ?
(c) Which has a greater perimeter ?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this ? (The paving slabs must meet along complete edges, they cannot be broken).
Solution:

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 Data Handling Ex 9.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 Data Handling Exercise 9.4

Question 1.
A survey of 120 school students was done to find which activity they prefer to do in their free time. Draw a bar graph to illustrate the given data taking scale of 1 unit length = 5 students.

Which activity is preferred by most of the students other than playing ?

Solution:
Reading books is preferred by most of the students other than playing.

Question 2.
Following table shows the number of bicycles manufactured in a factory during the years 1998 to 2002. Illustrate this data using a bar graph. Choose a scale of your choice.
Years — No. Manufactured of Bicycles
1998 — 800
1999 — 600
2000 — 900
2001 — 1100
2002 — 1200
(a) In which year were the maximum number of bicycles manufactured ?
(b) By looking at the bar graph, write which two years show the maximum rise in the manufacture of bicycles ?
Solution:
(a) In 2002, maximum number of bicycles were manufactured.

(b) 2000 and 2001 show the maximum rise in the manufacture of bicycles.

Question 3.
Number of persons in various age groups in a town is given in the following table :
Age group — No. of persons
1-14 — 2 lakh
15-29 — 1 lakh 60 thousand
30-44 — 1 lakh 20 thousand
45-59 — 1 lakh 20 thousand
60-74 — 80 thousand
75 and above — 40 thousand
Draw the bar graph to represent the above information and answer the following questions (take 1 unit length = 20 thousand)
(a) Which two age groups have the same population ?
(b) All persons in the age group of 60 and above are called senior citizens. How many senior citizens are there in the town ?
Solution:

(а) 30-44 and 45-59 have the same population.
(b) .80,000 + 40,000 = 1,20,000 are senior citizens.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 Data Handling Ex 9.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 Data Handling Exercise 9.3

Question 1.
Bar graph given below shows the amount of wheat purchased by government during the year 1998-2002.

Read the bar graph andi write down your observations.
Solution:
Year — Amount of wheat purchased
1998 — 15 thousand tons
1999 — 25 thousand tons
2000 — 20 thousand tons
2001 — 20 thousand tons
2002 — 30 thousand tons

Question 2.
Observe this bar graph which is showing the sale of shirts in a ready¬made shop from Monday to Saturday. Now answer the following questions :

(a) What information is given by the above bar graph ?
(b) Mention the scale chosen on the vertical line representing the no. of shirts.
(c) Mention the day on which the maximum number of shirts were sold and also mention the number of shirts sold.
(d) Mention the day on which the minimum number of shirts were sold.
(e) How many shirts were sold on Thursday ?
Solution:
(a) This bar graph shows the number of shirts sold from Monday to Saturday.
(b) 1 unit = 5 shirts.
(c) The maximum no. of shirts 60 were sold on Saturday.
(d) The minimum no. of shirts were sold on Tuesday.
(e) On Thursday, 35 shirts were sold.

Question 3.
Observe this bar graph which is showing the marks obtained by Aziz in half-yearly examination in different subjects. Answer the questions given below :

(a) What information is given by the bar graph ?
(b) Name the subject in which Aziz has scored maximum marks ?
(c) Name the subject in which he has scored minimum marks ?
(d) State the names of the subjects and marks obtained in each of them ?
Solution:
(a) This bar graph shows the marks obtained by Aziz in different subjects.
(b) Hindi (c) Social Studies
(d) Subjects — Marks obtained
(i) Hindi — 80
(ii) English — 60
(iii) Mathematics — 70
(iv) Science — 65
(v) Social Studies — 55

Question 4.
Following is a bar graph of circu¬lation of newspapers (dailies) in a town in six languages. Study the bar graph and answer the following questions :

(a) Find the number of newspapers circulated in Hindi, Punjabi, Urdu, Marathi and Tamil.
(b) Name the language in which the least no. of newspapers are circulated.
(c) What is the difference between the no. of Hindi and English papers being read ?
(d) Write the no. of newspapers circulated in different languages in ascending order.
Solution:
(a) Hindi—800, Punjabi—400, Urdu—200, Marathi—300, Tamil—100.
(b) Least no. of newspapers are circulated in Tamil.
(c) Difference between Hindi and English papers = 800 -500 = 300.
(d) 100, 200, 300, 400, 500, 800.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 Data Handling Ex 9.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 Data Handling Exercise 9.2

Question 1.
Total number of animals in five villages are as follows :
Village A : 80
Village B : 120
Village C : 90
Village D : 40
Village E : 60
Prepare a pictograph of these animals using one symbol 0 to represent 10 animals and answer the following questions :
(a) How many symbols represent animals of village E ?
(b) Which village has the maximum number of animals ?
(c) Which village has more animals : village A or village C ?
Solution:

(a) 6, (6) B, (c) C.

Question 2.
Total number of students of a school in different years is shown in the following table :
Year — Number of students
1996 — 400
1998 — 535
2000 — 472
2002 — 600
2004 — 623
A. Prepare a pictograph of students using one symbol represent 100 students and answer the following questions :
(a) How many symbols represent total number of students in the year 2002 ?
(b) How many symbols represent total number of students for the year 1998 ?
Solution:

(a) 6, (b) 5 complete and 1 incomplete.

B. Prepare another pictograph of students using any other symbol each representing 50 students. Which pictograph do you find more informative ?
Solution:

Second pictograph is more informative.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 Data Handling Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 Data Handling Exercise 9.1

Question 1.
In a mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.
(a) Find how many students obtained marks equal to or more than 7 ?
(b) How many students obtained marks below 4 ?

Solution:

(a) 12 students obtained marks equal to or more than 7.
(b) 8 students obtained marks below 4.

Question 2.
Following is the choice of sweets of 30 students of class VI.
Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla,
Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi,
Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo,
Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla,
Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo
(a) Arrange the names of sweets in a table using tally marks.
(b) Which sweet is preferred by most of the students ?
(c) Choose any symbol representing one student and make apictograph showing the choices.
Solution:

(b) Ladoo is preferred by most of the students.
(c) Pictograph.

Question 3.
Following pictograph shows the number of tractors in 5 villages :

Observe the pictograph and answer the following questions :
(i) Which village has the minimum number of tractors ?
(ii) Which village has the maximum number of tractors ?
(iii) How many more tractors village C has as compared to village B ?
(iv) What is the total number of tractors in all the five villages ?
Solution:
(i) Village D has minimum number of tractors.
(ii) Village C has maximum number of tractors.
(iii) Village C has 3 more tractors as compared to village B.
(iv) 6 + 5 + 8 + 3 + 6 = 28. The total number of tractors in all the five villages = 28.

Question 4.
The sale of electric bulbs on different days of a week is shown below :

Observe the pictograph and answer the following questions :
(a) How many bulbs were sold on Friday ?
(b) On which day were the maximum num ber of bulbs sold ?
(c) If one bulb were sold at the rate ofRs. 10, what was the total sale on Sunday ?
(d) Can you find out the total sale of the week ?
(e) If one big carton can hold 9 bulbs, how many cartons were needed in the given week, more than 4, more than 5 or more than 6 ?
Solution:
(a) 7 x 2 = 14 bulbs were sold on Friday.
(b) The maximum number of bulbs (18) were sold on Sunday.
(c) Total sale on Sunday = Rs. 10 x 18 = Rs. 180.
(d) Total sale of the week = Rs. 10 x 86 = Rs. 860.
(e) No. of cartons needed = 86 ÷ 9 = 9\(\frac{5}{9}\), i.e. more than 6.

Question 5.
The number of girl students in each class of a co-ed middle school is depicted by the following pictograph :

Observe this pictograph and answer the following questions :
(a) Which class has the minimum number of girl students ?
(b) Is the number of girls in class VI less than the number of girls in class V ?
(c) How many girls are there in class VII ?
(d) What other inferences can you draw from this pictograph ?
Solution:
(a) Class VIII has the minimum number of girl students (6).
(b) No, the number of girl students in class VI are not less than the number of girls in class V.
(c) In class VII, there are 12 girl students.
(d) This pictograph shows that the maximum number of girl students (24) are in class I and the total number of girls in the school are 120.

Question 6.
In a village, six fruit merchants sold the following number of fruit baskets in a particular season :

Observe this pictograph and answer the following questions :
(a) Which merchant sold the maximum number of baskets ?
(b) How many fruit baskets were sold by Anwar ?
(c) The merchants who have sold 600 or more number of baskets are planning to buy a godown for the next season. Can you name them ?
Solution:
(a) Martin sold the maximum number of baskets.
(b) 700 fruit baskets were sold by Anwar.
(c) Anwar, Martin and Ranjit Singh.