Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 Mensuration Ex 10.2 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 10 Mensuration Exercise 10.2
Question 1.
Find the area of the following figures :
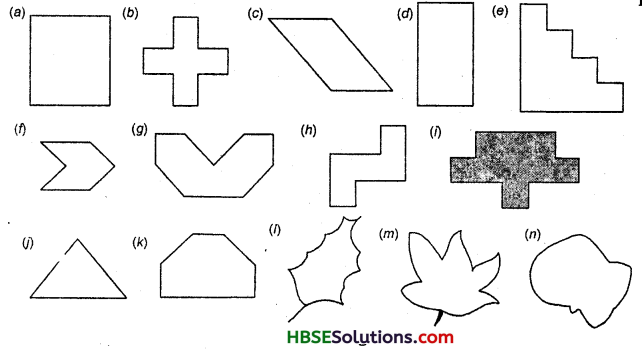
Solution:
(a) This figure is made up of line- segments. Moreover, it is covered by full squares. Here, fully filled squares = 9.
∴ Total area = 9 sq. cm.
(b) This figure is also made up of line- segments. Moreover, it is covered by full squares. Here, fully filled squares 5
∴ Total area = 5 sq. cm.
(c) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.
(i) Fully filled squares = 2.
(ii) Half-filled squares = 4.
∴ Area covered by full squares
= 2 x 1 = 2 sq. cm
and area covered by half squares
= 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 2 + 2 = 4 sq. cm.
(d) This figure is made up of line- segments. Moreover, it is covered by full squares. This makes our job simple.
Here, fully filled squares = 8
∴ Total area = 8 x 1 = 8 sq. cm.
![]()
(e) This figure is made up of line-segments. Moreover, it is covered by full squares. Here, fully filled squares = 10
∴ Total area = 10 x 1 = 10 sq. cm.
(f) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 2
(ii) half-filled squares = 4
∴ Area covered by full squares
= 2 x 1 = 2 sq. cm
Area covered by half squares = 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 2 + 2 = 4 sq. cm.
(g) This figure is also made up of line- segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 4
(ii) half-filled squares = 4
∴ Area covered by full squares
= 4 x 1 = 4 sq. cm
Area covered by half squares
= 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence, total area = 4 + 2 = 6 sq. cm.
(h) This figure is made up of line- segments. Moreover, it is covered by full squares only. This makes our job simple.
Here, fully filled squares = 5
∴ Total area = 5 x 1 sq. cm = 5 sq cm.
(i) This figure is made up of line-segments. Moreover, it is covered by full squares only. This makes our job simple.
Here, fully filled squares = 9
∴ Total area = 9 x 1 sq. cm = 9 sq. cm.
(j) This figure is made up of line-segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 2
(ii) half-filled squares = 4
∴ Area covered by full squares = 4 x \(\frac{1}{2}\) = 2 sq. cm
Hence,
total area = (2 + 2) sq. cm :
= 4 sq. cm.
![]()
(k) This figure is made up of line segments. Moreover, it is covered by full squares and half squares only.
Here, (i) fully filled squares = 4
(ii) half filled squares = 2
∴ Area covered by full squares
= 4 x 1 = 4 sq. cm
Area covered by half squares
= 2 x \(\frac{1}{2}\) = 1 sq. cm ,
Hence,
total area = (4+1) sq. cm
= 5 sq. cm.
(l)
| Cover | Number | Area estimated (sq. cm) |
| (i) Fully-filled squares | 4 | 4 |
| (ii) Half-filled squares | 2 | 2 x \(\frac{1}{2}\) = 1 |
| (Hi) More than half-filled squares | 3 | 3 |
| (iv) Less than half-filled squares | 3 | 0 |
Total area = 4 + 1 + 3 + 0 = 8sq. cm.
(m)
| Cover | Number | Area estimated (sq. cm) |
| (i) Fully filled squares | 8 | 8 |
| (ii) Half-filled squares | 2 | 2 x \(\frac{1}{2}\) = 1 |
| (Hi) More than half-filled squares | 4 | 4 |
| (iv) Less than half-filled squares | 6 | 0 |
Total area = 8 + 1 + 4 + 0 = 13 sq. cm.
(n)
| Cover | Number | Area estimated (sq. cm) |
| (i) Fully filled squares | 13 | 13 |
| (ii) Half-filled squares | 2 | 2 x \(\frac{1}{2}\) = 1 |
| (Hi) More than half-filled squares | 3 | 3 |
| (iv) Less than half-filled squares | 5 | • 0 |
∴ Total area = 13 + 1 + 3 + 0 = 17 sq. cm.
![]()
Question 2.
Use tracing paper and centimeter graph paper to compare the areas of the following pair of figures :
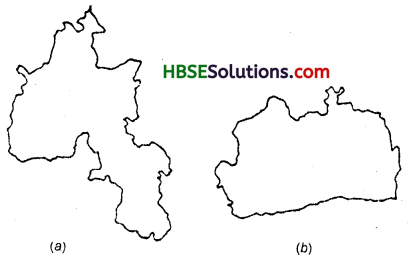
Solution:
(a)
| Cover | Number | Area estimated (sq. cm) |
| (i) Fully filled squares (√) | 3 | 3 |
| (ii) Half-filled squares (.) | 2 | 2 x \(\frac{1}{2}\) = 1 |
| (iii) More than half-filled squares (Δ) | 8 | 8 |
| (iv) Less than half-filled squares (x) | 7 | 0 |
∴ Total area = 3 + 1 + 8 + 0 = 12 sq. cm.
(b)
| Cover | Number | Area estimated (sq. cm) |
| (i) Fully filled squares (√) | 6 | 6 |
| (ii) Half-filled squares (.) | 3 | 3 x \(\frac{1}{2}\) = 1\(\frac{1}{2}\) |
| (iii) More than half-filled squares (Δ) | 7 | 7 |
| (iv) Less than half-filled squares (x) | 6 | 0 |
Total area = 6 + 1\(\frac{1}{2}\) + 7 + 0 = 14\(\frac{1}{2}\) sq. cm.
Thus, area in Fig.(b) is greater than the area in Fig.(a).