Class 8

Haryana Board HBSE Class 8 Solutions in Hindi Medium & English Medium

• HBSE 8th Class Maths Solutions
• HBSE 8th Class Science Solutions
• HBSE 8th Class Social Science Solutions
• HBSE 8th Class English Solutions
• HBSE 8th Class Hindi Solutions
• HBSE 8th Class Sanskrit Solutions

Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 16 Playing with Numbers InText Questions

Try These (Page 250)

Question 1.
Write the following numbers in generalised form :
(i) 25
(ii) 73
(iii) 129
(iv) 302.
Solution:
(i) 25 = 2 × 10 + 5
[∵ ab = 10 × a + b where a and b are tens and ones place digits]
(ii) 73 = 7 × 10 + 3 ∵ ab = 10 × a + b]
(iii) 129 = 1 × 100 + 2 × 10 + 1 × 9
[∵ abc = 100 × a + 10 × b + 1 × c where a, b, c are hundreds, tens and ones place digits]
(iv) 302 = 100 × 3 + 0 × 10 + 1 × 2.

Question 2.
Write the following in the usual form :
(i) 10 × 5 + 6
(ii) 100 × 7 + 10 × 1 + 8
(iii) 100 × a + 10 × c + b.
Solution:
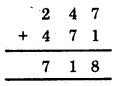
(i) 10 × 5 + 6 = 50 + 6 = 56
(ii) 100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718
(iii) 100 × a + 10 × c + b = 100a + 10c + b.

Try These (Page 251)

Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below :
1. 27
2. 39
3. 64
4. 17
Solution:

Conclusion : It is obvious from the above games with numbers that remainder is zero in each cases if we follow the procedure explained above. Quotient is always (a + b) i.e. 2 + 7 = 9 and so on.

Question 2.
Check what the result would have been if Sundaram had chosen the numbers shown below :
1. 17
2. 21
3. 96
4. 37.
Solution:

Hence, we observe that the quotient in each cases is either (a – b) or (b – a) according as a > b or a

Try These (Page 252)

Question 1.
Check what the result would have been if Minakshi had chosen the numbers shown below. In each case keep a record of the quotient obtained at the end.
1. 132
2. 469
3. 737
4. 901.
Solution:
1. Let the Minakshi had chosen the 3-digit number 132. So she got:
Reversed number : 231
Difference : 231 – 132 = 99
Division by 99 : 99 ÷ 99 = 1, with no remainder
Hence, Quotient = 1, Remainder = 0

2. Here,
Original number : 469
Difference : 964 – 469 = 495
Reversed number : 964
Division (by 99) : 495 ÷ 99 = 5
∴ Quotient = 5, Remainder = 0 (i.e. No remainder).

3. Here
Original number : 737
Reversed number : 737
Difference : 737 – 737 = 0
Division (by 99) : 0 ÷ 99 = 0 with no remainder
Hence, Quotient = 0, Remainder = 0

4. Here
Original number : 901
Reversed number : 109
Difference : 901 – 109 = 792
Division (by 99) : 792 ÷ 109 = 0 with no remainder
Hence, Quotient = 8, Remainder = 0
Conclusion : Hence, the resulting number is divisible by 99 in each cases and the quotient obtained is [(c – a) or (a – c)]. So, the remainder is zero.

Try These (Page 253)

Question 1.
Check what the result, would have been if Sundaram had chosen the numbers shown below :
1. 417
2. 632
3. 117
4. 937
Solution:
1. Original dumber
= 417 [It is in the form abc]
The number obtained by changing the digits like (cab)
= 741
and the other number in the form (bca) = 174
[Here, a = 4, b = 1 and c = 7]
Now add them up :

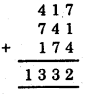
Then, we divide the resulting number 1332 by 37
∴ 1332 ÷ 37 = 36, with no remainder.
Hence, the number is divisible by 37 and remainder is 0.

2. Here, abc = 632
[∵ a = 6, b = 3 and c = 2]
cab = 263
and bca = 326
Add them up :

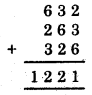
Divide the number by 37.
1221 ÷ 37 = 33, with no remainder.
∴ The number so obtained is divisible by 37.
Thus, Quotient = 33, Remainder = 0.

3. Here, abc =117
[Here a = 1, b = 1 and c = 7] c
ab = 711
and bca = 171
Add them up :

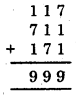
Divide the number by 37.
999 ÷ 37 = 27, with no remainder.
∴ The resulting number is divisible by 37.
Thus, Quotient = 27, Remainder = 0.

4. We have abc = 937
[Here a = 9, b = 3 and c = 7]
cab = 793
and bca = 379
Add them up:

Divide the number so obtained by 37.
2109 + 37 = 57, with no remainder.
∴ The resulting number is divisible by 37. Thus, Quotient = 57, Remainder = 0.

Try These (Page 255)

Question 1.
Write a 2-digit number ab and the number obtained by reversing its digits i.e., ba. Find their sum. Let the sum be a 3¬digit number dad
i.e. ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
(i) The sum a + b can not exceed 18 (why) ?
(ii) Is dad a multiple of 11 ?
(iii) Is dad less than 198 ?
(iv) Write all the 3-digit num bers which are multiples of 11 upto 198.
Find the values of a and d.
Solution:
Let a 2-diglt number be 87.
Then, the number obtained by reversing it will be 78.
Sum of these two numbers i.e. ab + ba = 87 + 78 = 165
165 is a 3-digit number.
Sum of digits = a + 6 = 8 + 7 = 15 which is less than 18.

(i) Take the maximum value of 2-digit number which is 99.
Even then, ab + ba = 99 + 99 = 198
So, a + b = \(\frac{198}{11}\) = 18
[∵ 11(a + b) = dad]
Thus, a + b can not exceed 18.
(ii) Yes, it is a multiple of 11.
(iii) Yes, it is less than 198.
(iv) 3-digits numbers which are multiples of 11 are :
11 × 10 = 110 Here, dad = 110, ∴ d = 1 or 0, a = 1
11 × 11 = 121; dad = 121 a = 2, d = 1
11 × 12 = 132; a = 3, d = 1 or 2
11 × 13 = 143; a = 4, d = 1 or 3
11 × 14 = 154; a = 4, d = 1 or 4
11 × 15 = 165; a = 6, d = 1 or 5
11 × 16 = 176; a = 7, d = 1 or 6

Try These (Page 257)

Question 1.
If the division N + 5 leaves a remainder of 3, what might be the ones digit of N ?
Answer:
The one’s digit, when divided by 5, must leave a remainder of 3. So the one’s digit must be either 3 or 8.

Question 2.
If the division N + 5 leaves a remainder of 1, what might be the one’s digit of N ?
Answer:
The one’s digit when divided by 5, must leave a remainder 1.
∴ The one’s digit must be either 1 or 6.

Question 3.
If the division N + 5 leaves a remainder of 4, what might be the one’s digit of N ?
Answer:
The one’s digit must be either 4 or 9.
For example,

Try These (Page 257-258)

Question 1.
If the division N + 2 leaves a remainder of 1, what might be the one’s digit of N ?
Answer:
N is odd; so ;its one’s digit is odd. Therefore, the one’s digit must be 1, 3, 5, 7 or 9.

Question 2.
If the division N + 2 leaves a remainder (t.e., zero remainder), what might be the one’s digit of N ?
Answer:
The one’s digit of N must be 0, 2, 4, 6 or 8 i.e. an even number.

Question 3.
Supose that the division N + 5 leaves a remainder of 4, and the division N + 2 leaves a remainder of 1. What must be the one’s digit of N ?
Answer:
∵ N ÷ 5 leaves a remainder 4.
∴ One’s digit of N should be 4 or 9.
Now, N ÷ 2 leaves a remainder of 1
∴ One’s digit of N are 1, 3, 5, 7, 9.
9 is a common digit in both the cases.
∴ One’s, digit of N must be 9.

Try These (Page 259)

Question 1.
Check the divisibility of the following numbers by 9 :
1. 108
2. 616
3. 294
4. 432
5. 927.
Solution:
(1) The sum of the digits of 108 is 1 + 0 + 8 = 9
So, this number is divisible by 9 because the sum of its digits is divisible by 9.

(2) The sum of the digits of 616 is 6 + 1 + 6 = 13
∵ 13 is not divisible by 9,
∴ Thus no. is also not divisible by 9.

(3) The sum of the digits of 294 is 2 + 9 + 4 = 15
∵ 15 is not divisible by 9.
∴ 294 is not divisible by 9.

(4) The sum of the digits 432 is 4 + 3 + 2 = 9.
∵ Sum of the digits i.e. 9 is divisible by 9.
∴ 432 is divisible by 9.

(5) The sum of the digits of 927 is 9 + 2 + 7 = 18
So, this number is divisible by 9 because sum of the digits i.e. 18 is divisible by 9.

Think, Discuss and Write (Page 259)

Question 1.
You have seen that a number 450 is divisible by 10. It is also divisible by 2 and 5 which are factors of 10. Similarly, a number 135 is divisible 9. It is also divisible by 3 which is a factor of 9.
Can you say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m ?
Solution:
Yes, if a number is divisible by any number m, then it will also be divisible by each of the factors of m.
e.g., 42 is divisible by 21
Factors of 21 are 1, 3, 7
∴ 42 is also divisible by 1, 3, or 7.

Question 2.
(i) Write a 3-digit number abc as 100a + 10b + c
= 99a + 11b + (a – b + c)
= 11(9a + b) (a – b + c)
If the number abc is divisible by 11, then wliat can you say about (a – b + c) ?
Is it necessary that (a + c – b) she old be divisible by 11 ?
(ii) Write a 4-digit number abed us 1000a + 100b + 10c + d
= (1001a + 99b + 11c) – (a – b + c – d)
= 11(91a + 9b + c) + [(b + d) – (a + c)]
If the number abed is divisible by 11, then what can you say about [(b + d) – (a + c)]?
(iii) From (i) and (ii) above, can you say that a number will be divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is divisible by 11 ?
Solution:
(i) abc – 100a + 10b + c
= 100 × 1 + 10 × 2 + 1 [Here a = 1, b = 2 and c = 1]
= 99 × 1 + (11 × 2) + (1 – 2 + 1)
= 11(9 × 1 + 2) + (1 – 2 + 1)
It is clear from above example that the value of (a – b + c) must be zero if the number abc is divisible by 11.

(ii) Let the number be abcd = 9537. [Here a = 9, b = 5, c = 3 and d = 7]
9537 = 1000 × 9 + 100 × 5 + 10 × 3 + 7
= (1001 × 9 + 99 × 5 + 11 × 3) – (9 – 5 + 3 + 7)
= 11(91 × 9 + 9 × 5 + 3) + [(5 + 7) – (9 + 3)]
So, the value of [(b + d) – (a + c)] = 0 if abcd is divisible by 11.

(iii) Yes, it is true.

Try These (Page 260)

Question 1.
Check the divisibility of the following numbers by 3.
1. 108
2. 616
3. 294
4. 432
5. 927.
Solution:
(1) The sum of the digits of 108 is 1 + 0 + 8 = 9
∵ 9 is divisible by 3.
∴ 108 is divisible by 3 [If the sum of the digits is divisible by 3 then the number is also divisible by 3].

(2) The sum of the digits of 616 is 6 + 1 + 6
= 13
Since 13 is not divisible by 3.
Therefore, 616 is not divisible by 3.

(3) The sum of the digits of 294 is 2 + 9 + 4
= 15
∵ 15 is divisible by 3.
∴ The number 294 is divisible by 3.

(4) The sum of the digits 432 is 4 + 3 + 2 = 9.
∵ 9 is divisible by 3.
∴ 432 is divisible by 3.

(5) The sum of the digits of 927 is 9 + 2 + 7
= 18
∵ 18 is divisible by 3.
∴ 927 is divisible by 3.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers Ex 16.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 16 Playing with Numbers Exercise 16.2

Question 1.
If 21y5 is a multiple of 9, where y is: a digit, what is the value of y ?
Solution:
Since 21y5 is a multiple of 9.
i.e. 21y5 is divisible by 9.
Therefore, 2 + 1 + y + 5 = (8 + y) must be a multiple of 9. i.e. (8 + y) should be divisible by 9.
This is possible when 8 + y = 9 or 18
⇒ 8 + y = 9 or 8 + y = 18
y = 1 or y = 10
But, since x is a digit, therefore y = 10 is not possible.
Thus y = 1.

Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z ?
You will find that there are two answers for the last problem. Why is this so ?
Solution:
Since 31z5 is divisible by 9.
∴ 3 + 1 + z + 5 = a multiples of 9.
9 + z = 9, 18 or 27
⇒ 9 + z = 9 9 + z = 18
⇒ z = 0 z = 9
9 + z = 27
z = 21
which is not a one digit number.
∴ The values of z are (0 or 9).
There are two values of z as the sum of digits is a multiple of 9. So, it may be 9, 18, 27 … any one of them.

Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x ?
[Hint: Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers : 0, 3, 6, 9, 12, 15, 18, … . But since a: is a digit, it can only be that 6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.]
Solution:
We have 24x is a multiple of 3.
∴ 2 + 4 + x = 6 + x
is a multiple of 3.
∴ 6 + x = 0, 3, 6, 9, 12, 15, …
But, x is a digit.
∴ It can only be that
6 + x = 6 or 9, 12 or 15
∴ x = 0, 3, 6 or 9.

Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z ?
Solution:
Since 31z5 is a multiple of 3.
∴ The sum of the digits (3 + 1 + z + 5) is a multiple of 3.
So, 9 + z is one of these numbers :
0, 3, 6, 9, 12, …
9 + z = 9 ⇒ z = 1
[Values less than 9 gives negative result]
9 + z = 12 ⇒ z = 3
9 + 2= 15 ⇒ z = 6
9 + z = 18 ⇒ z = 9
9 + z = 21 ⇒ z = 12
which is not a one digit number.
∴ The values of z are 1, 3, 6 or 9.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers Ex 16.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 16 Playing with Numbers Exercise 16.1

Question 1.
Find the values of the letters in each of the following and give reasons for the steps involved.

Solution:
1. We have

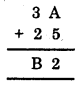
Study the addition in the ones column: from A + 5, we get ‘2’ that is, a number whose ones digit is 2.
Thus, A should be 7. So the puzzle can be solved as shown below :

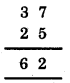
That is, B = 6.

2. We have

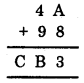
Here, A + 8 = 3 (a number whose ones digit is 3)
∴ ‘A’ should be 5.
Now,

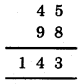
Thus, A = 5, B = 4 and C = 1.

3. We have

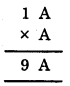
Since the ones digit of, A × A = A, so, it must be 6, because since produce of a number and A is 9.
i.e. 1 × A = 9 ⇒ A = 9
but A = 9 does not satisfies.
So, A = 6
Now,

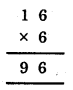
4. We have

Addition in ones column :
Here, B + 7 is A’ that is a number whose ones digit is ‘A’.
Let us put the values of ‘B’ starting from 0.
If B = 0, then A = 7 ∴ 7 + 6 ≠ 6
If B = 1, then A = 8 ∴ 8 + 3 ≠ 6
If B = 2, then A = 9 ∴ 9 + 3 ≠ 6
If B = 5, then A = 2 ∴ (2 + 3) + 1 = 6

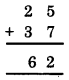
So, B = 5 and A = 2 satisfies the given condition.

5. We have

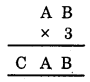
Since the ones digit of B × 3 is B, it must be B = 0 or B = 5.
Now look at A.

So, B = 0 and A = 5 and C = 1.

6. We have

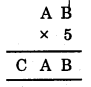
Since the ones digit of B × 5 is B
∴ B must be 0 or 5
Now, look at A.
Use hits and trial method :

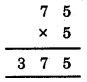
∴ A = 7, B = 5 and C = 3.

7. We have

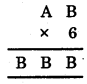
Since the ones digit of B × 6 is 6.
∴ Possible values of B are 0, 4, 6 and 8.
Now, look at A.
So, the value of BBB may be 444,666 or 888. [000 is not possible]
∴ 666 ÷ 6 = 111
which is a 3-digits number.
888 ÷ 6 = 148
which is a 3-digits number.
444 ÷ 6 = 74
which is a 2-digits number.

Thus, B = 4 and A = 7.

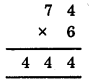
8. We have

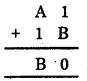
If you study the addition in the ones column i.e. (1 + B), you get ‘0’.
∴ B should be 9.
Thus, A must be 7.

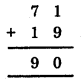
Thus, B = 9 and A = 7.

9. We have

If you study the addition in the ones column i.e. (B + 1) then you get ‘8’.
∴ ‘B’ should be 7 and A should be 4.

So, the given condition is satisfied.
Hence, B = 7 and A = 4.

10. We have

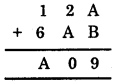
Since addition of ones column gives the value 9.
∴ A + B should be (1, 8) or (8, 1).
Now, let us apply hits and trial method.
If A = 1 and B = 8, then

If A = 8 and B = 1, then

Thus, A = 8 and B = 1 satisfies the given condition.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 15 Introduction to Graphs InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 15 Introduction to Graphs InText Questions

Try These (Page 244)

Question 1.
The following table gives the quantity of petrol and its cost:

Plot a graph to show the data.
Also, use the graph to find how much petrol can be purchased for Rs. 800.
Solution:
(i) Let us take a suitable scale on both the axes (Fig. 15.14).

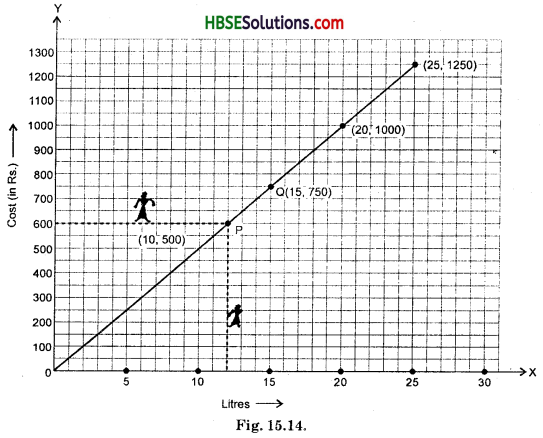
(ii) Mark number of litres along the horizontal axis.
(iii) Mark cost of petrol along the vertical axis.
(iv) Plot the points : (10, 500), (15, 750), (20, 1000), (25, 1250).
(v) Join the points.
If we observe that graph and drop perpendiculars from 800. The point is Q. We draw perpendicular from this point on X-axis. The required value is 16 litre.

Try These (Page 245)

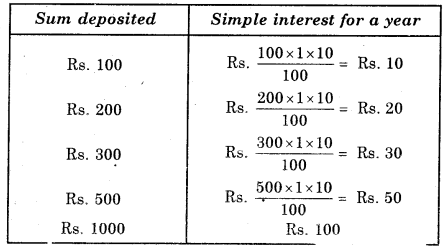
Question 1.
A bank gives 10% Simple Interest (S.I.) on deposits by senior citizens. Draw a graph to illustrate the relation between the sum deposited and simple interest earned. Find from your graph
(a) the annual interest obtainable for an investment of Rs. 250.
(b) the investment one has to make to get an annual simple interest of Rs. 70.
Is this, a case of direct variation ? Justify your answer.
Solution:

Steps to follow :
1. Find the quantities to be plotted as Deposit and S.I.
2. Decide the quantities to be taken on x-axis and on y-axis.
3. Choose a scale.
4. Plot points.
5. Join the points.
We get a table of values

(i) Scale : 1 unit = Rs. 100 on horizontal axis; 1 unit = Rs. 10 on vertical axis.
(ii) Mark Deposits along horizontal axis.
(iii) Mark Simple Interest along vertical axis.
(iv) Plot the points : (100, 10), (200, 20), (300, 30), (500, 50) etc.
(v) Join the points. We get a graph that is a line (Fig 15.15).

(a) Corresponding to Rs. 250 on horizontal axis, we get the interest to be Rs. 25 on the vertical axis.
(b) Corresponding to Rs. 70 on the vertical axis, we get the sum to be Rs. 700 on the horizontal axis.
Yes, this is a case of direct variation. More you deposit more you earn interest. Also, the graph is a straight line which indicates that the two quantities Simple Interest and amount deposited are in direct variation.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 15 Introduction to Graphs Ex 15.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 15 Introduction to Graphs Exercise 15.3

Question 1.
Draw the graphs for the following tables of values, with suitable scales on the axes.
(a) Cost of apples

(b) Distance travelled by a car

(i) How much distance did the car cover during the period 7.30 a.m. to 8 a.m. ?
(ii) What was the time when the car had covered a distance of 100 km since it’s start ?
(c) Interest on deposits for a year

(i) Does the graph pass through the origin ?
(ii) Use the graph to find the interest on Rs. 2500 for a year.
(iii) To get an interest of Rs. 280 per year, how much money should be deposited ?
Solution:
(a)

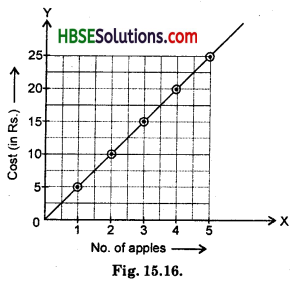
Scale : Horizontal: 1 unit = 1 apple
Vertical: 1 unit = Rs. 5
Here, 10 small division = 1 unit
Steps to follow :
(i) Mark no. of apples along horizontal axis.
(ii) Mark cost (in Rs.) along vertical axis.
(iii) Plot the points as shown in graph.
(iv) Join the points (1, 5), (2, 10), (3, 15), (4, 20) and (5, 25).

(b)


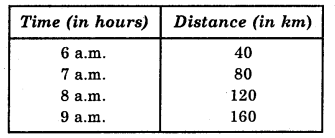
Scale : 2 units = 1 hour (Horizontal line)
1 unit = 40 km (Vertical line)
(i) Corresponding to 7.30 a.m. on horizontal axis, we get the distance 100 km on vertical axis.
So, distance covered by car during 7.30 a.m. and 8 a.m. = 120 – 100 = 20 km.
(ii) 7.30 a.m.

(c)

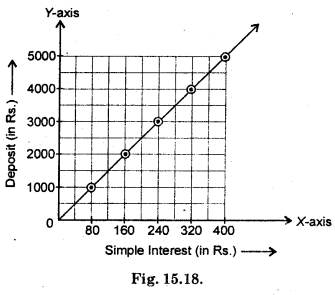
Scale :
Horizontal : 1 unit = Rs. 80
Vertical: 1 unit = Rs. 1000
Hence, 10 small division = 1 unit.
Steps Of follow :
(i) Mark simple interest (in Rs.) along horizontal axis.
(ii) Mark deposite (in Rs.) along vertical axis
(iii) Plot the points as showin in graph.
(iv) Joint the points (80, 1000), (160, 2000), (240, 3000), (320, 4000), (400, 5000)

Question 2.
Draw a graph for the following :
(i)

Is it a linear graph ?
(ii)

Is it a linear graph ?
Solution:

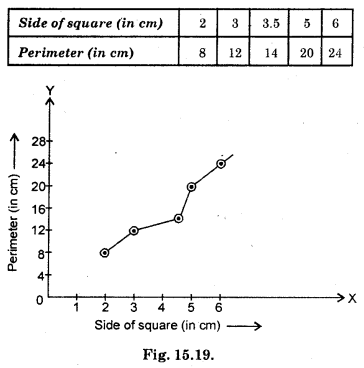
Scale : 1 unit on horizontal line = 1 cm
1 unit on vertical line = 4 cm
Since graph is not a straight line.
∴ It is not a linear graph.
(ii)

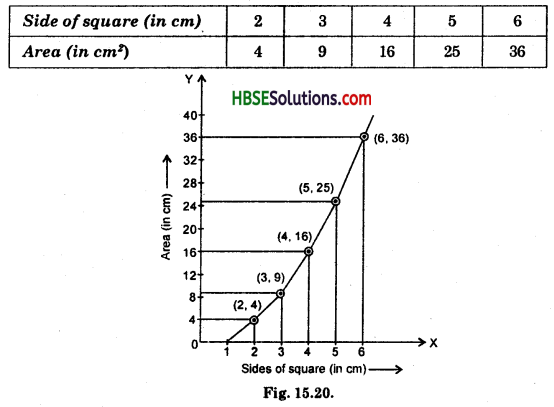
Scale : 1 unit on X-axis = 1 cm
1 unit on Y-axis = 4 cm²

Haryana State Board HBSE 8th Class Maths Solutions Chapter 15 Introduction to Graphs Ex 15.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 15 Introduction to Graphs Exercise 15.2

Question 1.
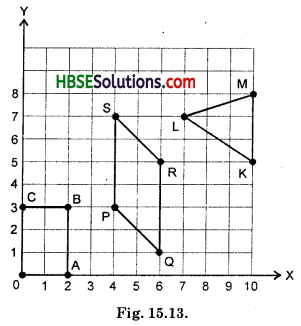
Plot the following points on a graph sheet. Verify if they lie on a line
(a) A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(b) P(1, 1), Q(2, 2), R(3, 3), S(4, 4)
(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5).
Solution:
(i) (a)

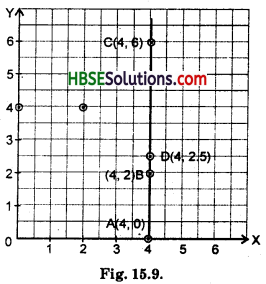
These points A, B, C and D lie on a line. The line is parallel to Y-axis.
(b)

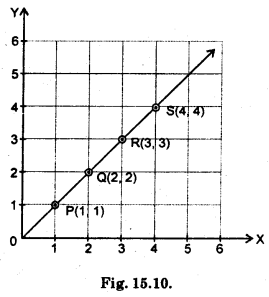
These points P, Q, R and S lie on a line. The line is a straight line passing through the origin.
(c)

These do not lie on a line. They form a rectangle.

Question 2.
Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and y-axis.
Solution:

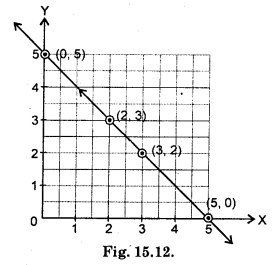
∴ Coordinates of the points at which this line meets the x-axis and y-axis are (5, 0) and (0, 5).

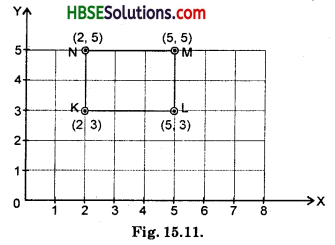
Question 3.
Write the coordinates of the vertices of each of these adjoining figures.

Solution:
Co-ordinates of the vertices of rectangle OABC are :
A(2, 0), B(2, 3), C(0, 3) and O(0, 0)
Coordinates of the vertices of parallelogram PQRS are :
P(4, 3), Q(6, 1), R(6, 5) and S(4, 7)
Coordinates of the vertices of △LMK are :
L(7, 7), M(10, 8) and K(10, 5).

Question 4.
State whether True or False. Correct that are false.
(i) A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
(ii) A point whose y-coordinate is zero and x-coordinate is 5 will lie on y-axis.
(iii) The coordinates of the origin are (0, 0).
Solution:
(i) True.
(ii) False. A point whose y-coordinate is zero and x-coordinate is 5 will lie on x-axis.
(iii) True.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 15 Introduction to Graphs Ex 15.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 15 Introduction to Graphs Exercise 15.1

Question 1.
The following graph shows the temperature of a patient in a hospital, recorded every hour.

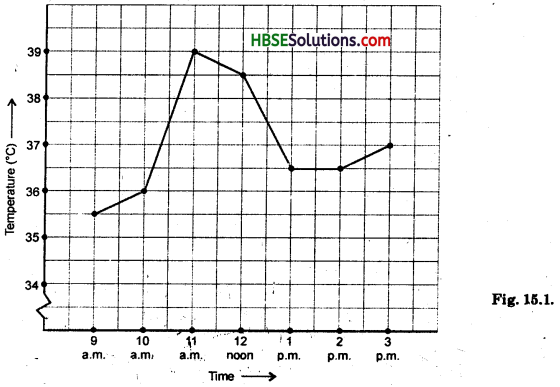
(a) What was the patient’s temperature at 1 p.m. ?
(b) When was the patient’s temperature 38.5°C ?
(c) The patient’s temperature was the same two times during the period given. What were these two times ?
(d) What was the temperature at 1.30 p.m. ? How did you arrive at your answer ?
(e) During which periods did the patients temperature showed an upward trend ?
Solution:
(a) The Patient’s temperature at 1 p.m. was 36.5°C.
(b) 12 noon.
(c) 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. was 36.5°. We observe the graph and finds that one fine indicates 30 minutes. So, taking a fine after 1 p.m. on X-axis move upward parallel to Y-axis where the line intersect the given line graph. It is obviously 36.5°C.
(e) 9 a.m. to 11 a.m.

Question 2.
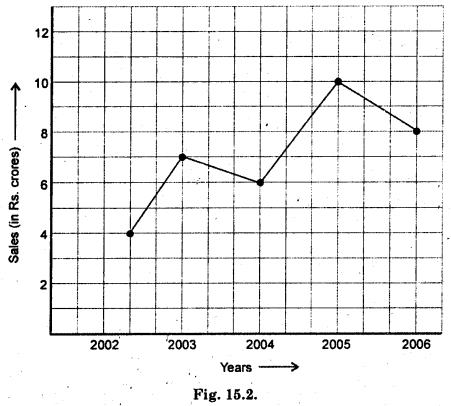
The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in (i) 2002 (ii) 2006 ?
(b) What were the sales in (i) 2003 (ii) 2005 ?
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year ?

Solution:
(a) (i) Sales in 2002 = 4 crores
(ii) Sales, in 2006 = 8 crores
(b) (i) Sales in 2003 = 7 crores
(ii) Sales in 2005 = 10 crores
(c) The difference between the sales in 2002 and 2006 = 8 – 4 = 4 crores.
(d) The greatest difference between the sales as compared to its previous year in 2004 – 2005.

Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

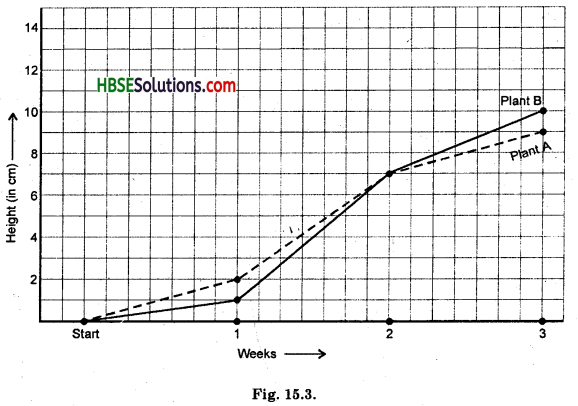
(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks ?
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks ?
(c) How much did Plant A grow during the 3rd week ?
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week ?
(e) During which week did Plant A grow most ?
(f) During which week did Plant B grow least ?
(g) Were the two plants of the same height during any week shown here ? Specify.
Solution:
(a) (i) Height of Plant A after 2 weeks = 7 cm
(ii) Height of Plant A after 3 weeks = 9 cm
(b) (i) Height of Plant B after 2 weeks = 7 cm
(ii) Height of Plant B after 3 weeks = 10 cm
(c) The Plant A grows during the 3rd week = 9 – 7 = 2 cm.
(d) The Plant B grows from the end of the 2nd week to the end of the 3rd week
= 10 cm – 7 cm = 3 cm.
(e) 2nd week.
(f) First week.
(g) Yes, the two plants have same height in the end of 2nd week.

Question 4.
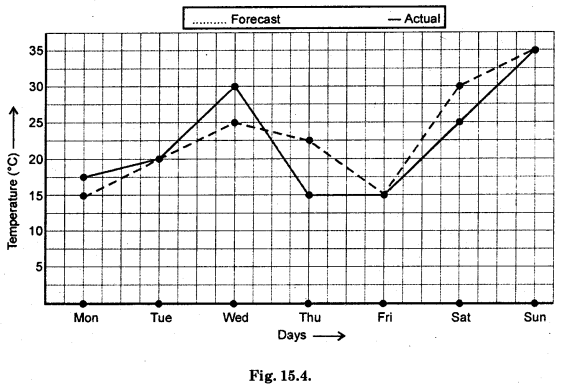
The following graph shows the temperature forecast and the actual temperature for each day of a week.
(a) On which days was the forecast temperature the same as the actual temperature ?
(b) What was the maximum forecast temperature during the week ?
(c) What was the minimum actual temperature during the week ?
(d) On which day did the actual temperature differ the most from the forecast temperature ?

Solution:
(a) Tuesday, Friday and Sunday.
(b) Sunday (35°C).
(c) 15°C.
(d) Thursday = 22.5°C – 15°C = 7.5°C.

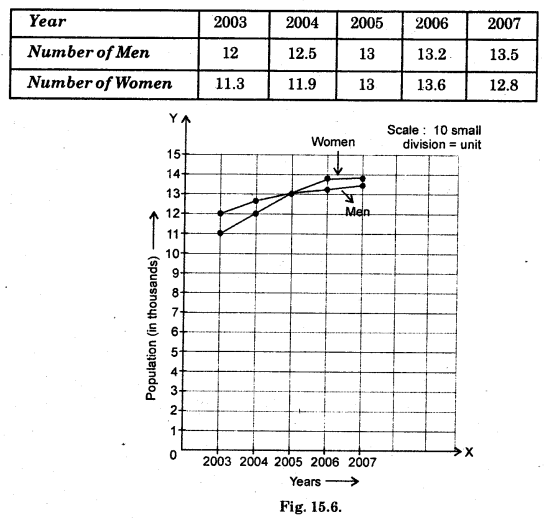
Question 5.
Use the tables below to draw linear graphs :
(a) The number of days a hill side city received snow in different years.

(b) Population (in thousands) of men and women in a village in different years.

Solution:
(a) Show fall received in different days during the years in a hill side city.


(b) Population in village (in thousands)

Question 6.
A courier-person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph :
(a) What is the scale taken for the time axis ?
(b) How much time did the person take for the travel ?
(c) How far is the place of the merchant from the town ?
(d) Did the person stop on his way ? Explain.
(e) During which period did he ride fastest ?

Solution:
(a) 4 small division = 1 hour
Let the 4 small division = 1 cm
∴ 1 cm = 1 hour
(b) 3 hour 30 minutes or 3.30 hour
(c) 22 km
(d) Yes, he stops between 10 a.m. to 10.30 a.m. because the distance is not changing with the change in time. In other words, we can say that the person is at rest. Hence, if a body remains at rest the graph of its motion is a straight line parallel to time-axis i.e. x-axis.
(e) Between 8 a.m. to 9 a.m.

Question 7.
Can there be a time-temperature graph as follows ? Justify your answer.


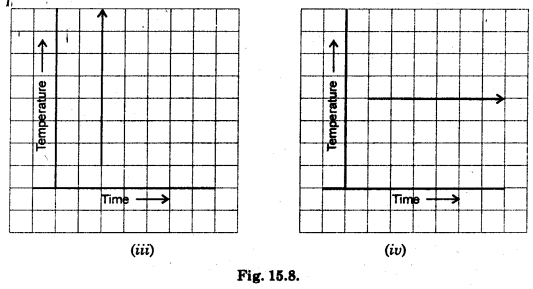
Solution:
(i) Yes, it may be a time-temperature graph because with change in time temperature may increase for example, during day time in summer.
(ii) Yes, it may be possible that with change in time temperature may fall uniformaly. For example, during night in winter.
(iii) No, it can not be a time-temperature graph. Here, temperature is changing without any change of time, which is impossible.
(iv) No, temperature cannot be constant with change in time. However, it may be possible for a short span of time.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 14 Factorization InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 14 Factorization InText Questions

Try These (Page 219)

Question 1.
Factorise :
(i) 12x + 36
(ii) 22y – 33z
(iii) 14 pq + 35 pqr
Solution:
(i) 12x + 36 = 12(x + 3)
(ii) 22y – 33z = 11 (2y + 3z)
(iii) 14 pq + 35pqr = 7pq (2 + 5r)

Try These (Page 225)

Question 1.
Divide:
(i) 24xy²z³ by 6yz²
(ii) 63a²b⁴c⁶ by 7a²b²c²
Solution:
(i) 24xy²z³ + 6yz²
= \(\frac{4 \times 6 \times x \times y \times y \times z \times z^{2}}{6 \times y \times z^{2}}\)
= 4 × x × y × z
= 4xyz

(ii) 63a²b⁴c⁶ ÷ 7a²b²c³
= \(\frac{7 \times 9 \times a^{2} \times b^{2} \times b^{2} \times c^{3} \times c^{2}}{7 \times a^{2} \times b^{2} \times c^{3}}\)
= 9 x b² x c³ = 9b²c³

Haryana State Board HBSE 8th Class Maths Solutions Chapter 14 Factorization Ex 14.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 14 Factorization Exercise 14.4

Find the correct the errors in the following matematical statements :
1. 4(x – 5) = 4x – 5
2. x(3x + 2) = 3x² + 2
3. 2x + 3y = 5xy
4. x + 2x + 3x = 5x
5. 5y + 2y + y – 7y = 0
6. 3x + 2x = 5x²
7. (2x)² + 4(2x) + 7 = 2x² + 8x + 7
8. (2x)² + 5x = 4x + 5x = 9x
9. (3x + 2)² = 3x² + 6x + 4
10. Substituting x = -3 in
(a ) x² + 5x + 4 gives (-3)² + 5(-3) + 4 =
9 + 2 + 4 = 15
(b) x² – 5x + 4 gives (-3)² – 5(-3) + 4 =
9 – 15 + 4 = -2
(c) x² + 5x gives (-3)² + 5(-3) = – 9 – 15 = -24
11. (y – 3)² = y² – 9
12. (z + 5)² = z² + 25
13. (2a + 3b) (a – b) = 2a² – 3b²
14. (a + 4) (a + 2) = a² + 8
15. (a – 4) (a – 2) = a² – 8
16. \(\frac{3 x^{2}}{3 x^{2}}\) = 0
17. \(\frac{3 x^{2}+1}{3 x^{2}}\) = 1 + 1 = 2
18. \(\frac{3 x}{3 x+2}\) = \(\frac{1}{2}\)
19. \(\frac{3}{4 x+3}\) = \(\frac{1}{4x}\)
20. \(\frac{4 x+5}{4 x}\) = 5
21. \(\frac{7 x+5}{5}\) = 7x.
Solution:
4(x – 5) = 4x – 5
L.H.S. = 4(x – 5)
= 4x – 20
Hence, 4(x – 5) = 4x – 20

2. x(3x + 2) = 3x² + 2
L.H.S. = x(3x + 2)
= 3x² + 2x .
Hence, x(3x + 2) = 3x² + 2x

3. 2x + 3y = 5x
L.H.S. = 2x + 3y
Hence, 2x + 3y = 2x + 3y or 3y + 2x

4. x + 2x + 3x = 5x
L.H.S. = x + 2x + 3x
= 6x
Hence, x + 2x + 3x = 6x

5. 5y + 2y + y – 7y = 0
L.H.S. = 5y + 2y + y – 7y
= 7y – 7y + y
= y
Hence, 5y + 2y + y – 7y = y

6. 3x + 2x = 5x²
L.H.S. = 3x + 2x = 5x
Hence, 3x + 2x = 5x

7. (2x)² + 4 (2x) + 7 = 2x² + 8x + 7
L.H.S: = (2x)² + 4 (2x) + 7
= 4x² + 8x + 7
Hence,
(2x)² + 4(2x) + 7 = 4x² + 8x + 7

8. (2x)² + (5x) = 4x + 5x = 9x
L.H.S. = (2x)² + (5x)
= 4x² + 5x
Hence, (2x)² + (5x) = 4x² + 5x

9. (3x + 2)² = 3x² + 6x + 4
L.H.S. = (3x + 2)²
= (3x)² + 2 × 3x × 2 + (2)²
[∵ (a + b)² = a² + 2ab + b²]
= 9x² + 12x + 4
Hence, (3x + 2)² = 9x² + 12x + 4

10 (a). If x = -3
x² + 5x + 4 gives (-3)² + 5 (-3) + 4
= 9 + 2 + 4 = 15
L.H.S. = x² + 5x + 4
= (-3)² + 5 × (-3) + 4
= 9 + (-15) + 4
= 13 – 15 = -2
Hence, x² + 5x + 4 = -2

(b) If x = -3
x² – 5x + 4 = (-3)² + 5 (-3) + 4
= 9 + 15 + 4 = 28

(c) If x = -3
x² + 5x = =(-3)² + 5(-3)
= 9 + (-15)
= 9 – 15 = -6

11. (y – 3)² = y² – 9
= y² – 2 × y × 3 + (3)²
[∵ (a – b)² = a² – 2ab + b²]
= y² – 6y + 9
Hence, (y – 3)² = y² – 6y + 9

12. (z + 5)² = z² + 25
L.H.S. = (z + 5)²
= (z)² + 2 × z × 5 + (5)²
= z² + 10z + 25
Hence, (z + 5)² = z² + 10z + 25

13. (2a + 3b) (a – b) = 2a² – 3b²
L.H.S. = (2a + 3b) (a – b)
= 2a² – 2ab + 3ab – 3b²
= 2a² – ab – 3b²
Hence, (2a + 3b) (a – b) = 2a² + ab – 3b².

14. (a + 4)(a + 2) = a² + 8
(a + 4)(a + 2) = a² + 8
L.H.S. = (a + 4)(a + 2)
= a² + 2a + 4a + 8
= a² + 6a + 8
Hence, (a + 4) (a + 2) = a² + 6a + 8

15. (a – 4)(a – 2) = a² – 8
L.H.S. = (a – 4)(a – 2)
= a² – 2a – 4a + 8
= a² – 6a + 8
Hence, (a – 4) (a – 2) = a² – 6a + 8.

16.

17.

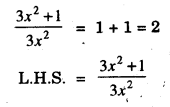
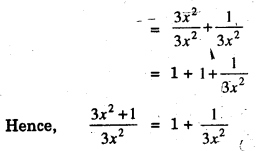
18.

19.

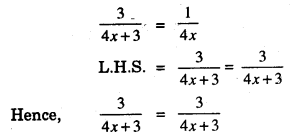
20.

21.