Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers InText Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 16 Playing with Numbers InText Questions
Try These (Page 250)
Question 1.
Write the following numbers in generalised form :
(i) 25
(ii) 73
(iii) 129
(iv) 302.
Solution:
(i) 25 = 2 × 10 + 5
[∵ ab = 10 × a + b where a and b are tens and ones place digits]
(ii) 73 = 7 × 10 + 3 ∵ ab = 10 × a + b]
(iii) 129 = 1 × 100 + 2 × 10 + 1 × 9
[∵ abc = 100 × a + 10 × b + 1 × c where a, b, c are hundreds, tens and ones place digits]
(iv) 302 = 100 × 3 + 0 × 10 + 1 × 2.
Question 2.
Write the following in the usual form :
(i) 10 × 5 + 6
(ii) 100 × 7 + 10 × 1 + 8
(iii) 100 × a + 10 × c + b.
Solution:
(i) 10 × 5 + 6 = 50 + 6 = 56
(ii) 100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718
(iii) 100 × a + 10 × c + b = 100a + 10c + b.
![]()
Try These (Page 251)
Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below :
1. 27
2. 39
3. 64
4. 17
Solution:

Conclusion : It is obvious from the above games with numbers that remainder is zero in each cases if we follow the procedure explained above. Quotient is always (a + b) i.e. 2 + 7 = 9 and so on.
Question 2.
Check what the result would have been if Sundaram had chosen the numbers shown below :
1. 17
2. 21
3. 96
4. 37.
Solution:

Hence, we observe that the quotient in each cases is either (a – b) or (b – a) according as a > b or a
![]()
Try These (Page 252)
Question 1.
Check what the result would have been if Minakshi had chosen the numbers shown below. In each case keep a record of the quotient obtained at the end.
1. 132
2. 469
3. 737
4. 901.
Solution:
1. Let the Minakshi had chosen the 3-digit number 132. So she got:
Reversed number : 231
Difference : 231 – 132 = 99
Division by 99 : 99 ÷ 99 = 1, with no remainder
Hence, Quotient = 1, Remainder = 0
2. Here,
Original number : 469
Difference : 964 – 469 = 495
Reversed number : 964
Division (by 99) : 495 ÷ 99 = 5
∴ Quotient = 5, Remainder = 0 (i.e. No remainder).
3. Here
Original number : 737
Reversed number : 737
Difference : 737 – 737 = 0
Division (by 99) : 0 ÷ 99 = 0 with no remainder
Hence, Quotient = 0, Remainder = 0
4. Here
Original number : 901
Reversed number : 109
Difference : 901 – 109 = 792
Division (by 99) : 792 ÷ 109 = 0 with no remainder
Hence, Quotient = 8, Remainder = 0
Conclusion : Hence, the resulting number is divisible by 99 in each cases and the quotient obtained is [(c – a) or (a – c)]. So, the remainder is zero.
Try These (Page 253)
Question 1.
Check what the result, would have been if Sundaram had chosen the numbers shown below :
1. 417
2. 632
3. 117
4. 937
Solution:
1. Original dumber
= 417 [It is in the form abc]
The number obtained by changing the digits like (cab)
= 741
and the other number in the form (bca) = 174
[Here, a = 4, b = 1 and c = 7]
Now add them up :
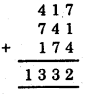
Then, we divide the resulting number 1332 by 37
∴ 1332 ÷ 37 = 36, with no remainder.
Hence, the number is divisible by 37 and remainder is 0.
2. Here, abc = 632
[∵ a = 6, b = 3 and c = 2]
cab = 263
and bca = 326
Add them up :
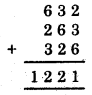
Divide the number by 37.
1221 ÷ 37 = 33, with no remainder.
∴ The number so obtained is divisible by 37.
Thus, Quotient = 33, Remainder = 0.
3. Here, abc =117
[Here a = 1, b = 1 and c = 7] c
ab = 711
and bca = 171
Add them up :
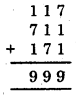
Divide the number by 37.
999 ÷ 37 = 27, with no remainder.
∴ The resulting number is divisible by 37.
Thus, Quotient = 27, Remainder = 0.
4. We have abc = 937
[Here a = 9, b = 3 and c = 7]
cab = 793
and bca = 379
Add them up:

Divide the number so obtained by 37.
2109 + 37 = 57, with no remainder.
∴ The resulting number is divisible by 37. Thus, Quotient = 57, Remainder = 0.
![]()
Try These (Page 255)
Question 1.
Write a 2-digit number ab and the number obtained by reversing its digits i.e., ba. Find their sum. Let the sum be a 3¬digit number dad
i.e. ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
(i) The sum a + b can not exceed 18 (why) ?
(ii) Is dad a multiple of 11 ?
(iii) Is dad less than 198 ?
(iv) Write all the 3-digit num bers which are multiples of 11 upto 198.
Find the values of a and d.
Solution:
Let a 2-diglt number be 87.
Then, the number obtained by reversing it will be 78.
Sum of these two numbers i.e. ab + ba = 87 + 78 = 165
165 is a 3-digit number.
Sum of digits = a + 6 = 8 + 7 = 15 which is less than 18.
(i) Take the maximum value of 2-digit number which is 99.
Even then, ab + ba = 99 + 99 = 198
So, a + b = \(\frac{198}{11}\) = 18
[∵ 11(a + b) = dad]
Thus, a + b can not exceed 18.
(ii) Yes, it is a multiple of 11.
(iii) Yes, it is less than 198.
(iv) 3-digits numbers which are multiples of 11 are :
11 × 10 = 110 Here, dad = 110, ∴ d = 1 or 0, a = 1
11 × 11 = 121; dad = 121 a = 2, d = 1
11 × 12 = 132; a = 3, d = 1 or 2
11 × 13 = 143; a = 4, d = 1 or 3
11 × 14 = 154; a = 4, d = 1 or 4
11 × 15 = 165; a = 6, d = 1 or 5
11 × 16 = 176; a = 7, d = 1 or 6
Try These (Page 257)
Question 1.
If the division N + 5 leaves a remainder of 3, what might be the ones digit of N ?
Answer:
The one’s digit, when divided by 5, must leave a remainder of 3. So the one’s digit must be either 3 or 8.
![]()
Question 2.
If the division N + 5 leaves a remainder of 1, what might be the one’s digit of N ?
Answer:
The one’s digit when divided by 5, must leave a remainder 1.
∴ The one’s digit must be either 1 or 6.
Question 3.
If the division N + 5 leaves a remainder of 4, what might be the one’s digit of N ?
Answer:
The one’s digit must be either 4 or 9.
For example,

![]()
Try These (Page 257-258)
Question 1.
If the division N + 2 leaves a remainder of 1, what might be the one’s digit of N ?
Answer:
N is odd; so ;its one’s digit is odd. Therefore, the one’s digit must be 1, 3, 5, 7 or 9.
Question 2.
If the division N + 2 leaves a remainder (t.e., zero remainder), what might be the one’s digit of N ?
Answer:
The one’s digit of N must be 0, 2, 4, 6 or 8 i.e. an even number.
![]()
Question 3.
Supose that the division N + 5 leaves a remainder of 4, and the division N + 2 leaves a remainder of 1. What must be the one’s digit of N ?
Answer:
∵ N ÷ 5 leaves a remainder 4.
∴ One’s digit of N should be 4 or 9.
Now, N ÷ 2 leaves a remainder of 1
∴ One’s digit of N are 1, 3, 5, 7, 9.
9 is a common digit in both the cases.
∴ One’s, digit of N must be 9.
Try These (Page 259)
Question 1.
Check the divisibility of the following numbers by 9 :
1. 108
2. 616
3. 294
4. 432
5. 927.
Solution:
(1) The sum of the digits of 108 is 1 + 0 + 8 = 9
So, this number is divisible by 9 because the sum of its digits is divisible by 9.
(2) The sum of the digits of 616 is 6 + 1 + 6 = 13
∵ 13 is not divisible by 9,
∴ Thus no. is also not divisible by 9.
(3) The sum of the digits of 294 is 2 + 9 + 4 = 15
∵ 15 is not divisible by 9.
∴ 294 is not divisible by 9.
(4) The sum of the digits 432 is 4 + 3 + 2 = 9.
∵ Sum of the digits i.e. 9 is divisible by 9.
∴ 432 is divisible by 9.
(5) The sum of the digits of 927 is 9 + 2 + 7 = 18
So, this number is divisible by 9 because sum of the digits i.e. 18 is divisible by 9.
![]()
Think, Discuss and Write (Page 259)
Question 1.
You have seen that a number 450 is divisible by 10. It is also divisible by 2 and 5 which are factors of 10. Similarly, a number 135 is divisible 9. It is also divisible by 3 which is a factor of 9.
Can you say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m ?
Solution:
Yes, if a number is divisible by any number m, then it will also be divisible by each of the factors of m.
e.g., 42 is divisible by 21
Factors of 21 are 1, 3, 7
∴ 42 is also divisible by 1, 3, or 7.
Question 2.
(i) Write a 3-digit number abc as 100a + 10b + c
= 99a + 11b + (a – b + c)
= 11(9a + b) (a – b + c)
If the number abc is divisible by 11, then wliat can you say about (a – b + c) ?
Is it necessary that (a + c – b) she old be divisible by 11 ?
(ii) Write a 4-digit number abed us 1000a + 100b + 10c + d
= (1001a + 99b + 11c) – (a – b + c – d)
= 11(91a + 9b + c) + [(b + d) – (a + c)]
If the number abed is divisible by 11, then what can you say about [(b + d) – (a + c)]?
(iii) From (i) and (ii) above, can you say that a number will be divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is divisible by 11 ?
Solution:
(i) abc – 100a + 10b + c
= 100 × 1 + 10 × 2 + 1 [Here a = 1, b = 2 and c = 1]
= 99 × 1 + (11 × 2) + (1 – 2 + 1)
= 11(9 × 1 + 2) + (1 – 2 + 1)
It is clear from above example that the value of (a – b + c) must be zero if the number abc is divisible by 11.
(ii) Let the number be abcd = 9537. [Here a = 9, b = 5, c = 3 and d = 7]
9537 = 1000 × 9 + 100 × 5 + 10 × 3 + 7
= (1001 × 9 + 99 × 5 + 11 × 3) – (9 – 5 + 3 + 7)
= 11(91 × 9 + 9 × 5 + 3) + [(5 + 7) – (9 + 3)]
So, the value of [(b + d) – (a + c)] = 0 if abcd is divisible by 11.
(iii) Yes, it is true.
![]()
Try These (Page 260)
Question 1.
Check the divisibility of the following numbers by 3.
1. 108
2. 616
3. 294
4. 432
5. 927.
Solution:
(1) The sum of the digits of 108 is 1 + 0 + 8 = 9
∵ 9 is divisible by 3.
∴ 108 is divisible by 3 [If the sum of the digits is divisible by 3 then the number is also divisible by 3].
(2) The sum of the digits of 616 is 6 + 1 + 6
= 13
Since 13 is not divisible by 3.
Therefore, 616 is not divisible by 3.
(3) The sum of the digits of 294 is 2 + 9 + 4
= 15
∵ 15 is divisible by 3.
∴ The number 294 is divisible by 3.
(4) The sum of the digits 432 is 4 + 3 + 2 = 9.
∵ 9 is divisible by 3.
∴ 432 is divisible by 3.
(5) The sum of the digits of 927 is 9 + 2 + 7
= 18
∵ 18 is divisible by 3.
∴ 927 is divisible by 3.