Class 8

Haryana State Board HBSE 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 3 Understanding Quadrilaterals InText Questions

Do This (Page 40-41)

Question 1.
Take any quadrilateral, say ABCD (in figure). Divide it into two triangles, by drawing a diagonal. You get six angles 1,2, 3, 4, 5 and 6.

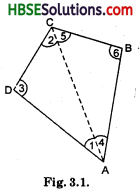
Use the angle-sum property of a triangle and argue how the sum of the measures of ∠A, ∠B, ∠C and ∠D amounts to 180°+ 180° = 360°.

Solution:
In △ACD
∠DAC + ∠ACD + ∠ADC = 180° (The angle sum property of a triangle)
or ∠1+ ∠2 + ∠3 = 180° …….(i)
In △ABC,
∠CAB + ∠ACB + ∠ABC = 180°
∠4 + ∠5 + ∠6 = 180° …….(ii)
Adding (i) and (ii) we get
(∠1 + ∠4) + (∠2 + ∠ 5) + ∠3 + ∠6 = 360°
or ∠DAB + ∠DCB + ∠ADC + ∠ABC = 360°
∴ ∠A + ∠B + ∠C + ∠D = 360°.

Question 2.
Take four congruent card-board copies of any quadrilateral ABQD, with angles as shown in Fig. 3.3(i). Arrange the copies as shown in the figure where angles ∠1, ∠2, ∠3, ∠4 meet At a point [Fig. 3.3(ii)]

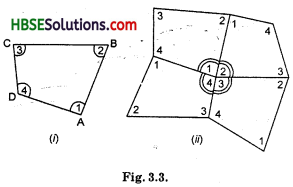
What can you say about the sum of the angles ∠1, ∠2, ∠3 and ∠4 ?
Solution:
The sum of the measures of the four angles of a quadrilateral is you may arrive at this result in several other ways also.
∠1 + ∠2 + ∠3 + ∠4 = 360°
The sum of the measures of the four angles of a quadrilateral is 360°.

Question 3.
As before consider quadrilateral ABCD in Fig. 3.4.

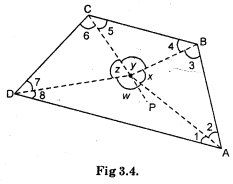
Let P be any point in its interior. Join P to vertices A, B, C and D. In the figure, consider △PAB. From this we see x = 180° – m∠2 – m∠3; similarly from △PBC, y = 180° – m∠4 – m∠5, from △SPCD, z = 180° – m∠6 – m∠7 and from △PDA, w = 180°- m∠8- m∠1. Use this to find the total measure m∠l + m∠2 + ………. + m∠8, does it help you to arrive at the result ?
Remember:
∠x + ∠y + ∠z + ∠W = 360°
Solution:
In △PAB, ∠x = 180° – m∠2 -m∠3 …(i)
[The angle-sum property of a triangle]
In △PBC, ∠y = 180° — m∠4 – m∠5 ….(ii)
In △PCD, ∠z = 180° – m∠6 – m∠7 …(iü)

Question 4.
These quadrilaterals were convex. What would happen if the quadrilateral is not convex ? Consider quadrilateral ABCD. Split it into two triangles and find the sum of the interior angles.

Solution:
In △ABD,
∠ABD + ∠ADB + ∠BAD = 180° …(i)
In △BDC,
∠BDC + ∠DBC + ∠BCD = 180° …(ii)
Adding (i) and (ii)
(∠ABD + ∠DBC) + (∠ADB + ∠CBD) + (∠DAB + ∠DCB) = 360°
∠ABC + ∠ADC + ∠DAB + ∠DCB = 360°.

Try These (Page 43)

Take a regular hexagon Fig. 3.12.

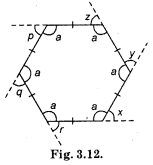
Question 1.
What is the sum of the measures of its exterior angles x, y, z, p q, r ?
Solution:
(∠a + ∠r) + (∠a + ∠x) + (∠a + ∠y) + (∠a + ∠z) + (∠a + ∠p) + (∠a + ∠q) = 6 × 180°
[∵ ∠a + ∠r, ∠a + ∠x ……. (∠a + ∠q formed linear pair]
or ∠a + ∠a + ∠a + ∠a + ∠a + ∠a + (∠r + ∠x + ∠y + ∠z + ∠p + ∠q) = 1080°
or 6∠a + 360° = 1080°
[Sum of exterior angles of a polygon]
or 6∠a = 1080-360°
= 720°
∴ ∠a = \(\frac{720}{6}\) = 120°
Therefore sum of its exterior angle
=∠q + ∠r + ∠x + ∠y + ∠z + ∠p
=(180 – 120) × 6
= 360°.

Question 2.
Is x = y = z = p = q = r ? Why ?
Solution:
Yes, ∠a = 120°
∴ ∠a + ∠r =∠a + ∠x = ∠a + ∠y
= ∠a + ∠z = ∠a + ∠p
= ∠a + ∠q [Linear pair]
But ∠a = 120°
∴ ∠r = ∠x = ∠y
= ∠z = ∠p = ∠q
= 180 – 120° = 60°.

Question 3.
What is the measure of each ?
(i) Exterior angle
(ii) Interior angle.
Solution:
(i) The measure of each exterior angle = \(\frac{360}{6}\) = 60°
(ii) The measure of each interior angle = a + 60° = 180°
∴ a = 120°.

Question 4.
Repeat this activity for the cases of
(i) a regular octagon
(ii) a regular 20-gon
Solution:
The exterior angle of a regular octagon
= \(\frac{360}{8}\) = 45°
The exterior angle of a regular 20-gon
= \(\frac{360}{20}\) = 18°
The interior angle of a regular octagon
= 180° – 45° = 135°
The interior angle of a regular 20-gon
= 180° – 18° = 162°.

Try These (Page 43)

Question 1.
Take two identical set squares with angles 30° – 60° – 90° and place them adjacently to form a parallelogram as shewn in Fig. 3.20. Does this help you to verify the above property?

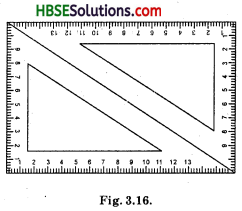
Solution:
we know that a parallelogram is a quadrilateral whose opposite sides are parallel.
From figure,
∠D = 60° + 30° = 90°
∠A = 90°
∠C = 90°
Similarly, ∠B = 30° + 60° = 90°
From figure \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are opposite sides and \(\overline{\mathrm{AD}}\) and \(\overline{\mathrm{BC}}\) are another opposite side.
∠A and ∠C are a pair of opposite angles.
∠B and ∠C are another pair of opposite angles.
\(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BC}}\) are adjacent sides. This means, one of the sides starts when the other sides.
Similarly, \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{CD}}\) are adjacent sides.
Thus, the property of the parallelogram opposite sides are equal and parallel knd their opposite angles are equal.
Hence, this figure is parallelogram or rectangle and verified.

Try These (Page 48)

Question 1.
Take two identical 30° – 60° – 90° set-squares and form a parallelogram as before. Does the figure obtained help you to confirm the above property?
Solution:
From figure
∠1 = ∠2 + 30° = alternate angle
∠3 = ∠4 = 60° alternate angle
Hence ∠B = ∠D = 90°
When AB and CD are parallel then its angles ∠1 and ∠2 are alternate angles and mutually equal.
or, if alternate angles are equal then opposite side AB and CD are parallel.
According to property of parallelogram opposite sides and opposite angles are equal.
Hence, ∠A = ∠C = 90° and ∠B = ∠D = 90°
and AB = CD andBC = AD.
Hence this is verified.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.6 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.6

Solve the following equations

Question 1.
\(\frac{8 x-3}{3 x}\) = 2
Solution:
\(\frac{8 x-3}{3 x}\) = 2
or, \(\frac{8 x-3}{3 x}\) 3x = 2 3x
or, 8x – 3 = 6x
or, 8x – 6x = 3
or, 2x = 3
or, x = \(\frac{3}{2}\)
∴ x = \(\frac{3}{2}\)

Question 2.
\(\frac{9 x}{7-6 x}\) = 15
Solution:
\(\frac{9 x}{7-6 x}\) = 15
or, \(\frac{9 x}{7-6 x}\) = 15
or, 15(7 – 6x) = 9x
or, 105 – 90x = 9x
or, 105 = 9x – 90x
or, 99x = 105
or, x = \(\frac{105}{99}\) = \(\frac{35}{33}\)
∴ x = \(\frac{35}{33}\)

Question 3.
\(\frac{z}{z+15}\) = \(\frac{4}{9}\)
Solution:
\(\frac{z}{z+15}\) = \(\frac{4}{9}\)
or, 9z = 4(z + 15)
or, 9z = 4z + 60
or, 9z – 4z = 60
or, 5z = 60
or, z = 12
∴ z = 12

Question 4.
\(\frac{3y+4}{2-6y}\) = \(\frac{-2}{5}\)
Solution:
\(\frac{3y+4}{2-6y}\) = \(\frac{-2}{5}\)
or, 5(3y + 4) = -2(2 – 6y)
or, 15y + 20 = -4 + 12y
or, 15y – 12y = -4 – 20
or, 3y = -24
or, y = \(\frac{-24}{3}\) = -8
∴ y = -8

Question 5.
\(\frac{7y+4}{y+2}\) = \(\frac{-4}{3}\)
Solution:
\(\frac{7y+4}{y+2}\) = \(\frac{-4}{3}\)
or, 3(7y + 14) = -4(y + 2)
or, 21y + 12 = -4y – 8
or, 21y + 4y = -8 – 12
or, 25y = -20
or, y = \(-\frac{20}{25}\) = \(-\frac{4}{5}\)
∴ y = \(-\frac{4}{5}\)

Question 6.
The ages of Hari and Harry are in the ratio 5 : 7. Four years from now the ratio of their ages will be 3 : 4. Find their present ages.
Solution:
Let Hari’s present age be 5x
Harry present age be 7x
After four years Hari’s age = (5x + 4) years
After four years Harry’s age = (7x + 4) years
According to the question
Therefore \(\frac{5x+4}{7x+4}\) = \(\frac{3}{4}\)
or, 4 (5x + A) = 3 (7x + 4)
or, 20x + 16 = 21x + 12
or, 20x – 21x = 12 – 16
or, -x = -4
or, x = 4
∴ Hari’s present age = 5 × 4 = 20 years.
Harry’s present age = 7 × 4 = 28 years.

Question 7.
The denominator of a rational number is greater than its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the numberobtained is \(\frac{3}{2}\). Find the rational number.
Solution:
Let the numerator of a fraction be x
Denominator = x + 8
Fraction = \(\frac{x}{x+8}\)
2nd part of the question
Numerator = x + 17
Denominator = x + 8 – 1 = x + 7
Fraction = \(\frac{x+17}{x+7}\)
or, \(\frac{3}{2}\) = \(\frac{x+17}{x+7}\)
or, 3 (\(\frac{3}{4}\) + 7) = 2 (x + 17)
or, 3x + 21 = 2x + 34
or, 3x – 2x = 34 – 21
or, x = 13
(∴ denominator = 13 + 8 = 21)
∴ Fraction = \(\frac{13}{21}\)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.5 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.5

Solve the following linear equations

Question 1.
\(\frac{x}{2}-\frac{1}{5}\) = \(\frac{x}{3}+\frac{1}{4}\)
Solution:

Question 2.
\(\frac{n}{2}\) – \(\frac{3n}{4}\) + \(\frac{5n}{6}\) = 21
Solution:

Question 3.
x + 7 – \(\frac{8x}{3}\) = \(\frac{17}{6}\) – \(\frac{5x}{2}\)
Solution:

Question 4.
\(\frac{x-5}{3}\) = \(\frac{x-3}{5}\)
Solution:
\(\frac{x-5}{3}\) = \(\frac{x-3}{5}\)
or, 5(x – 5) = 3 (x – 3)
or, 5x – 25 = 3x – 9
or, 5x – 3x = -9 + 25
or, 2x = 16
or, x = \(\frac{16}{2}\)
∴ x = 8

Question 5.
\(\frac{3t-2}{4}\) – \(\frac{2t-3}{3}\) = \(\frac{2}{3}\) – t
Solution:

or, 3 (13t – 18) = 24
or, 39t – 54 = 24
or, 39t = 24 + 54 = 78
or, 39t = 78
or, t = 2

Question 6.
m – \(\frac{m-1}{2}\) = 1 – \(\frac{m-2}{3}\)
Solution:

or, 5m – 1 = 6
or, 5m = 6 + 1
or, 5m = 7
∴ m = \(\frac{7}{5}\)

Simplify and solve the following linear equations:

Question 7.
3 (t – 3) = 5 (2t + 1)
Solution:
3 (t – 3) = 5 (2t + 1)
or, 3t – 9 = 10t + 5
or, 3t – 10t = 5 + 9
or, -7t = 14
or, t = \(-\frac{14}{7}\) =-2
t = -2

Question 8.
15(y – 4) – 2(y – 9) + 5(y + 6) = 0
Solution:
15(y – 4) – 2(y – 9) + 5(y + 6) = 0
or, 15y – 60 – 2y + 18 + 5y + 30 = 0
or, 20y – 2y – 60 + 48 = 0
or, 18y – 12 = 0
or, 18y = 12
or, y = \(\frac{12}{18}\) = \(\frac{2}{3}\)
∴ y = \(\frac{2}{3}\)

Question 9.
3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
Solution:
3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
or, 15z – 21 – 18z + 22 = 32z – 52 – 17
or, 15z – 18z – 32z = -52 – 17 + 21 – 22
or, 15z – 50z = 21 – 91
or, -35z = -70
or, 35z = 70
or, z = 2
∴ z = 2

Question 10.
0.25 (4f – 3) = 0.05 (10f – 9)
Solution:
0.25 (4f – 3) = 0.05 (10f – 9)
or, f – 0.75 = 0.5f – 0.45
or, f – 0.5f = -0.45 + 0.75
or, 0.5f = 0.3
f = \(\frac{0.3}{0.5}\) = \(\frac{3}{5}\) = 0.6
∴ f = 0.6

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.4

Question 1.
Amina thinks of a number and subtracts \(\frac{5}{2}\) from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number?
Solution:
Let Amina thinks the number be x.
She subtracts \(\frac{5}{2}\) from x.
∴ Now, the result will be x – \(\frac{5}{2}\)
The result is multiply by 8
Therefore, (x – \(\frac{5}{2}\)) × 8 = 8x – 20
This number is three times the same number, therefore
8x – 20 = 3x
or, 8x – 3x = 20
or, 5x = 20
or, x = 4
∴ The number will be 4.

Question 2.
A positive number is 5 times another number. If 21 is added to both the numbers, then one of the new numbers becomes twice the other new number. What are the numbers?
Solution:
Let the another number be x.
The first number is 5x
21 is added to both the numbers then one of the new numbers becomes twice the other new number.
∴ 2(x + 21) = 5x + 21
or, 2x + 42 = 5x + 21
or, 2x – 5x = 21 – 42
or, -3x = -21
∴ x = 7
Other number = 7 × 5 = 35.
∴ The numbers are 7, 35.

Question 3.
Sum of the digits of a two-digit number is 9. When we interchange the digits, it is found that the resulting new number is greater than the original number by 27. What is the two digit number ?
Solution:
Let the ones place the number be x.
∴ Ten’s place = 9 – x
The number will be = 10 (9 – x) + x
(Two digit number = 10, tens place + one’s place)
After interchanging the digit we get 10x + 9 – x
This number is 27 more than original number
According to the question
10x + 9 – x = 10 (9 – x) + x + 27
or, 9x + 9 = 90 – 10x + x + 27
or, 9x = 117 – 9x – 9
or, 9x + 9x = 108
or, 18x = 108
or x = \(\frac{108}{18}\) = 6
∴ Ten’s place = 9 – 6 = 3
∴ The number will be = 10 × 3 + 6 = 36

Question 4.
One of the two digits of a two digit number is three times the other digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get 88. What is the original number ?
Solution:
Let one’s place of a two digit number be x
Ten’s place = 3x
The number will be 10.3x + x
After interchanging the digits we get
10x + 3x
According to the question,
10.3x + x + 10x + 3x = 88
or, 30x + x + 10x + 3x = 88
or, 44× = 88
or, x = 2
The original number = 10 × 3 × 2 + 2 = 62
[Note : According to the question, If you let one’s place is 3 times of ten’s place digit, the answer will be 26.]

Question 5.
Shobo’s mother’s present age is six times Shobo’s present age. Shobo’s age five years from now will be one third of his mother’s present age. What are their present ages?
Solution:
Let Shobo’s present age be x years.
Shobo’s mother’s present age 6x years
5 years after Shobo’s age = x + 5 years
According to the question
x + 5 = \(\frac{6x}{3}\)
or, x + 5 = 2x
or, 2x – x = 5
or, x = 5
∴ Shobo’s present age = 5 year’s
Shobo’s mother’s present age
= 6 × 5 = 30 years.

Question 6.
There is a narrow rectangular plot reserved for a school, in Mahuli village. The length and breadth of the plot are in the ratio 11:4. At the rate Rs. 100 per metre it will cost the village panchayat Rs. 75000 to fence the plot. What are the dimensions of the plot?
Solution:
Let the ratio be x
Length = llx and breadth = 4x
Rs. 100 cost 1 metre to fence the plot.
Rs. 7500 cost \(\frac{1}{100}\) × 75000 metre to fence the plot = 750 metre
∴ Perimeter of the plot
= 750 m
2 (11x + 4x) = 750
[∵ Perimeter -2(l + b)]
2 × 15x = 750
or, 30x = 750
or, x = 25
Therefore length = 11 × 25 = 275 m
breadth = 4 × 25 = 100 m

Question 7.
Hasan buys two kinds of cloth materials for school uniforms, shirt material that costs him Rs. 50 per metre and trouser material that costs him Rs. 90 per metre. For every 2 metres of the trouser material he buys 3 metres of the shirt material. He sells the materials at 12% and 10% profit respectively. His total sale is Rs. 36,660. How much trouser material did he buy?
Solution:
Hasan bpys shirt and trouser in ratio 2 : 3
Let the ratio be x
He buys 2x m of the trouser and 3cc m of the shirt material
The cost of the shirt material
= Rs. 3x × 50 = Rs. 150x
The cost of the trouser meterial =Rs. 2x × 90 = Rs. 180x
The S.P of the shirt material
= Rs. 150x + 12% of 150x
= 150x + \(\frac{12}{100}\) × 150x = Rs. 168x
The S.P of the trouser material
= Rs. 180x + 10% of 180x
= 180x + \(\frac{10}{100}\) × 180x = 198x
According to, the question,
168x + 198x = 36,660
or, 366x = 36,660
or, x = \(\frac{36,660}{366}\) = 100.16
Then trouser material is bought by him = 200 m.

Question 8.
Half of a herd of deer are grazing in the field and three fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Solution:
Let the number of deer in the herd be x
Number of deer who grazing in the field
= \(\frac{1}{2}\) of x = \(\frac{x}{2}\)
Rest Number of deer
= x – \(\frac{x}{2}\) = \(\frac{x}{2}\)
Three fourths of the remaining
= \(\frac{3}{4}\) of \(\frac{x}{2}\) = \(\frac{3x}{8}\)
Rest = \(\frac{x}{2}\) – \(\frac{3x}{8}\)
9 = \(\frac{4x-3x}{8}\)
or, 9 = \(\frac{x}{8}\)
∴ x = 9 × 8 = 72
2nd Method
Total number of deer in the herd = x
Hints :
∴ x = \(\frac{x}{2}\) + \(\frac{3x}{8}\) + 9
= \(\frac{4x+3x+72}{8}\)
∴ x = \(\frac{7x+72}{8}\)
8x = 7x + 72
8x – 7x = 72
x = 72

Question 9.
A grandfather is ten times older than his granddaughter. He is also 54 years older than her. Find their present ages.
Solution:
Let the present age of granddaughter be x years
The present age of grandfather = 10x years
According to the question
10x – x = 54
or, 9x = 54
∴ x = 6
∴ The present age of granddaughter = 6 years
The present age of grandfather = 10 × 6 years = 60 years

Question 10.
A man’s age is three times his son’s age. Ten years ago he was five times his son’s age. Find their present ages.
Solution:
Let the son’s present age be x years
Father’s present age = 3x years
Ten years ago son’s age = x – 10 years
Ten years ago father’s age = 3x – 10 years
According to the question
3x – 10 = 5 (x – 10)
or, 3x – 10 = 5x – 50
or, 3x – 5x = -50 + 10
or, -2x = -40
∴ x = 20
Therefore, Son’s present age = 20 years.
Father’s present age = 3 x 20 = 60 years.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.3

Solve the following equations and check your results :
Question 1.
3x = 2x + 18
Solution:
3x = 2x + 18
or, 3x – 2x = 18
∴ x = 18.
Check:
L.H.S. = 3 × 18 = 54
R.H.S. = 2 × 18 + 18 = 54
∴ L.H.S. = R.H.S.

Question 2.
5t – 3 = 3t – 5
Solution:
5t – 3 = 3t – 5
or, 5t – 3t = -5 + 3
or, 2t = -2
or, t = -1
∴ t = -1
Check:
L.H.S = 5(-1) – 3
= -5 – 3 = -8
R.H.S = 3(-1) – 5
= -3 – 5 = -8
∴ L.H.S = R.H.S

Question 3.
5x + 9 = 5 + 3x
Solution:
5x + 9 = 5 + 3x
or, 5x – 3x = 5 – 9
or, 2x = -4
or, x = -2
∴ x = -2
Check:
L.H.S. = 5 (-2) + 9
= – 10 + 9 = -1
R.H.S. = 5 +3 (-2)
= 5 – 6 = -1
∴ L.H.S. = R.H.S.

Question 4.
4z + 3 = 6 + 2z
Solution:
4z – 2z = 6 – 3
or, 2z = 3
or, z = \(\frac{3}{2}\)
Check:
L.H.S. = 4z + 3
= 4 × \(\frac{3}{2}\) + 3 = 9
R.H.S. = 6 + 2 × \(\frac{3}{2}\) = 9
∴ L.H.S. = R.H.S.

Question 5.
2x – 1 = 14 – x
Solution:
2x – 1 = 14 – x
or, 2x + x = 14 + 1
or, 3x = 15
or, x = 5
∴ x = 5
Check:
L.H.S. = 2 × 5 – 1
= 10 – 1 = 9
R.H.S. = 14 – 5 = 9
∴ L.H.S. = R.H.S.

Question 6.
8x + 4 = 3 (x – 1) + 7
Solution:
8x + 4 = 3 (x – 1) + 7
or, 8x + 4 = 3x – 3 + 7
or, 8x – 3x = -3 + 7 – 4
or, 5x = 0
∴ x = 0
Check:
L.H.S. = 8 × 0 + 4 = 4
R.H.S. = 3(0 – 1) + 7
= -3 + 7 = 4
∴ L.H.S. = R.H.S.

Question 7.
x = \(\frac{4}{5}\)(x + 10)
Solution:
x = \(\frac{4}{5}\)(x + 10)
or, 5x = 4(x + 10)
or, 5x = 4x + 40
or, 5x – 4x =40
∴ x = 40
Check:
L.H.S. = 40
R.H.S. = \(\frac{4}{5}\)(40 + 10)
= \(\frac{4}{5}\) × 50 = 40
∴ L.H.S. = R.H.S.

Question 8.
\(\frac{2x}{3}\) + 1 = \(\frac{7x}{15}\) + 3
Solution:

Question 9.
2y + \(\frac{5}{3}\) = \(\frac{26}{3}\) – y.
Solution:
2y + \(\frac{5}{3}\) = \(\frac{26}{3}\) – y
or, 2y + y = \(\frac{26}{3}\) – \(\frac{5}{3}\)
or, 3y = \(\frac{26-5}{3}\) = \(\frac{21}{3}\)
or, 3y = 7
∴ y = \(\frac{7}{3}\)

Question 10.
3m = 5m – \(\frac{8}{5}\)
Solution:
3m = 5m – \(\frac{-8}{5}\)
or, 3m – 5m = \(\frac{-8}{5}\)
or, -2m =\(\frac{-8}{5}\)
or, 2m = \(\frac{8}{5}\)
∴ m = \(\frac{8}{5 \times 2}\) = \(\frac{4}{5}\)
Check:
L.H.S = 3 × \(\frac{4}{5}\) = \(\frac{12}{5}\)
R.H.S = 5 × \(\frac{4}{5}\) – \(\frac{8}{5}\)
= 4 – \(\frac{8}{5}\) = \(\frac{12}{5}\)
∴ L.H.S = R.H.S

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.2

Question 1.
If you subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), you get \(\frac{1}{8}\). What is the number ?
Solution:
Let, the number be x.
Subtract \(\frac{1}{2}\) from x and multiply the,result by \(\frac{1}{2}\).
∴ (x – \(\frac{1}{2}\)) × \(\frac{1}{2}\) = \(\frac{1}{8}\)

Question 2.
The perimeter of a rectangular swimming pool is 154 m. Its length is 2m more than twice its breadth. What are the length and the breadth of the pool ?
Solution:
Let the breadth of swimming pool be x
∴ Length = 2x + 2
The perimeter of swimming pool = 154 m.
or, 2(l + b) = 154
or, 2 (2x + 2 + x) = 154
or, 2 (3x + 2) = 154
or, 6x + 4 = 154
or, 6x = 154 – 4
or, 6x = 150
x = \(\frac{150}{6}\) = 25
∴ Breadth = 25 m.
Length = 2 × 25 + 2 = 52 m.

Question 3.
The base of an isosceles triangle is \(\frac{4}{3}\) cm. The perimeter of the triangle is 4\(\frac{2}{15}\) cm. What is the length of either of the remaining equal sides?
Solution:
Let the length of one equal side be x.

According to the question
AB + BC + AC = 4\(\frac{2}{15}\) cm
x + \(\frac{4}{3}\) + x = \(\frac{62}{15}\)
⇒ 2x = \(\frac{62}{15}\) – \(\frac{4}{3}\) = \(\frac{42}{15}\)
∴ x = \(\frac{4}{3}\) = \(\frac{21}{15}\)
= \(\frac{7}{5}\) = 1\(\frac{2}{5}\) cm

Question 4.
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:
Let other number be x.
First number will be x + 15
Sum of two numbers is 95
or, x + x + 15 = 95
or, 2x + 15 = 95
or, 2x = 95 – 15 = 80
x = \(\frac{80}{2}\) = 40
∴ Other number = 40
One number = 40 + 15 = 55

Question 5.
Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers ?
Solution:
Let the ratio be x. The numbers will be 5x and 3x
According to the question
5x – 3x = 18
⇒ 2x = 18
x = 9
∴ 5x = 5 × 9 = 45
3x = 3 × 9 = 27
The numbers are 45, 27
2nd Method
Let the numbers are x and y
∴ \(\frac{x}{y}\) = \(\frac{5}{3}\)
3x = 5y ⇒ x = \(\frac{5y}{3}\) ………(i)
2nd part of the question
x – y = 18
From (i)
\(\frac{5y}{3}\) – y = 18
\(\frac{5y-3y}{3}\) = 18
\(\frac{2y}{3}\) = 18
2y = 18 × 3 = 54
y = 27
From (i) x = \(\frac{5×27}{3}\) = 45
∴ Numbers are 45, 27

Question 6.
Three consecutive integers add up to 51. What are these integers ?
Solution:
Let first integer be x
Second integer be x + 1
Third integer be x + 1 + 1 = x + 2 (The differ from two consecutive integers is 1.)
According to the question
x + x + 1 + x + 2 = 51
⇒ 3x + 3 = 51
⇒ 3x = 51 – 3 = 48
x = 16
∴ First integer = 16
Second integer = 17
Third integer = 18

Question 7.
The sum of three consecutive multiples of 8 is 888. Find the multiples.
Solution:
Let the first multiple of 8 be 8x:
Second multiple be 8x + 8
Third multiple be 8x + 8 + 8 = 8x + 16
According to the question
8x + 8x + 8 + 8x + 16= 888
or, 24x + 24 = 888
or, 24x = 888 – 24
or, 24x = 864
x = \(\frac{864}{24}\) = 36
∴ 8x = 8 × 36 = 288
8x + 8 = 288 + 8 = 296
8x + 16 = 288 + 16 = 304
∴ The numbes will be 288, 296 and 304.

Question 8.
Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74. Find these numbers.
Solution:
Let the first number be x
The second number = x + 1
The third number = x + 1 + 1 = x + 2
According to the question
2x + 3 (x + 1) + 4 (x + 2) – 74
or, 2x + 3x + 3 + 4x + 8 = 74
or, 9x + 11 = 74
or, 9x = 74 – 11 = 63
∴ x = \(\frac{36}{9}\) = 7
∴ The first number = 7
Second number = 7 + 1 = 8
Third number = 7 + 2 = 9

Question 9.
The ages of Rahul and Ilaroon are in the ratio 5 : 7. Four years later the sum of their ages will be 56 years. What are their present ages?
Solution:
Let the ratio be x
Rahul’s present age = 5x years
Haroon’s present age = 7x years
Four years later Rahul’s age will be 5x + 4 years
Four years later Haroon’s age will be 7x + 4 years
According to the question
5x + 4 + 7x + 4 = 56
12x + 8 = 56
or, 12x = 56 – 8 = 48
x = \(\frac{48}{12}\) = 4
∴ Rahul’s present age = 5 × 4 = 20 years
Haroon’s present age = 7 × 4 = 28 years

Question 10.
The number of boys and girls in a class are in the ratio 7 : 5. The number of boys is 8 more than the number of girls. What is the total class strength ?
Solution:
Let the ratio be x.
The number of boys = 7x
The number of girls = 5x
According to the question
7x – 5x = 8
or, 2x = 8
∴ x = 4
Therefore number of boys = 7 × 4 = 28
The number of girls = 5 × 4 = 20
The total class strength = 28 + 20 = 48.

Question 11.
Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than Baichung’s. The sum of the ages of all the three is 135 years. What is the age of each one of them?
Solution:
Let Baichung’s age be x years.
Baichung’s Father age
= x + 29 years
Baichung’s Grand father age
= x + 29 + 26
= x + 55 years.
The sum of the ages of all the three is 135 years
∴ x + x + 29 + x + 55 = 135
or, 3x + 84 = 135
or, 3x = 135 – 84 = 51
x = \(\frac{51}{3}\) = 17
Baichung’s age = 17 years
Baichung’s father age
= 17 + 29 = 46 years
Baichung’s grandfather age
= 17 + 55 = 72 years

Question 12.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age ?
Solution:
Let Ravi’s present age be x years
15 years later Ravi’s age
= x + 15 years
According to the question
4x = x + 15
or, 4x – x =15
or, 3x = 15
∴ x = 5 years
Ravi’s present age = 5 years

Question 13.
A rational number is such that when you multiply it by \(\frac{5}{2}\) and add \(\frac{2}{3}\) to the product, you get \(\frac{-7}{12}\) number ?
Solution:
Let the number be x.
x is multiply by \(\frac{5}{2}\) = \(\frac{5x}{2}\) and \(\frac{2}{3}\)
∴ \(\frac{5x}{2}\) + \(\frac{2}{3}\) = \(\frac{7}{12}\)

Therefore, the rational number is \(\frac{-1}{30}\).

Question 14.
Lakshmi is a cashier in a bank. She has currency notes of denominations Rs. 100, Rs. 50 and Rs. 10, respectively. The ratio of the number of these notes is 2:3:5. The total cash with Lakshmi is Rs. 4,00,000. How many notes of each denomination does she have ?
Solution:
Let the ratio be x
Number of Rs. 100 notes
= 2x
Value = Rs. 100 × 2x
= Rs. 200x
Number of Rs. 50 notes
= 3x
Value = Rs. 100 × \(\frac{3x}{2}\)
= Rs. 150x
(∵ Rs.50 notes = 3x, Rs. 100 notes = \(\frac{3x}{2}\))
Number of Rs. 10 notes = 5x
Value = Rs 100 × \(\frac{5x}{10}\) = 50x
According to the question
200x + 150x + 50x = 4,00,000
or, 400x = 4,00,000
x = 1000
Number of Rs. 100 notes
= 2 × 1000 = 2000
Number of Rs. 50 notes
= 3 × 1000 = 3000
Number of Rs. 10 notes
= 5 × 1000 = 5000

Question 15.
I have a total of Rs. 300 in coins of denomination Re. 1, Rs. 2 and Rs. 5. The number of Rs. 2 coins is 3 times the number of Rs. 5 coins. The total number of coins is 160. How many coins of each denomination are with me ?
Solution:
The total number of coins = 160
Let the number of Re. 1 coins be x
Value = Rs. x
Number of Rs. 5 coins be y (let)
Value = Rs. 5y
Number of Rs. 2 coins
= 3y
Value = Rs. 6y
∴ x + y + 3y = 160
x + 5y + 6y = 300
or, x + 4y = 160 …(i)
and x + lly = 300 … (ii)
Subtract (i) from (ii)
we get 7y = 140
y = 20
From (i) x + 4 × 20 = 160
x + 80 = 160
x = 160 – 80 = 80
Number of Re. 1 coins = 80
Number of Rs. 5 coins = 20
Number of Rs. 2 coins
= 3 × 20 = 60

Question 16.
The organisers of an essay competition decide that a winner in the competition gets a prize of Rs. 100 and a participant who does not win gets a prize of Rs. 25. The total prize money distributed is Rs. 3,000. Find the number of winners, if the total number of participants is 63.
Solution:
The total number of participants is 63.
Let the number of winner be x.
Winners get Rs. 100 x
Number of participants who does not win = 63 – x
They get Rs. (63 – x) × 25
According to the question
100x + (63 – x) × 35
= 3000
or, 100x + 1575 – 25x = 3000
or, 75x + 1575 = 3000
or, 75x = 3000-1575
or, 75x = 1425
or, x = \(\frac{1425}{75}\) ∴ 19
∴ Number of winners = 19

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.1

Question 1.
Solve the following equations:
1. x – 2 = 7
2. y + 3 = 10
3. 6 = z + 2
4. \(\frac{3}{7}\) + x = \(\frac{17}{7}\)
5. 6x = 12
7. \(\frac{2x}{3}\) = 18
8. 1.6 = \(\frac{y}{1.5}\)
9. 7x – 9 = 16
10. 14y – 8 = 13
11. 17 + 6P = 9
12. \(\frac{x}{3}\) + 1 = \(\frac{7}{15}\)
Solution:
1. x – 2 = 7
or x – 2 + 2 = 7 + 2 (adding 2 both sides)
∴ x = 9

2. y + 3 = 10
y + 3 – 3 = 10 – 3 (subtract 3 from both sides)
∴ y = 7

3. 6 = x + 2
6 – 2 = z + 2 – 2 (subtract 2 from both sides)
4 = z
∴ z = 4

4. \(\frac{3}{7}\) + x = \(\frac{17}{7}\)
x = \(\frac{17}{7}\) – \(\frac{3}{7}\) = \(\frac{14}{7}\) = 2
∴ x = 2

5. 6x = 12
or \(\frac{6x}{6}\) = \(\frac{12}{6}\) (divide both side by 6)
∴ x = 2

6. \(\frac{t}{5}\) = 10
or \(\frac{t}{5}\) × 5 = 10 × 5 (multiply both sides by 5)
∴ t = 50

7. \(\frac{2x}{3}\) = 18
or 2x = 18 × 3
∴ x = \(\frac{18 \times 3}{2}\) = 9 × 3 = 27
∴ x = 27

8. 1.6 = \(\frac{y}{1.5}\)
or y = 1.6 × 1.5 = 2.40
∴ y = 2.4

9. 7x – 9 = 16
or 7x – 9 + 9 = 16 + 9 (adding 9 both sides)
or 7x = 25
∴ x = \(\frac{25}{7}\)

10. 14y – 8 = 13
14y – 8 + 8 = 13 + 8 (adding 8 both sides)
or 14y = 21
or y = \(\frac{21}{14}\) = \(\frac{3}{2}\)
∴ y = \(\frac{3}{2}\)

11. 17 + 6P = 9
17 + 6P – 17 = 9 – 17 (subtract -17 from both sides)
or 6P = -8
or P = \(\frac{-8}{6}\) = \(\frac{-4}{3}\)
∴ P = \(\frac{-4}{3}\)

12. \(\frac{x}{3}\) + 1 = \(\frac{7}{15}\)
or \(\frac{x}{3}\) + 1 – 1 = \(\frac{7}{15}\) – 1 (subtract 1 from both sides)
or \(\frac{x}{3}\) = \(\frac{7-15}{15}\)
or \(\frac{x}{3}\) = \(\frac{-8}{15}\)
∴ x = \(\frac{-8}{15}\) × 3 = \(\frac{-8}{5}\)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 1 Rational Numbers Exercise 1.2

Question 1.
Represent these numbers on the number line, (i) \(\frac{7}{4}\) (ii) \(\frac{-5}{6}\)
Solution:
(i) To represent \(\frac{7}{4}\), we make 7 marking of distance \(\frac{1}{4}\) each on the right of zero and starting from 0. The seventh marking is \(\frac{7}{4}\).

(ii) \(\frac{-5}{6}\)
To represent \(\frac{-5}{6}\), the number line may be divided into six equal parts. We make 6 marking of distance \(\frac{1}{6}\) each on the left of zero and starting from 0. The fifth marking is \(\frac{-5}{6}\).

Question 2.
Represent \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\) on the number line.
Solution:
To represent \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\). The number line may be divided into eleven equal parts. We make 11 marking of distance \(\frac{1}{11}\) each on the left of zero and starting from 0. The second fifth and ninth making are \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\)

Question 3.
Write five rational numbers which are smaller than 2.
Solution:
We can take 0, 2 because 0 is smaller than 2.
2 can be written as \(\frac{20}{10}\) and 0, as \(\frac{0}{10}\)
Thus we have \(\frac{19}{10}\), \(\frac{18}{12}\), \(\frac{17}{10}\), \(\frac{16}{10}\), \(\frac{15}{10}\) ……………. \(\frac{1}{10}\) between 2 and 0. You can take any five of these.

Question 4.
Find ten rational numbers between \(\frac{-2}{5}\) and \(\frac{1}{2}\).
Solution:

You can take any ten of these.

Question 5.
Find five rational numbers between:
(i) \(\frac{2}{3}\) and \(\frac{4}{5}\)
(ii) \(\frac{-3}{2}\) and \(\frac{5}{3}\)
(iii) \(\frac{1}{4}\) and \(\frac{1}{2}\)
Sol.

Second Method
We know, if a and b are two rational numbers, then
\(\frac{a+b}{2}\) is a rational number between a and b such that a < \(\frac{a+b}{2}\) < b.
Solution:
Find the mean of the given rational numbers

We now find another rational number between \(\frac{2}{3}\) and \(\frac{22}{30}\).
For this, we again find the mean of \(\frac{2}{3}\) and \(\frac{22}{30}\). That is

Question 6.
Write five rational numbers greater than -2.
Solution:
We can take -2,0 (0 is greater than -2).You can also take other number such that -2 < other number.
-2 = \(\frac{-20}{10}\)
0 = \(\frac{0}{10}\)
Thus we have \(\frac{-19}{10}\), \(\frac{-18}{10}\), \(\frac{-17}{10}\), \(\frac{-16}{10}\) …………………. \(\frac{0}{10}\)

Question 7.
Find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\).
Solution:

You can take any ten of these.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 1 Rational Numbers Exercise 1.1

Question 1.
Using appropriate properties find:
(i) \(\frac{2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
(ii) \(\frac{2}{5} \times\left(\frac{-3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)
Solution:
(i) \(\frac{2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)

2nd Method

3rd Method

(ii) 1st Method
\(\frac{2}{5} \times\left(\frac{-3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)

2nd Method

Question 2.
Write the additive inverse of each of the following:
(i) \(\frac{2}{8}\)
(ii) \(\frac{-5}{9}\)
(iii) \(\frac{-6}{5}\)
(iv) \(\frac{2}{-9}\)
(v) \(\frac{19}{-6}\)
Solution:
\(\frac{-2}{8}\) is the additive inverse of \(\frac{2}{8}\) because

\(\frac{-6}{5}\) is the additive inverse of \(\frac{6}{5}\) because

Question 3.
Verify that – (-x) = x for
(i) x = \(\frac{11}{15}\)
(ii) x = \(-\frac{13}{17}\)
Solution:
(i) We have, x = \(\frac{11}{15}\)
The additive inverse of

Question 4.
Find the multiplicative inverse of the following :
(i) -13
(ii) \(\frac{-13}{19}\)
(iii) \(\frac{1}{5}\)
(iv) \(\frac{-5}{8} \times \frac{-3}{7}\)
(v) -1 × \(\frac{-2}{5}\)
(vi) -1
Solution:
(i) Let the multiplicative inverse of -13 be x.
∴ -13 × x = 1

(v) Let the multiplicative inverse of -1 × \(\frac{-2}{5}\) be x.
∴ -1 × \(\frac{-2}{5}\) × x = 1
⇒ x = \(\frac{1 \times 5}{-1 \times(-2)}\) = \(\frac{5}{2}\) or \(\frac{-5}{-2}\)
(vi) The multiplicative inverse of -1 is -1 because -1 × (-1) = 1

Question 5.
Name the property under multiplication used in each of the following:
(i) \(\frac{-4}{5} \times 1=1 \times \frac{-4}{5}=-\frac{4}{5}\)
(ii) \(-\frac{13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}\)
(iii) \(\frac{-19}{29} \times \frac{29}{-19}\) = 1
Solution:
(i) 1 is the multiplicative identity. (ii) Commutativity, (iii) Multiplicative inverse.

Question 6.
Multiply \(\frac{6}{13}\) by the reciprocal of \(\frac{-7}{16}\).
Solution:
The reciprocal of \(\frac{-7}{16}\) is \(\frac{16}{-7}\)
The Product of \(\frac{6}{13}\) and \(\frac{16}{-7}\)
= \(\frac{6}{13}\) × \(\frac{16}{-7}\) = \(\frac{96}{-91}\)

Question 7.
Tell what property allows you to compute \(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right)\) as \(\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}\)
Solution:

We know for any three rational numbers a, b and c, a × (b × c) = (a × b) × c
The multiplication is associative for rational numbers.

Question 8.
Is \(\frac{8}{9}\) the multiplicative inverse of -1\(\frac{1}{8}\) ? Why or why not?
Solution:
No, the multiplicative inverse of \(\frac{8}{9}\) is \(\frac{9}{8}\) or 1\(\frac{1}{8}\).
Here, -1\(\frac{1}{8}\) is negative. Therefore, \(\frac{8}{9}\) is not multiplicative inverse of -1\(\frac{1}{8}\).

Question 9.
Is 0.3 the multiplicative inverse of 3\(\frac{1}{3}\) ? Why or why not?
Solution:
0.3 = \(\frac{3}{10}\)
Here, 0.3 × 3\(\frac{1}{3}\) = \(\frac{3}{10}\) × \(\frac{10}{3}\) = 1
We say that a rational number \(\frac{c}{d}\) is called the reciprocal or multiplicative inverse of another a rational number \(\frac{a}{b}\) if \(\frac{a}{b}\) × \(\frac{c}{d}\) = 1
∴ The result will be yes.

Question 10.
Write :
(i) The rational number that does not have a reciprocal.
Solution:
Zero has no reciprocal.

(ii) The rational numbers that are equal to their reciprocals.
Solution:
1 is equal to its reciprocal, because the reciprical of 1 is 1.
-1 is also equal to its reciprocal because the reciprocal of-1 is -1.
-1 × (-1) = 1

(iii) The Rational number that is equal to its negative.
Solution:
Its value negative.

Question 11.
Fill in the blanks :
(i) Zero has ……………. reciprocal.
(ii) The numbers …………….. and ……………. are their own reciprocals.
(iii) The reciprocal of -5 is …………
(iv) Reciprocal of \(\frac{1}{x}\), where x ≠ 0 is …………
(v) The product of two rational number is always a ……………..
(vi) The reciprocal of a positive rational number is ………………
Answer:
(i) no
(ii) 1.1
(iii) \(\frac{1}{-5}\)
(iv) x
(v) rational number
(vi) positive

Haryana State Board HBSE 8th Class Maths Solutions Chapter 1 Rational Numbers InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 1 Rational Numbers InText Questions

Try These (Textbook Page No. 4)

Question 1.
Fill in the blanks in the following table :
Answer:

Try These (Textbook Page No. 6)

Question 1.
Complete the following table :
Answer:

Try These (Textbook Page No. 9)

Question 1.
Complete the following table :
Answer:

Try These (Textbook Page No. 13)

Question 1.
Find using distributivity :
(i) \(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}\) + \(\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
(ii) \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}\) + \(\left\{\frac{9}{16} \times \frac{-3}{9}\right\}\)
Solution:

Try These (Textbook Page No. 17)

Question 1.
Write the rational number for each point labelled with a letter.
(i)
(ii)
Solution: