Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.5 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Exercise 2.5
Solve the following linear equations
Question 1.
\(\frac{x}{2}-\frac{1}{5}\) = \(\frac{x}{3}+\frac{1}{4}\)
Solution:
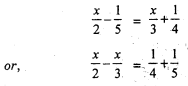

Question 2.
\(\frac{n}{2}\) – \(\frac{3n}{4}\) + \(\frac{5n}{6}\) = 21
Solution:

![]()
Question 3.
x + 7 – \(\frac{8x}{3}\) = \(\frac{17}{6}\) – \(\frac{5x}{2}\)
Solution:

Question 4.
\(\frac{x-5}{3}\) = \(\frac{x-3}{5}\)
Solution:
\(\frac{x-5}{3}\) = \(\frac{x-3}{5}\)
or, 5(x – 5) = 3 (x – 3)
or, 5x – 25 = 3x – 9
or, 5x – 3x = -9 + 25
or, 2x = 16
or, x = \(\frac{16}{2}\)
∴ x = 8
![]()
Question 5.
\(\frac{3t-2}{4}\) – \(\frac{2t-3}{3}\) = \(\frac{2}{3}\) – t
Solution:

or, 3 (13t – 18) = 24
or, 39t – 54 = 24
or, 39t = 24 + 54 = 78
or, 39t = 78
or, t = 2
Question 6.
m – \(\frac{m-1}{2}\) = 1 – \(\frac{m-2}{3}\)
Solution:
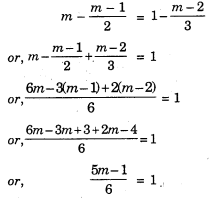
or, 5m – 1 = 6
or, 5m = 6 + 1
or, 5m = 7
∴ m = \(\frac{7}{5}\)
![]()
Simplify and solve the following linear equations:
Question 7.
3 (t – 3) = 5 (2t + 1)
Solution:
3 (t – 3) = 5 (2t + 1)
or, 3t – 9 = 10t + 5
or, 3t – 10t = 5 + 9
or, -7t = 14
or, t = \(-\frac{14}{7}\) =-2
t = -2
Question 8.
15(y – 4) – 2(y – 9) + 5(y + 6) = 0
Solution:
15(y – 4) – 2(y – 9) + 5(y + 6) = 0
or, 15y – 60 – 2y + 18 + 5y + 30 = 0
or, 20y – 2y – 60 + 48 = 0
or, 18y – 12 = 0
or, 18y = 12
or, y = \(\frac{12}{18}\) = \(\frac{2}{3}\)
∴ y = \(\frac{2}{3}\)
![]()
Question 9.
3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
Solution:
3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
or, 15z – 21 – 18z + 22 = 32z – 52 – 17
or, 15z – 18z – 32z = -52 – 17 + 21 – 22
or, 15z – 50z = 21 – 91
or, -35z = -70
or, 35z = 70
or, z = 2
∴ z = 2
Question 10.
0.25 (4f – 3) = 0.05 (10f – 9)
Solution:
0.25 (4f – 3) = 0.05 (10f – 9)
or, f – 0.75 = 0.5f – 0.45
or, f – 0.5f = -0.45 + 0.75
or, 0.5f = 0.3
f = \(\frac{0.3}{0.5}\) = \(\frac{3}{5}\) = 0.6
∴ f = 0.6