Haryana State Board HBSE 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.2 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 1 Rational Numbers Exercise 1.2
Question 1.
Represent these numbers on the number line, (i) \(\frac{7}{4}\) (ii) \(\frac{-5}{6}\)
Solution:
(i) To represent \(\frac{7}{4}\), we make 7 marking of distance \(\frac{1}{4}\) each on the right of zero and starting from 0. The seventh marking is \(\frac{7}{4}\).
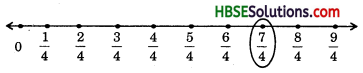
(ii) \(\frac{-5}{6}\)
To represent \(\frac{-5}{6}\), the number line may be divided into six equal parts. We make 6 marking of distance \(\frac{1}{6}\) each on the left of zero and starting from 0. The fifth marking is \(\frac{-5}{6}\).
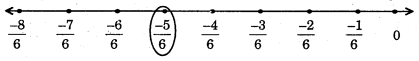
Question 2.
Represent \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\) on the number line.
Solution:
To represent \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\). The number line may be divided into eleven equal parts. We make 11 marking of distance \(\frac{1}{11}\) each on the left of zero and starting from 0. The second fifth and ninth making are \(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\)
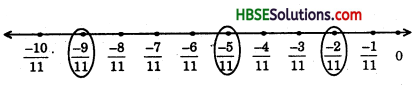
![]()
Question 3.
Write five rational numbers which are smaller than 2.
Solution:
We can take 0, 2 because 0 is smaller than 2.
2 can be written as \(\frac{20}{10}\) and 0, as \(\frac{0}{10}\)
Thus we have \(\frac{19}{10}\), \(\frac{18}{12}\), \(\frac{17}{10}\), \(\frac{16}{10}\), \(\frac{15}{10}\) ……………. \(\frac{1}{10}\) between 2 and 0. You can take any five of these.
Question 4.
Find ten rational numbers between \(\frac{-2}{5}\) and \(\frac{1}{2}\).
Solution:
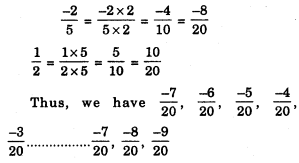
You can take any ten of these.
![]()
Question 5.
Find five rational numbers between:
(i) \(\frac{2}{3}\) and \(\frac{4}{5}\)
(ii) \(\frac{-3}{2}\) and \(\frac{5}{3}\)
(iii) \(\frac{1}{4}\) and \(\frac{1}{2}\)
Sol.

Second Method
We know, if a and b are two rational numbers, then
\(\frac{a+b}{2}\) is a rational number between a and b such that a < \(\frac{a+b}{2}\) < b.
Solution:
Find the mean of the given rational numbers
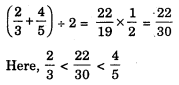
We now find another rational number between \(\frac{2}{3}\) and \(\frac{22}{30}\).
For this, we again find the mean of \(\frac{2}{3}\) and \(\frac{22}{30}\). That is

Question 6.
Write five rational numbers greater than -2.
Solution:
We can take -2,0 (0 is greater than -2).You can also take other number such that -2 < other number.
-2 = \(\frac{-20}{10}\)
0 = \(\frac{0}{10}\)
Thus we have \(\frac{-19}{10}\), \(\frac{-18}{10}\), \(\frac{-17}{10}\), \(\frac{-16}{10}\) …………………. \(\frac{0}{10}\)
![]()
Question 7.
Find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\).
Solution:

You can take any ten of these.