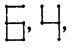Class 7

Haryana State Board HBSE 7th Class Maths Solutions Chapter 14 Symmetry Ex 14.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 14 Symmetry Exercise 14.2

Question 1.
Use tracing paper to decide which of the following figures have rotational symmetry :

Solution:
Fig. (a), (d), (e) and (f) have rotational symmetry.

Question 2.
Give the order of rotational symmetry for each figure :


Solution:

Haryana State Board HBSE 7th Class Maths Solutions Chapter 14 Symmetry Ex 14.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 14 Symmetry Exercise 14.1

Question 1.
Copy the figures with punched holes and find the axis of symmetry for the

Solution:

Ifone half a shape can be folded into other half, then the shape is said to have a line of symmetry or axis of symmetry, shapes which have one or two lines of symmetry are called symmetrical.
(a) Line of symmetry,
(b) Line of symmetry.
(c) Line of symmetry,
(d) Not symmetry.
(e) Line of symmetry.
(f) Not symmetry.
(g) Line of symmetry.
(h) Line of symmetry.
(i) Not symmetry.
(j) Line of symmetry.
(k) Line of symmetry.
(l) Not symmetry

Question 2.
Given the find the other hole line(s) of symmetry, find the other holes(s):

Solution:

Question 3.
In the following figures, the mirror line (i.ethe line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure.

Solution:

Question 4.
The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.

Identify multiple lines of symmetry, if any, in each of the following figures :


Solution:


i.e., Fig. (b), (d), (e), (g) and (h) are the multiple lines of symmetry.

Question 5.
Copy the figure given here. (Fig.)
Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that ? Will the figure be symmetric about both the diagonals ?
Solution:

Question 6.
Copy the diagram and complete each shape to be symmetric about the mirror line(s):

Solution:

Question 7.
State the number of lines of symmetry for the following figures :
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectangle
(f) A Rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle
Solution:
Shape :: No. of lines of Symmetry
(a) An equilateral triangle :: Three
(b) An isosceles triangle :: One
(c) A scalene triangle :: Nill
(d) A square :: Four
(e) A rectangle :: Two
(f) A Rhombus :: Two
(g) A parallelogram :: Nill
(h) A quadrilateral :: Nill
(i) A regular hexagon :: Six
(j) A circle :: Infinite

Question 8.
What letters of the English alphabet have reflectional symmetry i.e., symmetry related to mirror reflection) about, (a) a vertical mirror; (6) a horizontal mirror; (c) both horizontal and vertical mirrors.
Solution:
The English alphabets A to Z having
(a) Vertical lines of mirrors reflectional symmetry (like A) are
A, H, I, M, O, T. U, V, W, X, and Y.
(b) Horizontal lines of 1 mirrors reflectional symmetry (like B) are
B, C, D, E, H, I, K, O, and X.
(c) Both horizontal and
vertical lines of mirrors reflectional symmetry (like H) are H, 1,0 and X

Question 9.
Identify three examples of shapes with no line of symmetry.
Solution:

Question 10.
What other name can you give to the line of symmetry of
(a) an isosceles triangle ?
(b) a circle ?
Solution:
(a) an isosceles triangle : Right angled triangle.
(b) a circle : Semi-circle.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 13 Exponents and Powers InText Questions

Try These (Page 250)

Question 1.
Find five more such examples, where a number is expressed in exponential form. Also identify the base and the exponent in each case.
Solution:
(i) 64 = 4 × 4 × 4 = 4³
4³ = 4 is the base and 3 is exponent.

(ii) 1625 = 5 × 5 × 5 × 5 = 5⁴
5⁴ = 5 is the base and 4 is the exponent.

(iii) 64= 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
2⁶ = 2 is the base and 6 is the exponent.

(iv) 9 = 3 × 3 = 3²
3² = 3 is the base and 2 is the exponent.

(v) 343 = 7 × 7 × 7 = 7³
7³ = 7 is the base and 3 is exponent.

Try These (Page 251)

Question 1.
Express:
(i) 729 as a power of 3
(ii) 128 as a power of 2
(iii) 343 as a power of 7.
Solution:
(i) 729 = 3 × 3 × 3 × 3 × 3 × 3 = 3⁶,
So we can say that 729 = 3⁶.
(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2⁷
So we can say that 128 = 27.
(iii) 343 = 7 × 7 × 7 = 7³
So we can say that 343 = 7³.

Try These (Page 254)

Question 1.
Simplify and write in exponential form:
(i) 2⁵ × 2³
(ii) p³ × p²
(iii) 4³ × 4²
(iv) a³ × a² × a⁷
(v) 5³ × 5⁷x 5¹²
(vi) (-4)¹⁰⁰ × (-4)²⁰
Solution:
(i) 2⁵ × 2³ = (2 × 2 × 2 × 2 × 2) x (2 × 2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2^{5 + 3} = 2⁸.

(ii) p³ × p² = (p × p × p) × (p × p)
= p³⁺² = p⁵

(iii) 4³ × 4² = (4 × 4 × 4) × (4 × 4)
= 4^{3 + 2} = 4⁵

(iv) a³ × a² × a⁷ = a × a × a × a × a × a × a × a × a × a × a × a = a^{3 + 2 + 7} = a¹².

(v) 5³ × 5⁷x 5¹²
= 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5¹²
= 5^{3 + 7 + 12} = 5²²

(vi) (-4)¹⁰⁰ × (-4)²⁰
= 4¹⁰⁰ × (-4)²⁰ = 4¹²⁰.

Try These (Page 255)

Question 1.
Simplify and write in exponential: 11⁶ 4-11² = 11⁴.
(i) 2⁹ ÷ 2³
(ii) 10⁸ ÷ 10⁴
(iii) 9¹¹ ÷ 9⁷
(iv) 20¹⁵ ÷ 20¹³
(v) 7¹³ ÷ 7¹⁰
Solution:
(i) 29 ÷ 23 = 2^9-3 = 2⁶
(ii) 10⁸ ÷ 10⁴ = 10^8-4 = 10^8-4
(iii) 9¹¹ ÷ 9⁷ = 9^11-7 = 9⁴
(iv) 20¹⁵ ÷ 20¹³ = 20^15-13 = 20²
(v) 7¹³ ÷ 7¹⁰= 7^13-10 = 7³

Try These (Page 255)

Question 1.
Simplify and write the answer in exponential form :
(i) (6²)⁴
(ii) (2²)¹⁰⁰
(iii) (7⁵⁰)²
(iv) (5³)⁷
Solution:
(i) (6²)⁴ = 6^2×4 = 6⁸.
(ii) (2²)¹⁰⁰
= 2^{2 × 100} = 2²⁰⁰.
(iii) (7⁵⁰)² = 7 ^{50 × 2} = 7¹⁰⁰.
(iv) (5³)⁷ = 53^{3 × 7} = 5²¹.

Try These (Page 256)

Question 1.
Put into another form using a^m × b^m = (ab)^m
(i) 4³ × 2³
(ii) 2⁵ × b⁵
(iii) a² × t²
(iv) 5⁶ × (-2)⁶
(v) (- 2)⁴ × (- 3)⁴
Solution:
(i) 4³ × 2³ = (4 × 2)³ = 8³.
(ii) 2⁵ × b⁵ = (2 × b)⁵ = (2b)5.
(iii) a² × t² = (ax t)² = (at)².
(iv) 5⁶ × (-2)⁶ = [5 × (- 2)]⁶ = (- 10)⁶.
(v) (- 2)⁴ × (- 3)⁴= [(- 2) × (- 3)]⁴ = (6)⁴.

Try These (Page 257)

Question 1.
Put into another form using
a^m b^m = \(\left(\frac{a}{b}\right)^{m}\)
(i) 4⁵ ÷ 3⁵
(ii) 2⁵ ÷ b⁵
(iii) (-2)³ ÷ b⁵
(iv) p⁴ ÷ q⁴
(v) 5⁶ ÷ (-2)⁶
Solution:

Try These (Page 261)

Question 1.
Expand by expressing powers of 10 in the exponential form :
(i) 172
(ii) 5,643
(iii) 56,439
(iv) 176,428
Solution:
(i) 172 = 1 × 100 + 7 × 10 + 2
= 10² + 6 × 10¹ + 2 × 10⁰.

(ii) 5,643 = 5 × 1000 + 6 × 100 + 4 × 10 + 3
5 × 10³ + 6 × 10² + 4 × 10¹ + 3 × 10⁰.

(iii) 56, 439 = 5 × 10000 + 6 × 1000 + 4 × 100 + 3 × 10 + 9
= 5 × 10⁴ + 6 × 10³ + 4 × 10² + 3 × 10 + 9 × 10⁰

(iv) 176,428
= 1 × 100000 + 7 × 10000 + 6 × 1000 + 4 × 100 + 2 × 10 + 8
= 1 × 10⁶ + 7 × 10⁴ + 6 × 10³ + 4 × 10² + 2 × 10 + 8 × 10°.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers Ex 13.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 13 Exponents and Powers Exercise 13.1

Question 1.
Find the value of:
(i) 2⁶
(ii) 9³
(iii) 11²
(iv) 5⁴
Solution:
(i) 2⁸ = 2 × 2 × 2 × 2 × 2 × 2
= 64. Ans.
(ii) 9³ = 9 × 9 × 9 = 729. Ans.
(iii) 11² = 11 × 11 = 121. Ans.
(iv) 5⁴ = 5 × 5 × 5 × 5 = 625. Ans.

Question 2.
Express the following in
exponential from:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b x b × 6 × 6
(iv) 5 × 5 x 7 x 7 x 7
(v) 2 × 2 × a × a
(vi) axaxaxcxcxcxcxd
Solutoon:
(i) 6 × 6 × 6 × 6 = 6⁴
(ii) t × t = t²
(iii) b × b × b × b = 6⁴
(iv) 5 × 5 × 7 × 7 × 7= 5² × 7³
(v) 2 × 2 × a × a = 2² × a²
(vi)a xaxaxcxcxcxcxd
= a³ × c⁴ × d¹ .

Question 3.
Express each of the following numbers using exponential notation:
512 (ii) 343 (iii) 729 (iv) 3125
Solution:
(i) 512 = 8 × 8 × 8 = 8³ Ans.
(ii) 343 = 7 × 7 × 7 = 7³ Ans.
(iii) 729 = 9 × 9 x9 = 729. Ans.
(iv) 3125 = 5 × 5 × 5 × 5 × 5 = 5⁵ Ans.

Question 4.
Identify the greater number, whever possible, in each of the following ?
(i) 4³ or 3⁴
(ii) 5³ or 3⁵ (iii) 2¹⁰ or 8²
(iv) 100² or 2¹⁰⁰ (iv) 2¹⁰ or 10²
Sol.
(i) 4³ = 4 × 4 × 4 = 64 ,
3⁴= 3x3x3x3 = 81 34 > 43. Ans.

(ii) 5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
.•. 3⁵ > 5³. Ans.

(iii) 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 256
8² = 8 × 8 = 64
8² < 2⁸. Ans.

(iv) 100² or 2¹⁰⁰ i.e., 100²
= 100×100 = 10000
2¹⁰⁰ = 2 × 2 × 2 × 2 x 2 × 2
= 2¹⁰⁰
2¹⁰⁰ > 100². Ans.

(v) 2¹⁰ or 10² i.e.,2¹⁰
= 2 × 2 × ………………… x 2 = 2¹⁰
10² = 10 × 10 = 100
.-. 2¹⁰ > 10². Ans.

Question 5.
Express each of the following as product of powers of their prime factors :
(i) 648 (ii) 405 (Hi) 540 (iv) 3600
Sol.
(i) 648 = 2 × 324 = 2 × r. × 162
= 2 × 2 × 2 × 81
= 2 × 2 × 2 × 9 × 9
= 2 × 2 × 2 × 3 × 3 × 3 × 3
= 2³ × 3⁴. Ans.

405 = 3 × 135
= 3 × 3 × 45
= 3 × 3 × 3 × 3 × 15
= 3 × 3 × 3 × 3 × 5
= 3⁴ × 5¹. Ans.

540 = 2 × 270
= 2 × 2 × 135
= 2 x 2 x 3 x 45
= 2 x 2 x 3 x 3 x 15
= 2 × 2 × 3 × 3 × 3 x 5
= 2² × 3³ × 5¹. Ans.

3600 = 2 × 1800
= 2 × 2 × 900
= 2 × 2 × 2 × 450
= 2 × 2 × 2 × 2 × 225
= 2 × 2 × 2 × 2 × 3 × 75
= 2 × 2 × 2 × 2 × 3 × 3 × 25
= 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 2⁴ × 3² × 5⁴. Ans.

Question 6.
Simplify :
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 3² × 10⁴
Solution:
(i) 2 × 10³ = 2 × 10 × 10 × 10
= 2 × 1000 = 2000 Ans.
(ii) 7² × 2² = 7 × 7 × 2 × 2
= 49 × 4 = 196. Ans.

(iii) 2³ × 5 = 2 × 2 × 2 × 5
= 8 × 5 = 40. Ans.

(iv) 3 × 4⁴ = 3 × 4 × 4 × 4 × 4
= 768. Ans.

(v) 0 × 10² = 0 × 10 × 10 = 0. Ans.

(vi) 5² × 3³ = 5 × 5 × 3 × 3 × 3
= 25 × 27 = 675 Ans.

(vii) 2⁴ × 3² = 2 × 2 × 2 × 2 × 3 × 3
= 16 × 9 = 144. Ans.

(viii) 3² × 10⁴ = 3 × 3 × 10 × 10 × 10 × 10
= 9 × 10000 = 90000. Ans.

Question 7.
Simplify:
(i) (-4)³
(ii) (-3) × (-2)³
(iii) (- 3)² × (- 5)²
(iv) (- 2)³ × (- 10)⁴
Solution:
(i) (- 4)³ = – 4 × – 4 × – 4 = – 64. Ans.
(ii)(-3) x(-2)³ = – 3 × -2 × -2 × -2 = – 3 × – 8 = 24. Ans.
(iii) (- 3)² × (- 5)² = – 3 x – 3 x-5x – 5
= 9 × 25 = 225. Ans.
(iv) (- 2)³ × (- 10)⁴ = – 2 x – 2x – 2x – 10 × – 10 × – 10 × – 10
= -8 x 10000 = -80000 Ans.

Question 8.
Compare the following numbers:
(i) 2.7 ’ × 1012; 1.5 x10s
(ii) 4 x : 10u; 3 × 1017.
Sol. (i) 27
2.7 × 10¹² = \(\frac{27}{10}\) × 10 × 10¹¹
= 27 × 10¹¹
= 3 × 3 × 3 × 10¹¹
= 3³ × 10¹¹
1.5 × 10⁸ = \(\frac{15}{10}\) × 10 × 10⁷
= 15 × 10⁷
= 3 × 5 × 10⁷
3³ × 10¹¹ > 3 × 5 × 10⁷
or 2.7 × 10¹² > 1.5 × 10⁸

(ii) 4 x 10¹⁴; 3 × 10¹⁷
4 × 10¹⁴ = 4 × 10¹⁴
and 3 × 10¹⁷ = 3 × 10¹⁷
3 × 10¹⁷ > 4 × 10¹⁴. Ans.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers Ex 13.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 13 Exponents and Powers Exercise 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² x 3⁴ x 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ x a²
(iv) 7^x x 7²
(v) (5²)³ ÷ 5³
(vi) 2⁵ x 5⁵
(vii) a⁴ x b⁴
(viii) (3⁴)³
(ix) (2⁵⁰ ÷ 2¹⁵) x 2³
(x) 8^t ÷ 8²
Solution:
(i) 3² x 3⁴ x 3⁸ = 3^{2 + 4 + 8} = 3¹⁴
(ii) 6¹⁵ 6¹⁰ = \(\frac{6^{15}}{6^{10}}\) = 6^{15 – 10} = 6⁵
(iii) a³ x a² = a³⁺² = a⁵
(iv) 7^x x 7² = 7^x+2
(v) (5²)³ ÷ 5³ = \(\frac{5^{6}}{5^{3}}\) = 5^6-3 = 5³.
(vi) 2⁵ x 5⁶ = (2 x 5)⁵ = 10⁵.
(vii) a⁴ x b⁴ = (ab)⁴.
(viii) (3⁴)³ = 3^{4 x 3} = 3¹².

(ix) (2²⁰ ÷ 2¹⁵) x 2³ = \(\frac{2^{20}}{2^{15}}\) x 2³
=2^20-15 x 2³
= 2⁵ x 2³ = 2⁵⁺³ = 2⁸.

(x) 8^t ÷ 8² = \(\frac{8^{t}}{8^{2}}\) = 8^t-2.

Question 2.
Simplify and express each of the following in exponential form :

Solution:


(vi) 2° + 3° + 4° = 2°(1 + 2°) + 3° .
(vii) 2° x 3° x 4° = (2 x 3 x 4)° = (24)°.
(viii) (3° + 2°) x 5° = (1 + 1) x 1
= 2 x 1 = 2¹.

(xii) (2³ x 2)² = 2^{3 x 2} x 2²
= 2⁶ x 2² = 2⁶⁺² = 2⁸

Question 3.
Say true or false and justify your answer:
(i) 10 x 10¹¹ = 100¹¹
(ii) 2³ x 5²
(iii) 2³ x 3² = 6⁵
(iv) 3⁰ = (1000)⁰
Solution:
10 x 10¹¹ = 100¹¹
= 10^{1 + 11} = 10¹²
= (10²)¹¹ = 10²²
L.H.S ≠ R.H.S
10 x 10¹¹ = 100¹¹ is false.

(ii) 2³ > 5²
L.H.S. 2³ = 8
R.H.S. 5² = 25
∴ 5² > 2³
2³ > 5² is false.

(iii) 2³ x 3² = 65
L.H.S. 2³ x 3²
R.H.S.
6⁵ = (2 x 3)⁵ = 2⁵ x 3⁵
∴ L.H.S. ≠ R.H.S.
∴ 2³ x 3² = 6⁵ is false.

(iv) 3⁰ = (1000)⁰
L.H.S.
3⁰
R.H.S.
1000⁰ = (10³)⁰
∴ L.H.S. ≠ R.H.S.
∴ 3⁰ = (1000)⁰ is false.

Question 4.
Express each of the following as a product of prime factor only in exponential form:
(i) 108 x 192
(ii) 270
(iii) 729 x 64
(iv) 768
Solution:
(i) 108 x 192
= 2 x 2 x 3 x 3 x 3 x 2 x 2 x 2 x 2 x 2 x 2 x 3
= 2⁸ x 3⁴.

(ii) 270
= 2 x 5 x 3 x 3 x 3
= 2 x 5 x 3³.

(iii) 729 x 64
= 3 x 3 x 3 x 3 x 3 x 3 x 2 x 2 x 2 x 2 x 2 x 2
= 3⁶ x 2⁶ = (3 x 2)⁶.

Question 5.
Simplify :
(i) \(\frac{\left(2^{5}\right)^{2} \times 7^{3}}{8^{3} \times 7}\)
(ii) \(\frac{25 \times 5^{2} \times t^{8}}{10^{3} \times t^{4}}\)
(iii) \(\frac{3^{5} \times 10^{5} \times 25}{5^{7} \times 6^{5}}\)
Solution:

Haryana State Board HBSE 7th Class Maths Solutions Chapter 13 Exponents and Powers Ex 13.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 13 Exponents and Powers Exercise 13.3

Question 1.
Write the following number in the expanded forms:
279404, 3006194, 2806196, 120719, 20068.
Solution:
279404
= 2 x 100000 + 7 x 10000 + 9 x 1000 + 4 x 100 + 0 x 10 + 4
= 2 x 10⁵ + 7 x 10⁴ + 9 x 10³ + 4 x 10² + 0 x 10¹ + 4 x 10⁰

3006194
= 3 x 1000000 + 0 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 4
= 3 x 10⁶ + 0 x 10⁵ + 0 x 10⁴ + 6 x 10³ + 1 x 10² + 9 x 10¹ + 4 x 10⁰

2806196
= 2 x 1000000 + 8 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 6
= 2 x 10⁶ + 8 x 10⁵ + 0 x 10⁴ + 6 x 10³ + 1 x 10²
+ 9 x 10¹ + 6 x 10⁰.

120719 = 1 x 100000 + 2 x 10000 + 0 x 1000 + 7 x 100 + 1 x 10 + 9.
= 1 x 10⁵ + 2 x 10⁴ + 0 x 10³ + 1 x 10²
+ 1 x 10¹+ 9 x 10⁰

20068
= 2 x 10000 + 0 x 1000 + 0 x 100 + 6 x 10 + 8.
= 2 x 10⁴ + 0 x 10³ + 0 x 10² + 6 x 10¹ + 8 x 10⁰.

Question 2.
Find the number from each of the following expanded forms:
(i) 8 x 10⁴ + 6 x 10³ + 0 x 10² + 4 x 10¹ + 5 x 10⁰
(ii) 4 x 10⁵ + 5 x 10³ + 3 x 10²+ 2 x 10⁰
(iii) 3 x 10⁴+ 7 x 10² + 5 x 10⁰
(iv) 9 x 10⁵ + 2 x 10² + 3 x 10¹.
Solution:
(i) 8 x 10⁴ + 6 x 10³ + 0 x 10² + 4 x 10¹ + 5 x 10⁰
= 8×10000 + 6×1000 + 0x100 + 4×10 + 5×1
= 80000 + 6000 + 0 + 40 + 5
= 86045.

(ii) 4 x 10⁵ + 5 x 10³ + 3 x 10²+ 2 x 10⁰
= 4 x 100000 + 5 x 1000 + 3 x 100 + 2 x 1
= 405302

(iii) 3 x 10⁴+ 7 x 10² + 5 x 10⁰
= 3 x 10000 + 7 x 100 + 5 x 1
= 30000 + 700 + 5 = 30705

(iv) 9 x 10⁵ + 2 x 10² + 3 x 10¹.
= 9 x 100000 + 2 x 100 + 3 x 1
= 900000 + 200 + 3 = 900203.

Question 3.
Express the following number in standard form :
(i) 50,000,000
(ii) 70,00,000
(iii) 3,186,500,000
(iv) 390878
(v) 39087.8
(vi) 3908.78
Solution:
(i) 50,000,000 = 5.0 x 10000000
= 5.0 x 10⁷.
(ii) 70,00,000 = 7.0 x 1000000
= 7.0 x 10⁶
(iii) 3,186,500,000
= 3.1865 x 1000000000
= 3.1865 x 10⁹.
(iv) 390878 = 3.90878 x 100000
= 3.90878 x 10⁵.
(v) 39087.8 = 3.90878 x 10000
= 3.90878 x 10⁴.
(vi) 3908.78 = 3.90878 x 1000
= 3.90878 x 10³.

Question 4.
Express the number appearing in the following statements in standard form.
(a) The mean distance between Earth and Moon is 384,000,000.
(b) The speed of light in vaccum is 300.000. 000 m/s.
(c) Diameter of the Earth is 12756000 m.
(d) Diameter of the sun is 1,400,000,000 m.
(e) In a galaxy there are on an average 100.000. 000.000 stars.
(f) The universe is estimated to be as out 12.000. 000.000years old.
(g) The distance of the sun from the centre of the Milky way Galaxy ios estimated to be 3,00,000,000,000,000,000,000 m.
(h) 60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8gm.
(i) The earth has 1,353,000,000 cubic km of sea water.
(j) The population of India was about 1,027,000, 000 in March, 2001.
Solution:
(a) 3,84,000,000 = 3.84 x 100000000 = 3.84 x 10⁸ m.
(b) 300,000,000 m/s
= 3.0 x 100000000 = 3.0 x 10⁸ m/s.
(c) 12756000 m
= 1.2756 x 10000000 = 1.2756 x 10⁷ m.
(d) 1,400,000,000 m
= 1.4 x 1000000000 = 1.4 x 10⁹ m.

(e) 1,00,000,000,000 stars
= 1.0 x 100000000000 = 1.0 x 10¹¹ stars.
(f) 12,000,000,000 years old
= 2.0 x 1000000000 = 12.0 x 10⁹ year old.
(g) 300,000,000,000,000,000,000 m.
= 3.0 x 100000000000000000000 m.
= 3.0 x 10²⁰ m.
(h) 60,230,000,000,000,000,000,000 molecules of water in 1.8 gm.
= 6.023 x 10000000000000000000000
= 6.023 x 10²² molecules of water in 1.8 gm.
(i) 1,353,000,000 cubic km.
= 1.353 x 1000000000
= 1.353 x 10⁹ cubic km.
(j) 1,027,000,000 population of India in March in 2001.
= 1.027 x 1000000000 = 1.027 x 10⁹ population of India in March 2001.

Haryana State Board HBSE 6th Class Sanskrit Solutions Ruchira Chapter 4 विद्यालयः Textbook Exercise Questions and Answers.

Haryana Board 6th Class Sanskrit Solutions रुचिरा Chapter 4 विद्यालयः

अभ्यासः

प्रश्न 1.
उच्चारणं कुरुत
अहम्, आवाम्, वयम्, माम्, आवाम्, अस्मान्, मम्, आवयोः, अस्माकम्, त्वम्, युवाम्, यूयम्, त्वाम् युवाम्, युष्मान्, तव, युवयोः, युष्माकम्।।
उत्तरम्:
छात्र स्वयं प्रयास करें।

प्रश्न 2.
निर्देशानुसारं परिवर्तनं कुरुतयथा-
अहं पठामि। (बहुवचने) – वयं पठामः।
(क) अहं नृत्यामि। – (बहुवचने) – ……………….
(ख) त्वं पठसि। – (बहुवचने) – ………………….
(ग) युवां क्रीडथः। – (एकवचने) – …………………
(घ) आवां गच्छावः। – (बहुवचने) – ………………
(ङ) अस्माकं पुस्तकानि। – (एकवचने) – …………….
(च) तव गृहम्। – (द्विवचने) – ………………..
उत्तरम्:
(क) वयं नृत्यामः
(ख) यूयं पठथ
(ग) त्वं क्रीडसि
(घ) वयं गच्छामः
(ङ) मम पुसतकम्
(च) युवयोः गृहे

प्रश्न 3.
कोष्ठकात् उचितं शब्दं चित्वा रिक्तस्थानानि पूरयत-
(क) ……………………………. पठामि। (वयम्/अहम्) |
(ख) …………………………. गच्छथः। (युवाम्/यूयम्)
(ग) एतत् ……………………………. पुस्तकम्। (माम/मम)
(घ) ………………… क्रीडनकानि। (युष्मान्/युष्माकम्)
(ट) ………………………. छात्रे स्वः। (वयम/आवाम)
(च) एषा ………………… लेखनी। (तव/त्वाम) |
उत्तरम्:
(क) अहम्
(ख) युवाम्
(ग) मम
(घ) युष्माकम्
(ङ) आवाम
(च) तव

प्रश्न 4.
क्रियापदैः वाक्यानि पूरयत
पठसि, धावामः, गच्छावः, क्रीडथः, लिखामि, पश्यथ
यथा- अहं पठामि।
उत्तरम्:
(क) त्वं
(ख) आवां
(ग) यूयं
(घ) अहं
(ङ) युवां
(च) वयं
उत्तरम्:
(क) पठसि
(ख) गच्छावः
(ग) पश्चथ
(घ) लिखामि
(ङ) क्रीडथः
(च) धावामः

प्रश्न 5.
उचितपदैः वाक्यनिर्माणं कुरुत-
मम, तव, आवयोः, युवयोः, अस्माकम्, युष्माकम्

यथा- एषा मम पुस्तिका।
(क) एतत् …………………………… गृहम्।
(ख) ………………….. मैत्री दृढा।
(ग) एषः ………………………….. विद्यालयः।
(घ) एषा ……………………… अध्यापिका।
(ङ) भारतम् ………………………. देशः।
(च) एतानि ………………………. पुस्तकानि।
उत्तरम् :
(क) तव
(ख) आवयोः
(ग) मम
(घ) युवयोः
(ङ) अस्माकम्
(च) युष्माकम्।

प्रश्न 6.
एकवचनपदस्य बहुवचनपदं, बहुवचनपदस्य एकवचनपदं च लिखत-
यथा- एषः – एते
(क) सः – ……………..
(ख) ताः – ……………..
(ग) एताः – ……………..
(घ) त्वम् – ……………..
(ङ) अस्माकम् – ……………..
(च) तव – ……………..
(छ) एतानि – ……………..
उत्तरम्:
(क) ते
(ख) सा
(ग) एषा
(घ) यूयम्
(ङ) मम
(च) युष्माकम्
(छ) एतत्।

प्रश्न 7.
(क) वार्तालापे रिक्तस्थानानि पूरयत
यथा- प्रियंवदा – शकुन्तले! त्वं किं करोषि?
शकुन्तला – प्रियंवदे! ………… नृत्यामि, ………….. किं करोषि?
प्रियंवदा – शकुन्तले! …………. गायामि। किं …………. न गायसि?
शकुन्तला – प्रियंवदे! ………….. न गायामि। …………… तु नृत्यामि।
प्रियंवदा – शकुन्तले! किं …………….. माता नृत्यति।
शकुन्तला – आम्, …………. माता अपि नृत्यति।
प्रियंवदा – साधु, …………. चलावः।
उत्तरम् :
अहं, त्वं, अहं, त्वं, अहं, अहं, तव, मम, आवाम्।

(ख) उपयुक्तेन अर्थेन सह योजयत-
शब्दः – अर्थ
सा – तुम दोनों का
तानि – तुम सब
अस्माकम् – मेरा
यूयम् – वह (स्त्रीलिङ्ग)
आवाम् – तुम्हारा
मम – वे (नपुंसकलिङ्ग)
युवयोः – हम दोनों
तव – हमारा
उत्तरम्:
सा – वह (स्त्रीलिङ्ग)
तानि – वे नपुंसकलिङ्ग
अस्माकम् – हमारा
यूयम् – तुम सब
आषाम् – हम दोनों
मम – मेरा
युवयो: – तुम दोनों का
तव – तुम्हारा।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 Algebraic Expressions InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 Algebraic Expressions InText Questions

Try These (Page 230)

Question 1.
Describe how the following expression are obtained:
7xy + 5, x²y, 4x² – 5x
Solution:
(i) 7xy + 5, we first obtain xy, multiply it by 7 to get Ixy and add 5 to Ixy to get the expression.
(ii) x²y, we first obtain x² and multiply it by y.
(iii) 4x² – 5x, we first obtain x² and multiply it by 4 to get 4x². From 4x², we subtract 5x to finally arrive at 4x² – 5x.

Try These (Page 231)

Question 1.
What are the terms in the following expressions ? Show how the terms are formed. Draw a tree diagram for each expression:
8y + 3x², 7mn – 4, 2x²y.
Solution:
8y + 3x² : The above expression 8y + 3x² consists two terms 8y and 3x². The terms 8y is product of 8 and y. And the term 3x² is product of 3, x and x.

7mn – 4: The above expression 7mn – 4 consist two terms 7mn and -4. The term 7mn is product of 7, m and n and the term – 4 has only one factor, that is – 4.

2x2y: The above expression consist only one term 2x2y. The product of the term 2x2y is 2,x, 2 andy or2 xxx 2 xy.

Try These (Page 231)

Question 1.
Identify the co-efficients of the following expressions:
4x – 3y, a + b + 5, 2y + 5, 2xy.
Solution:

Try These (Page 233)

Question 1.
Group the like terms together from the following:
12x 12, – 25x, -25, -25y, 1,x, 12y, y.
Solution:
12x, – 25x, x are like terms.
– 25y, 12y, y are like terms.

Try These (Page 233)

Question 1.
Classify the following expressions as a monomial, a binomial or a trinomial: a, a + b, ab + a + b, ab + a + b – 5, xy + 5, 5x² – x + 2,4pq -3q + 5p, 7,4m -7n + 10, 4mn + 7.
Solution:
a is a monomial.
a + b is a binomial.
ab + a + b is a trinomial.
ab + a + b – 5 is not a trinomial, because it contains 4 terms.
So it is polynomial.
xy + 5 is a binomial.
5x² – x + 2 is trinomial.
4pq -3q + 5p is trinomial.
7 is monomial.
4m -7n + 10 is trinomial.
4mn + 7 is binomial.

Try These (Page 236)

Question 1.
Sarita’s father’s age is 5 years more than 3 times Sarita’s age. What is her father’s age ?
Solution:
Since, Sarita’s father’s age is 5 years (y) more than 3 times Sarita’s age.
Therefore, her father’s age = (3y + 5) years.

Question 2.
The length of a rectangular hall is 4 metres less than 3 times the breadth of the hall. What is the length, if the breadth is b metres ?
Solution:
Let the breadth of the hall be b metres. Since, its length is 4 metres less than 3 times the breadth of the hall.
∴ Length of the hall = (3b – 4) metres.

Try These (Page 238)

Question 1.
Add and subtract:
(i) m – n, m + n
(ii) mn + 5 – 2, mn + 3.
Solution:
(i) Adding (m – n) and (m + n) we have m -n + m + n = m + m = 2m
∴ The sum = 2m
Subtract: m – n – (m + n)
= m – n – m – n
= -n-n
= -2n
∴ The difference is -2n.

(ii) Adding mn + 5 – 2 and mn + 3, we have (mn + 5 – 2) + mn + 3
= mn + 5 – 2 + mn + 3
= (mn + mn) + (5 – 2 + 3)
= 2 mn + 6
∴ The sun = 2mn + 6.
Subtract : (mn + 3) from (mn + 5-2), we have
(mn + 5 – 2) – (mn + 3)
= mn + 5 – 2 – mn – 3
= 0 + 3 – 3 = 0
∴ The difference is 0.

Try These (Page 245)

Question 1.
Make similar pattern with basic figures as shown:

(The number of segments required to make the figure is given to the right. Also, the expression for the number of segments required to make n shapes is also given).
Solution:

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 Algebraic Expressions Ex 12.4 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 Algebraic Expressions Exercise 12.4

Question 1.
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic calculators.


If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to from 5, 10, 100 digits of the kind

Solution:
(a) If n = 4
∴ 5n + 1 = 5 × 4 + 1 = 20 + 1 = 21

If n = 5
∴ 5n + 1 = 5 × 5 + 1 = 25 + 1 = 26

If n = 10
∴ 5n + 1 = 5 × 10 + 1 = 50 + 1 = 51

If n = 100
∴ 5n + 1 = 5 × 100 + 1 = 500 + 1 = 501

(b) n = 4
3n + 1 = 3 × 4 + 1 = 12 + 1 = 13

If n = 5,
3n + 1 = 3 × 5 + 1 = 15 + 1 = 16

If n = 10
3n + 1 = 3 × 10 + 1 = 30 + 1 = 31

If n = 100
3n + 1 = 3 × 100 + 1 = 300 + 1 = 301

(c) If n = 4
5n+ 2 = 5 × 4 + 2 = 20 + 2 = 22

If n = 5
5n + 2= 5 × 5 + 2 = 25 + 2 = 27

If n = 10
5n + 2 = 5 × 10 + 2 =50+ 2 = 52

If n = 100
5n + 2 = 5 × 100 + 2 =500 + 2 = 502

Question 2.
Use the given algebraic expression to complete the table of number patterns (sequences):

Solution:
(1) If n = 100
2n – 1 = 2 × 100 – 1 = 200 – 1 = 199

(2) If n = 5
3n + 2 = 3 × 5 + 2 = 15 + 2 = 17

If n = 10
3n + 2 = 3 × 10 + 2 = 30 + 2 = 32

If n = 100
3n + 2 = 3 × 100 + 2 = 300 + 2 = 302

(3) If n = 5
4n + 1 = 4 × 5 + 1 = 20 + 1 = 21

If n = 10
4n + 1 = 4 × 10 + 1 = 40 + 1 = 41

If n = 100
4n + 1 = 4 × 100 + 1 = 400 + 1 = 401

(4) If n = 5, 7n + 20 = 7 × 5 + 20
= 35 + 20 = 55

If n = 10, 7n + 20 = 7 × 10 + 20
= 70 + 20 = 90

If n = 100, 7n + 20 = 7 × 100 + 20
= 700 + 20 = 720

(5) If n = 5, n² + 1 = 5 × 5 + 1
= 25 + 1 = 26

If n = 10, + n² = 10 × 10 + 1
= 100 + 1 = 101

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 Algebraic Expressions Ex 12.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 Algebraic Expressions Exercise 12.3

Question 1.
If m = 2, find the value of:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) \(\frac{5 m}{2}\) – 4
Solution:
(i) m – 2 – 2 – 2 = 0
(ii) 3m – 5 = 3(2) – 5 = 6 – 5 = 1
(iii) 9 – 5 m = 9 – 5(2) = 9 – 10 = – 1.
(iv) 3m² – 2m – 7
= 3(2)² – 2(2) – 7
= 3 × 4 – 4 – 7
= 12 – 4 – 7 = 8 – 7 = 1
(v) \(\frac{5 m}{2}\) – 4 = \(\frac{5 \times 2}{2}\) – 4
= \(\frac{10}{2}\) – 4 = 5 – 4 = 1

Question 2.
If P = – 2, find the value of;
(i) 4p + 7
(ii) – 3p² + 4p + 7
(iii) – 2p² – 3p² + 4p + 7, when p = – 2.
Solution:
(i) 4p + 7 = 4(- 2) + 7 = – 8 + 7
= -1

(ii) – 3(-p)² + 4(-p) + 7
= – 3(- 2)² + 4(- 2) + 7
= – 3 × 4 + 4 × -2 + 7
= – 12 – 8 + 7
= – 13.

(iii)- 2p² – 3p² + 4p + 7
= -2(-2)² – 3(- 2)² + 4 × (- 2) + 7
= -2 × 4 – 3 × 4 + 4 × – 2 + 7
= -8 – 12 – 8 + 7
= -21.

Question 3.
Find the value of the following expressions, when x = – 1.
(i) 2x- 7
(ii) -x + 2
(iii) x² + 2x + 1
(iv) 2x² – x – 2.
Solution:
(i) 2x – 7 = 2(-1) – 7 = -2 – 7
= -9

(ii) -x + 2 = – (-1) + 2
= 1 + 2 = 3

(iii) x² + 2x + 1
= (- 1)² + 2(- 1) + 1
= 1 – 2 + 1 = 0.

(iv) 2x² – x – 2 = 2(- 1)² – (- 1) – 2
= 2 × 1 + 1 – 2
= 2 + 1 – 2
= 3 – 2 = 1.

Question 4.
If a = 2, b = – 2, find the value of:
(i) a² + b²
(ii) a² + ab + b²
(iii) a² – b2².
Solution:
(i) a² + b² = (2)² + (- 2)²
= 4 + 4
= 8

(ii) a² + ab + b² = (2)² + 2 x -2 + (-2)²
= 4 – 4 + 4
= 8 – 4 = 4.

(iii) a² – b² = (2)² – (- 2)²
= 4 – 4
= 0.

Question 5.
When a = 0, b = -1, find the value of the given expressions:
(i) 2a+2b
(ii) 2a² + b² + 1
(Hi) 2a²b + 2ab² + ab
(iv) a² + ab + 2.
Solution:
(i) 2a + 2b = 2 × 0 + 2(- 1)
= 0 + (- 2) = – 2

(ii) 2a² + b² + 1 = 2(0)² + (- 1)² + 1
= 2 × 0 + 1 + 1
= 1 + 1 = 2.

(iii) 2a²b + 2ab² + ab
= 2(0)² (- 1) + 2 × 0(- 1)² + 0 × – 1
= 2 × 0 × (-1) + 2 × 0 × 1 + 0
= 0 + 0 + 0 = 0

(iv) a² + ab + 2
a = 0
b = -1
= (0)² + (0) (- 1) + 2
= 0 + 0 + 2 = 2.

Question 6.
Simplify the expressions and find the value of x is 2.
(i) x + 7 + 4(x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x-2)
(iv) 4(2x – 1) + 3x + 11
Solution:
(i) x + 7 + 4(x – 5)
= x + 7 + 4x – 20
= 2 + 7 + 4 × 2 – 20
= 9 + 8 – 20
= 17 – 20 = – 3.

(ii) 3(x + 2) + 5x – 7
= 3x + 6 + 5x – 7
= 3 × 2 + 6 + 5 × 2 – 7
= 6 + 6 + 10 – 7
= 12 + 10 – 7
= 22 – 7 = 15.

(iii) 6x + 5(x – 2) = 6x + 5x – 10
= 6 × 2 + 5 × 2 – 10
= 12 + 10 – 10
= 22 – 10 = 12.

(iv) 4(2x – 1) + 3x + 11
= 8x – 4 + 3x + 11
= 8 x 2 – 4 + 3 x 2 + 11
= 16 – 4 + 6 + 11
= 12 + 6 + 11
= 18 + 11
= 29.

Question 7.
Simplify these expressions and find their yalue of x = 3, a = – 1, b = – 2,
(i) 3x – 5 -x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a.
Solution:
(i)3x – 5 – x + 9
= 3 × 3 – 5 – 3 + 9
= 9 – 5 – 3 + 9
= 4 – 3 + 9
= 1 + 9 = 10.

(ii) 2 – 8x + 4x + 4
= 2 – 8 × 3 + 4 × 3 + 4
= 2 – 24 + 12 + 4
= 18 – 24 = – 6.

(iii) 3a + 5 – 8a + 1
= 3(- 1) + 5 – 8(- 1) + 1
= -3 + 5 + 8 + 1
= 2 + 8 + 1 = 11.

(iv) 10 – 3b – 4 – 5b
= 10 – 3(-2) – 4 – 5(-2)
= 10 + 6 – 4 + 10
= 16 – 4 + 10 = 12 + 10
= 22.

(v) 2a -26-4-5 + a
= 2(-1) – 2(-2) – 4 – 5 + (-1)
= -2 + 4 – 4 – 5 – 1
= 2 – 9 – 1
= 2 – 10 = -8.

Question 8.
(a) If z = 10, find the value of z³ – 3(z -10).
(6) If p = -10 find the value of p² – 2p – 100.
Solution:
(a) z³ – 3(z -10)
= (10)³ – 3(10-10)
= 1000 – 3 x 0
= 1000 – 0 = 1000

(b) p² – 2p – 100 = (- 10)² – 2 x (- 10) – 100
= 100 + 20 – 100
= 120 – 100 = 20.

Question 9.
What should be the value of a if the value of 2x² + x – a equals to 5, when x = 0 ?
Solution:
2x² + x – a = 5
2(0)² + 0 – a = 5
or 2 x 0 + 0 – a = 5
or -a = 5 or a = -5

Question 10.
Simplify the expression and find its value when a = 5 and b = – 3, 2(a² + ab) + 3 – ab.
Solution:
2(a² + ab) + 3 – ab
= 2a² + 2ab + 3 – ab
= 2a² + ab + 3
= 2 × (5)² + (5) × (-3) + 3
= 2 × 25 + (- 15) + 3
= 50 – 15 + 3
= 53 – 15 = 38.