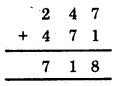
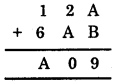
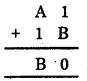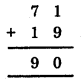HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers Ex 16.2
Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers Ex 16.2 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 16 Playing with Numbers Exercise 16.2
Question 1.
If 21y5 is a multiple of 9, where y is: a digit, what is the value of y ?
Solution:
Since 21y5 is a multiple of 9.
i.e. 21y5 is divisible by 9.
Therefore, 2 + 1 + y + 5 = (8 + y) must be a multiple of 9. i.e. (8 + y) should be divisible by 9.
This is possible when 8 + y = 9 or 18
⇒ 8 + y = 9 or 8 + y = 18
y = 1 or y = 10
But, since x is a digit, therefore y = 10 is not possible.
Thus y = 1.
Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z ?
You will find that there are two answers for the last problem. Why is this so ?
Solution:
Since 31z5 is divisible by 9.
∴ 3 + 1 + z + 5 = a multiples of 9.
9 + z = 9, 18 or 27
⇒ 9 + z = 9 9 + z = 18
⇒ z = 0 z = 9
9 + z = 27
z = 21
which is not a one digit number.
∴ The values of z are (0 or 9).
There are two values of z as the sum of digits is a multiple of 9. So, it may be 9, 18, 27 … any one of them.
![]()
Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x ?
[Hint: Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers : 0, 3, 6, 9, 12, 15, 18, … . But since a: is a digit, it can only be that 6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.]
Solution:
We have 24x is a multiple of 3.
∴ 2 + 4 + x = 6 + x
is a multiple of 3.
∴ 6 + x = 0, 3, 6, 9, 12, 15, …
But, x is a digit.
∴ It can only be that
6 + x = 6 or 9, 12 or 15
∴ x = 0, 3, 6 or 9.
Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z ?
Solution:
Since 31z5 is a multiple of 3.
∴ The sum of the digits (3 + 1 + z + 5) is a multiple of 3.
So, 9 + z is one of these numbers :
0, 3, 6, 9, 12, …
9 + z = 9 ⇒ z = 1
[Values less than 9 gives negative result]
9 + z = 12 ⇒ z = 3
9 + 2= 15 ⇒ z = 6
9 + z = 18 ⇒ z = 9
9 + z = 21 ⇒ z = 12
which is not a one digit number.
∴ The values of z are 1, 3, 6 or 9.
HBSE 8th Class Maths Solutions Chapter 16 Playing with Numbers Ex 16.2 Read More »