Haryana State Board HBSE 8th Class Maths Solutions Chapter 14 Factorization Ex 14.3 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 14 Factorization Exercise 14.3
Question 1.
Carry out the following-divisions :
(i) 28x4 ÷ 56x
(ii) -36y3 ÷ 9y2
(iii) 66pq2r3 ÷ 11qr2
(iv) 34x3y3z2 ÷ 51xy2z3
(v) 12a8b8 ÷ (-6a6b4)
Solution:

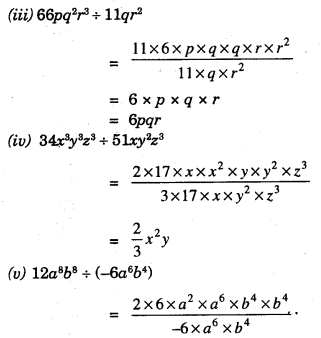
Question 2.
Divide the given polynomial by the given monomial.
(i) (5x2 – 6x) ÷ 3x
(ii) (3y8 – 4y6 + 5y4), y4
(iii) 8 (x4y2z2 + x2y3z2 + x2y2z2)
(iv) 9x2y2(3z – 24) ÷ 27xy(z – 8)
(v) 96abc(3a – 12) (5b – 30) ÷ 144 (a – 4) (b – 6)
Solution:

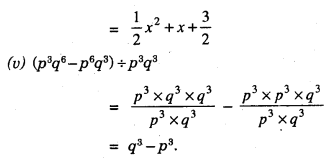
![]()
Question 3.
Work out the following divisions :
(i) (10x – 25) ÷ 5
(ii) (10x – 25) ÷ (2x – 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7)
(iv) 9x2y2(3z – 24) ÷ 27xy (z – 8)
(v) 96abc (3a -12) (5b – 30) ÷ 144 (a – 4) (b – 6)
Solution:

Question 4.
Divide as directed :
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
(ii) 26xy (x + 5) (y – 4) ÷ 13x (y – 4)
(iii) 52pqr (p + q) (q + r) (q + p) ÷ 104pq (q + r) (r + p)
(iv) 20 (y + 4) (y2 + 5y + 3) ÷ 5(y + 4)
(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
Solution:
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
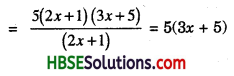
(ii) 26xy (x + 5) (y – 4) ÷ 13x (y – 4)
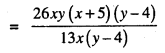
(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104pq (q + r) (r + p)
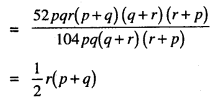
= 4(y2 + 5y + 3)
(iv) 20 (y + 4) (y2 + 5y + 3) ÷ 5 (y + 4)
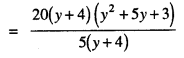
(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
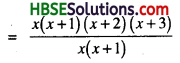
= (x + 2) (x + 3)
![]()
Question 5.
Factorise the expression and divide them as directed :
(i) (y2 + 7y + 10) ÷ (y + 5)
(ii) (m2 – 14m – 32) ÷ (m + 2)
(iii) (5p2 – 25p + 20) ÷ (p – 1)
(iv) 4yz (z2 + 6z – 16) ÷ 2y (z + 8)
(v) 5pq(p2 – q2) ÷ 2p(p + q)
(vi) 12xy(9x2 – 16y2) ÷ 4xy(3x + 4y)
(vii) 39y3(50y2 – 98) ÷ 26y2(5y + 7)
Solution:
(i) (y2 + 7y + 10) , (y + 5)
y2 + 7x + 10 = y2 + 5 + 2 + 10
= (y + 5) + 2(y + 5)
= (y + 5) (y + 2)
(ii) (m2 – 14m – 32) ÷ (m + 2)
m2 – 14m – 32 = m2 – 16m + 2m – 32
= m (m – 16) + 2 (m – 16)
= (m – 16) (m + 2)
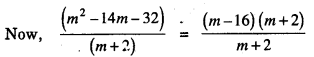
(iii) (5p2 – 25p + 20) ÷ (p – 1)
5p2 – 25p + 20 = 5p2 – 20p – 5p + 20
= 5p (p – 4) – 5(p – 4)
= (p – 4) (5p – 5)
= (p – 4) × 5(p – 1)
= 5 (p – 4) (p – 1)
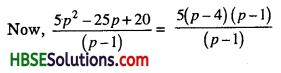
= 5 (p – 4)
(iv) 4yz(z2 + 6z – 16) ÷ 2y (z + 8)
z2 + 6z – 16 = z2 + 8z – 2z – 16
= z(z + 8) – 2 (2 + 8)
= (z + 8) (z – 2)
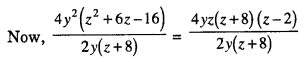
= 2z(z – 2)
(v) 5pq(p2 – q2) ÷ 2p(p + q)
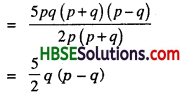
(vi) 12xy (9x2 – 16y2) + 4xy (3x + 4y)
9x2 – 16y2 = (3x)2 – (4y)2
= (3x + 4y) (3x – 4y)
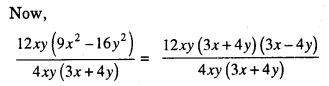
= 3(3x – 4y)
(vii) 39y3(50y2 – 98) + 26y2(5y + 7)
50y2 – 98 = 2(25y2 – 49)
= 2(5y)2 – (7)2]
= 2(5y + 7) (5y – 7)
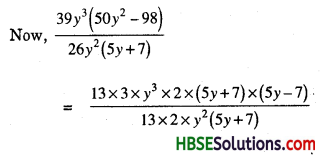
= 3y(5y – 7)