HBSE 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 Perimeter and Area  Exercise 11.2

Question 1.
Find the area of each of the following parallelograms :

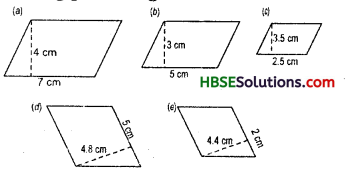
Solution:
(a) Length of base (6) = 7 cm
height (h) = 4 cm
∴ Area of the parallelogram
=6 x A = (7 x 4) cm² = 28 cm².

(b) The length of base = 5 cm height (h) = 3 cm
∴ Area of the parallelogram
= b x h = (5 x 3) cm² = 15 cm².

(c) The length of base = 2.5 cm
height (h) = 3.5 cm
∴ Area of the parallelogram
=b x h = (2.5 x 3.5) cm² = 8.75 cm².

(d) The length of base (6) = 5 cm
height (h) = 4.8 cm
∴ Area of the parallelogram
=b x h = (5 x 4.8) cm² = 24.0 cm².

(e) The length of base (b) = 2 cm
height (h) = 4.4 cm
∴ Area of the parallelogram
=b x h = (2 x 4.4) cm² = 24.0 cm².

Question 2.
Find the area of each of the following triangles:

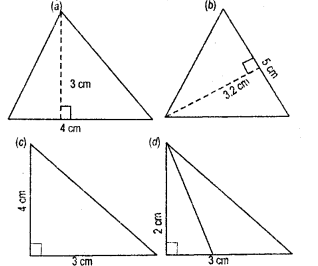
Solution:
(a) The length of base (b) = 4 cm
height (h) = 3
∴ Area of triangle = \(\frac{1}{2}\) x b x h = \(\frac{1}{2}\) x 3 x 4 = \(\frac{12}{2}\) = 6 cm².

(b) base (b) = 4 cm
height (h) = 3
∴ Area of triangle = \(\frac{1}{2}\) x b x h = \(\frac{1}{2}\) x 3 x 4 = \(\frac{16}{2}\) = 8 cm².

(c) base (b) = 3 cm
height (h) = 4
∴ Area of triangle = \(\frac{1}{2}\) x b x h = \(\frac{1}{2}\) x 3 x 4 = \(\frac{12}{2}\) = 6 cm².

(d) base (b) = 3 cm
height (h) = 2
∴ Area of triangle = \(\frac{1}{2}\) x b x h = \(\frac{1}{2}\) x 3 x 2 = \(\frac{6}{2}\) = 3 cm².

Question 3.
Find the missing values :

Base	Height	Area of the parallelogram
(a) 20 cm (b) …………. (c) …………. (d) 15.6cm	…………. 15 cm 8.4 cm ………….	246 cm2 154.5 cm2 48.72 cm2 16.38 cm2

Solution:
(a) Base = 20 cm,
Area of the parallellogram = 246 cm²
Height = \(\frac{\text { Area }}{\text { Base }}=\frac{246}{20}\) cm
= 12.3 cm
∴ The missing value (height) = 12.3 cm²

(b) Height = 15 cm,
∴ Area of the parallelogram = 154.5 cm²
Area of the parallelogram = b x h
⇒ 154.5 = b x 15
⇒ b = \(\frac{154.5}{15}\) = 10.3 cm
∴ The missing value (base)
= 10.3 cm

(c) Height = 8.4 cm,
Area of the parallelogram
= 48.72 cm²
Let the base of the parallelogram = b cm
∴ b x h = 48.72
⇒ b x 8.4 = 48.72
b = \(\frac{48.72}{8.4}\) = 5.8 cm
Thus, the missing value (base) = 5.8 cm

(d) Base (6) = 15.6 cm,
Area of the parallellogram
= 16.38 cm²
Let the height be = h cm
b x h = 16.38 cm²
⇒ 15.6 x h = 16.38 cm²
⇒ h = \(\frac{16.38 \mathrm{~cm}^{2}}{15.6 \mathrm{~cm}}\) = 1.05 cm.
Thus the missing value (height) = 1.05 cm

Question 4.
Find the missing value.

Base	Height	Area of the triangle
(a)    15 cm (b) …………. (b)   22 cm	…………. 31.4 mm ………….	87 cm2 1256 mm2 170.5 cm2

(i) Here,
Base(b) = 15 cm
Area of Triangle = 87cm²
Let Height = h
∴ Area of Triangle = \(\frac{1}{2}\) x b x h
⇒ 87 = \(\frac{1}{2}\) x 15 x h
⇒ 87 x 2 = 15h
⇒ \(\frac{87 \times 2}{15}\) = h
⇒ h = \(\frac{174}{15}\)
= 11.6 cm.
The missing value (height) = 11.6 cm

(ii) Here,
Height (h) = 31.4 mm
Area of Triangle = 1256 mm²
Let, Base = b mm
∴ \(\frac{1}{2}\) x b x h = 1256
⇒ \(\frac{1}{2}\) x 6 x 31.4 = 1256
⇒ b = \(\frac{2 \times 1256}{31.4}\)
∴ b = 80 mm
The missing value Base (b)
= 80 mm.

(iii) Here,
Base (b) = 22 cm
Area of Triangle = 170.5 cm2
Let, Height = h cm
∴ \(\frac{1}{2}\) x b x h = 170.5 cm²
⇒ \(\frac{1}{2}\) x 22 x h = 170.5 cm²
⇒ h = \(\frac{2 \times 170.5}{22}\) cm²
= 15.5 cm.

Question 5.
PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:

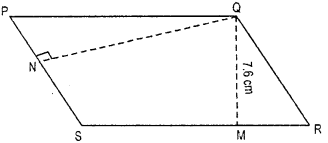
(a) the area of the parallelogram PQRS.
(b) QN, if PS = 8 cm.
Solution:
(a) QM (height) = 7.6 cm
SR (base) = 12 cm
∴ Area of parallelogram PQRS
= b x h = (12 x 7.6) cm² = 91.2 cm².

(b) QN (height) = ?
PS (base) = 8 cm.
and area of parallelogram PQRS = 91.2 cm²
∴ Area of parallelogram PQRS = base x height
91.2 cm² = 8 cm x h
or h = \(\frac{91.2 \mathrm{~cm}^{2}}{8 \mathrm{~cm}}\)
(QN)height = 11.4 cm.

Question 6.
DL and BM are the heights on sides AB & AD respectively of parallelogram ABCD. If the area of parallelogram is 1470
cm² and AB = 35 cm and AD = 49 cm. Find the length of BM and DL.

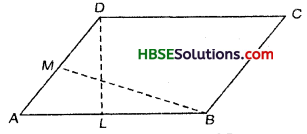
Solution:
In parallelogram ABCD,
AB (base) = 35 cm
∴ Area of parallelogram = 1470 cm²
DL (height) = ?
Area of parallelogram = b x h
h = \(\frac{1470}{35}\)
or, height (DL) = 42 cm
And AD(base) = 49 cm
BM (height) = ?
Area of parallelogram = 1470 cm²
∴ Area of parallelogram = b x h
1470 = 49 x h
or, h = \(\frac{1470}{49}\)
or, height (BM) = 30 cm.

Question 7.
ΔABC is right angle at A. AD is per-pendicular BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm. Find the area of AABC. Also find the length of AD.

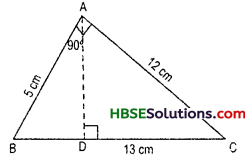
Solution:
In a right angled AABC,
base = 12 cm,
height = 5 cm
∴ Area of a right angled triangle = \(\frac{1}{2}\) x b x h
= \(\frac{1}{2}\) x 12 x 5
= 30 cm².
If base = 13 cm,
height (AD) = ?
Area = \(\frac{1}{2}\) xb x h = \(\frac{1}{2}\) x 13 x AD
or 30 cm² = \(\frac{13 \mathrm{AD}}{2}\)
or 13 AD = 30 x 2 = 60 cm²
∴ AD = \(\frac{60 \mathrm{~cm}^{2}}{13 \mathrm{~cm}}\) = 4.62cm
And, Second method : From Hero’s formula,

Question 8.
AABC is isosceles with AB = AC =
7,5 cm, and BC = 9 cm.
The height AD from A to BC is 6 cm. Find the area of ∆ABC. What will be the height from C to AB 8 i.e., CE.

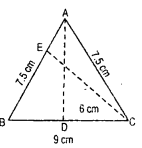
Solution:
In a ∆ABC, base = 9 cm
height = 6 cm
∴ Area of AABC = \(\frac{1}{2}\) x b x h
= \(\frac{1}{2}\) x 9 x 6 = 27 cm².
Now, In a ∆ABC, if base = 7.5 cm and
height = ?
∴ Area of a ABC = \(\frac{1}{2}\) x base x height
27cm² = \(\frac{1}{2}\) x 7.5 cm CE
or 7.5 cm x CE = 27 cm² x 2
or CE = \(\frac{54 \mathrm{~cm}^{2}}{7.5 \mathrm{~cm}}\)
∴ height, CE = 7.2