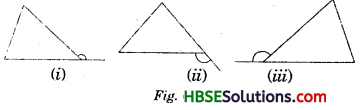Class 7

Haryana State Board HBSE 7th Class Maths Solutions Chapter 8 Comparing Quantities Ex 8.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 8 Comparing Quantities Exercise 8.3

Question 1.
Tell what is the profit or loss in the following transction. Also find profit % or loss % in each case.
(a) Gardening shears bought for Rs. 250 and sold for Rs. 325.
(b) A fridge bought for Rs. 12,000 arid sold at Rs. 13,500.
(c) A cupboard bought for Rs. 2500 and sold at Rs. 3000.
(d) A skirt bought for Rs. 250 and sold at Rs. 150.
Solution:
(a) C.P. = Rs. 250
S.P. = Rs. 325
Profit or gain = S.P. – C.P.
= 325 – 250 = Rs. 75
Gain % = \(\frac{\text { Gain }}{\text { C.P. }}\) x 100
= \(\frac{75}{250}\) x 100
∴ gain % = 30%
C.P. = Rs. 12,000,
S.P. = Rs. 13,500
Profit = 13,500-12,000
= Rs. 1,500
Profit % = \(\frac{1500}{12000}\) x 100 = 12\(\frac{1}{2}\)%

(c) C.P. = Rs. 2500 S.P. = Rs. 3000
Profit = 3000 – 2500 = Rs. 500
Profit % = \(\frac{500}{2500}\) x 100 = 20%

(d) C.P. = Rs. 250 S.P. = Rs. 150
Loss = C.P. – S.P.
= 250 – 150 = Rs. 100
Loss % = \(\frac{\text { Loss }}{\text { C.P. }}\) x 100
= \(\frac{100}{250}\) x 100 = 40%

Question 2.
Convert each part of the ratio to percentage:
(a) 3:1
(b) 2:3:5
(c) 1:4
(d) 1:2:5
Solution:
(a) Total part of Ratio = 3 + 1 = 4
= \(\frac{3}{4}=\frac{3}{4}\) x 100% = 75%
= \(\frac{1}{4}=\frac{1}{4}\) x 100% = 25%

(b) Total part of Ratio = 2 + 3 + 5 = 10

(c) Total part of Ratio =1 + 4 = 5

(d) Total part of ratio = l + 2 + 5 = 8

Question 3.
The population of a city decreased from 25000 to 24500. Find the percent decrease.
Solution:
Percent decrease

∴ Percent decrease = 2%.

Question 4.
Arun bought a car for Rs. 3,50,000. The next year, the price went upto Rs. 3,70,000. What was the percent increase ?
Solution:
Percent increase

Question 5.
I buy a T.V. for Rs. 10,000 and sell it at a profit of 20%. What do I get for it ?
Solution:
C.P. = Rs. 10,000, S.P. = ?
Profit = 20%

∴ S.P. = Rs. 12000
Profit = S.P. – C.P.
= 12000 -10000
∴ Profit = Rs. 2000

Question 6.
Juhi sells a washing machine for Rs. 13,500. She loses 20% in the bargain. What was the price at which she bought it ? Solution:
S.P. = Rs. 13,500, loss = 20%,
C.P. = ?

or 8 C.P. = 13500 x 10
∴ C.P = \(\frac{135000}{8}\) = Rs. 16875.

Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find percent of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick ?
Solution:
(i) Calcium : Carbon : Oxygen
= 10:3 : 12
Total part of Ratio = 10 + 3 + 12 = 25
Percent of calcium in chalk = \(\frac{10}{25}\) x 100% = 40%
Percent of carbon in chalk = \(\frac{3}{25}\) x 100% = 12%
Percent of oxygen in chalk = \(\frac{12}{25}\) x 100% = 48%

(ii) Let total weight of carbon = x
According to question, 12% of x = 3 gm
or, \(\frac{12}{100}\) x x = 3
x = \(\frac{3 x 100}{100}\) = 25
Hence total weight of carbon = 25 gm.

Question 8.
Amina buys a book for Rs. 275 and sells it at a loss of 15%. IIow much does she sell it for ?
Solution:
C.P. = Rs. 275, S.P. = ?
Loss = 15%
S.P = \(\left(\frac{100-\operatorname{Loss} \%}{100}\right)\) x 275 = Rs. 233.75

Question 9.
Find the amount to be paid at end of 3 years in each case :
(a) Principal = Rs. 1200 at 12% p.a.
(b) Principal = Rs. 7500 at 5%p.a.
Solution:
(a) S.I = \(\frac{\mathrm{PRT}}{100}\)
= \(\frac{1200 \times 12 \times 3}{100}\) = Rs. 432
A = P + I = 1200 + 432
= Rs. 1632

(b) S.I. = \(\frac{7500 \times 5 \times 3}{100}\) = Rs. 1125
A = P + I = 7500 + 1125
= Rs. 8625.

Question 10.
What is the rate of interest which gives an interest of Rs. 280 on a sum of Rs. 56000 for 2 years ?
Solution:
P =Rs. 56000,
S.I. = Rs. 280, T = 2 years,
R =?

.’. Rate of interest = 0.25%.

Question 11.
If Meena gives an interest of Rs. 45 for the one year at 9% rate p.a. What is sum she has borrowed ?
Solution:
S.I. = Rs. 45, R = 9%,
T = 1 year, P = ?
P = \(\frac{\text { S.I. } \times 100}{R \times T}=\frac{45 \times 100}{9 \times 1}\)
.’. Sum = Rs. 500.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 7 Congruence of Triangles Ex 7.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 7 Congruence of Triangles Exercise 7.2

Question 1.
Which congruence criterion do you use in the following ?
(a) Given:AC = DF
AB = DF
BC = EF
∴ ΔABC ≅ ΔDEF

(b) Given : ZX = RP
RQ = ZY

(c) Given:

(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
∴ ΔABE ≅ ΔCDB

Solution:
(a) In ΔABC and ΔDEF, we have
AC = DF (given)
AB = DE (given)
BC = EF (given)
Hence, ΔABC ≅ ΔDEF (By SSS congruence Criterion)

(b) In ΔPQR and ΔXYZ, we have
ZX = RP (given)
RQ = ZY (given)
∠PQR = ∠XYZ (given)
But included angle
∠PQR ≠ ∠XZY
So, SAS congrunce rule cannot be applied and we cannot conclude that the ΔPQR and ΔXYZ are cogruent.

(c) In ΔLMN and ΔGFH, we have
∠MLN = ∠FGH (given)
∠NML = ∠GFH (given) Included side between ∠MLN, ∠NML and ∠FGH, ∠GFH are
ML = GF
Hence ΔLMN ≅ ΔGFH (By ASA congruence Criterion)
(d) In ΔABE and ΔCDB, we have
EB = DB (given)
AE = BC (given)
∠A = ∠C = 90° (given)
i.e. ∠A =∠C = 90°
Side AE = SideBC hypotenuse EB = hypotenuse DB
Hence, ΔABE ≅ ΔCDB (By RHS Congruence Criterion)

Question 2.
You want to show that ΔART ≅ ΔPEN
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(b) If it is given that m∠T = m∠N and you are to use SAS criterion, you need to have

(i) R T =
and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have (i) ? (ii) ?
Solution:
(a) In ΔART and ΔPEN, we have
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
Hence, ΔART ≅ ΔPEN (By SSS congruence rule)

(b) In ΔART and ΔPEN, we have
∠T = ∠N
(i) RT = EN
(ii) AT = PN i.e., PN = AT
Hence, ΔART ≅ ΔPEN (By SAS Congruence Criterion)

(c) In ΔART and ΔPEN, we have
AT = PN
(i) ∠RAT = ∠EPN ⇒ A ⇔  P
(u) ∠RTA = ∠ENP ⇒ T ⇔ T
Hence, ΔART ≅ ΔEPN (By ASA Congruence Criterion)

Question 3.
You have to show that ΔAMP ≅ ΔAMQ. In the following proof, supply the missing reasons.

Solution:
In ΔAMP Δ AMQ
1. PM = QM ⇒ 1. PM = QM (one side of a right-angled triangle are respectively equal to the one side of another)
2. m∠PMA = m∠QMA ⇒ 2. ∠M = ∠M = 90°
3. AM = AM ⇒ 3. AM = AM = Common
4. ΔAMP ≅ ΔAMQ ⇒ 4. ΔAMP ≅  ΔAMQ (By SAS congruence rule)

Question 4.
In ΔABC, ∠A = 30° , ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠P = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified ? Why of why not ?
Solution:
In ΔABC and PQR, we have
∠A = ∠P = 30° (given)
∠B = ∠Q = 40° (given)
∠C = ∠R = 110° (given)

Using Angle sum property of triangle
∠A + ∠B + ∠C = 30° + 40° + 110°
= 180°
∠P+ ∠Q + ∠R = 30° + 40° + 110°
= 180°
If AB = PQ, BC = QR and AC = PR,
Hence ΔABC ≅ ΔPQR
(By AAA congruence criterion)

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write. ΔRAT s ?

Solution:
In ΔRAT and ΔWON, we have
RA = WO (given)
AT = ON (given)
included ∠RAT = included ∠WON
Hence ΔRAT ≅ ΔWON
(By SAS congruence rule)
or, In ΔRAT and ΔWON, we have
∠R = ∠W
∠A = ∠O
∠T = ∠N and if RT = WN
Hence ΔRAT ≅ ΔWON (By AAA congruence rule)

Question 6.
Complete the congruence statement:

Solution:
In ΔTBC
BA is the bisector of base TC
Hence, ∠BAC = ∠BAT = 90°
and AC = AT
Now, In ΔBCA and ΔBTA, we have
∠BAC = ∠BAT =90° (given)
and hypotenuse BC = hypotenuse BT (given)
and Side AC = side AT (given)
BA = BA = Common
Hence, ΔBCA ≅ ΔBTA
(By RHS congruence rule)
or, ΔBCA ≅ ΔBTA
(By SSS congruence rule)
and ; In ΔQRS and QPT, we have
QR = TP (given)
SR = QR (given)
SQ = QT (given)
∠R = ∠P (given)
∠RQS = ∠QTP
and included side QR = TP (given)
Hence, ΔQRS ≅ ΔQPT
(By SSS congruence rule)
and, ΔQRS ≅ ΔQTP
(By ASA congruence rule)

Question 7.
In a squared sheet, draw two triangles of equal areas such that:

(i) the triangles are congru¬ent.
(ii) the triangles are not con¬gruent.
What can you say answer their perimeters
Solution:
(i) In ΔABD and ΔCBD,
AD = BC = 4 cm (given)
AB = CD = 4 cm (given)
∠A = ∠C = 90° (given)
Hence, ΔABD ≅ ΔCBD (By SAS congruence rule)

(ii) In squared sheet, we have two triangles and two triangles are congrunet.
Hence, two triangles perimeters are equal.

Question 8.
If ΔABC and ΔPQR are to be congruent name one additional pair of corresponding parts. What criterion did you see ?

Solution:
Since ΔABC ≅ ΔPQR
Hence, ∠ABC = ∠RQP = 90°
Hypotenuse AC = Hypotenuse PR
Side AB = Side PQ
So, ΔABC ≅ ΔPQR
(By RHS congruence criterion)
or ∠B = ∠Q = 90
∠C = ∠R
Included side BC = included side QR
Hence ΔABC ≅ ΔPQR
(By ASA congruence criterion)

Question 9.
Explain, why ΔABC ΔFED

Solution:
∵ ∠B = ∠E (each 90°)
∠A = ∠F (given)
∠C = ∠D
(third angles are equal) Also BC = ED (given)
Two angles (∠B and ∠C) and included side BC of ΔABC are respectively equal to two angles (∠E and ∠D) and the included side ED of ΔDEF.
∴ ΔABC ≅ ΔFED.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 7 Congruence of Triangles Ex 7.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 7 Congruence of Triangles Exercise 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if
(b) Among two congruent angles one has a measure 70°; the measure of the other angle is .
(c) When we write ∠A ≅ ∠B we actually mean
Solution:
(a) their length are same.
(b) 70° (c) ∠A ≅ ∠B.

Question 2.
Give any two real-life examples for congruent shapes.
Solution:
(i) Ears
(ii) Eyes

Question 3.
If ∠ABC = ∠FED under the correspondence ABC ⇔ FED, write all the corresponding congruent parts of the triangles.

Solution:
If ΔABC ≅ ΔFED
then AB = FE
BC = ED
AC = FD
and ∠A = ∠F,
∠B =∠E and ∠C = ∠D.

Question 4.
If ΔDEF ≅ ΔBCA, write the part (s) of ABCA that correspond to
(i) ∠E
(ii) \(\overline{E F}\)
(iii) ∠F
(iv) \(\overline{D F}\)

(i) ∠E ⇔ ∠F
(ii) \(\overline{E F}\) ⇔ \(\overline{C A}\)
(iii) ∠F ⇔∠A
(iv) \(\overline{D F}\) ⇔ \(\overline{B A}\)

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties InText Questions

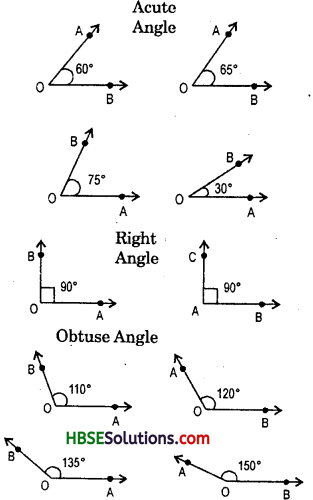
Try These (Page No. 113-114):

Question 1.
Write the six elements (i.e. the 3 sides and the 3 angles) of AABC.
Solution:
Six elements of ΔABC are : ∠A, ∠B, ∠C, \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\) and \(\overline{\mathrm{CA}}\).

Question 2.
Write the :
(i) Side opposite to
the vertex Q of B ΔPQR.
(ii) Angle opposite to the side LM of ΔLMN
(iii) Vertex oppostie to the side RT of ΔRST.
Solution:
A triangle is simple closed curve mode of three line segments. It has three vertices, three sides and three angles.

(i) Side opposite to the vertex Q of ΔPQR is PR.

(ii) Angle opposite to side LM of ΔLMN is ∠LMN

(iii) Vertex opposite to the side RT of ΔRST is S.

Question 3.
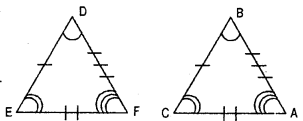
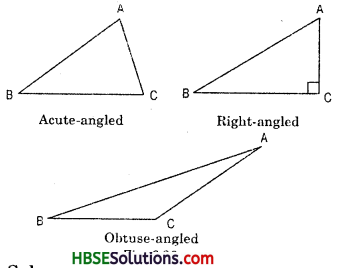
Look at the Fig. and classify each of the triangles according to its (a) Sides (b) Angles


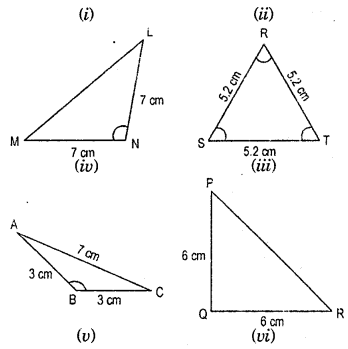
Solution:
(a) Sides : We may classify the triangles according to their sides as follows:
I. A triangle having no two sides equal is called a scalene triangle.
II. A triangle having two sides equal is called an isosceles triangle.
III. A triangle having all sides equal is called an equilateral triangle.
Hence, (ii) ΔPQR is scalene triangle.
(i) ΔABC, (iii) ΔLMN, (v) ΔABC and
(vi) ΔPQR are isosceles triangle, and;
(iv) ARST is equilateral triangle.

(b) Angles : According to angles :
I. A triangle, all of whose angles are acute, is called an acute angle triangle.
II. A triangle, one of whose angles is right angle, is called right angle triangle.
III. A triangle one of whose angles is obtuse, is called an obtuse angle triangle.
Hence, (i) ΔABC, (iv) ΔRST are acute angle triangle.
(ii) ΔPQR, (vi) ΔPQR arc right angle triangle.
(iii) ΔLMN, (v) ΔABC are obtuse angle triangle.

Think, Discuss & Write (Page No. 114):

Question 1.
How many medians can a triangle have? .
Solution:
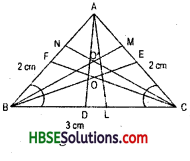
The line segment, joining the mid point to its opposite vertex are called a median of the triangle. In a triangle has three vertex. Hence in a triangle has three median. (Fig. 6.19)

Question 2.
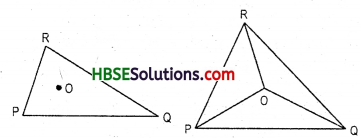
Does a median lie wholly in the interior of the triangle ? (If you think that this is not true, draw a figure to show such a case).
Solution:
In a triangle ABC three median AL, BM, CN meet the point O. Hence a median lie wholly in the interior of the triangle.

Think, Discuss & Write (Page No. 115):

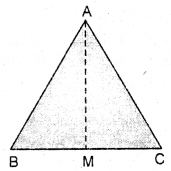
Question 1.
How many altitudes can a triangle have ?
Solution:
An altitude has one end point at a vertex of the triangle and the other on the line containing the opposite side. In a triangle has three vertex. So it has three altitude.
e.g. AD, BE, CF are altitude of triangle.

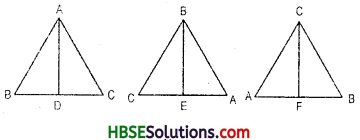
Question 2.
Draw rough sketches of altit udes from A to \(\overline{\mathrm{BC}}\) for the given triangles :

Solution:

Question 3.
Will an altitude always lie in the interior of triangle ? If you think that this need not be true, draw a rough sketch to show such a case.
Solution:
Yes.

Question 4.
Can you think of a triangle in which two altitudes of the triangle are two of its sides ?
Solution:
A triangle has three vertices, and for each vertex there is an altitude. Thus, a triangle has three altitudes. Thus, a triangle in which two altitude of the triangle and two of its sides.

Question 5.
Can the altitude and median be same for a triangle ?
(Hint: For Q. No. 4 and 5, investigate by drawing the altitudes for every type of triangle.)
Solution:
No, the altitude and median arc not same for a tringle.

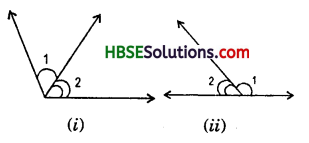
Think, Discuss & Write (Page No. 118):

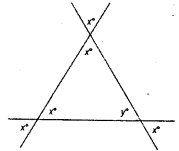
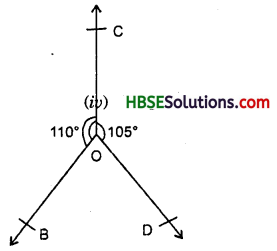
Question 1.
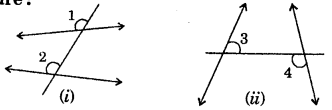
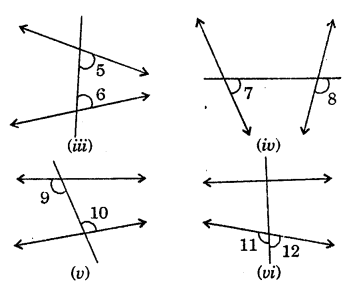
Exterior angles can be formed for a triangle in many ways. Three of them are shown here (fig)

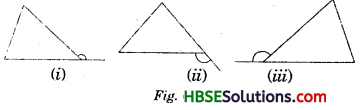
There are three more ways of getting exterior angles. Try to produce those rough sketches.
Solution:
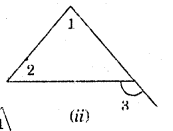
We know that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
i.e. ∠1 + ∠2 = ∠3

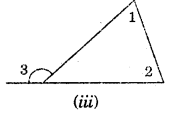
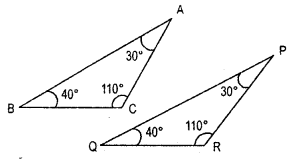
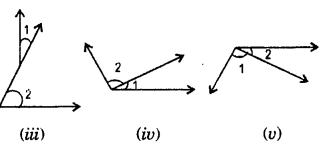
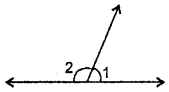
Question 2.
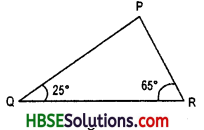
Are the exterior angles formed at each vertex of a triangle equal?
Solution:
(See Fig. ) ∠4 =∠5 (vertically opposite angles )

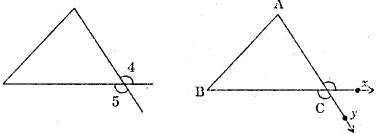
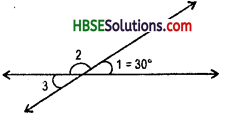
Question 3.
What can you say about the sum of an exterior angle of a triangle and its adjacent interior angle ?
Solution:
∠ACX is called an exterior angle of the ΔABC atC. (Fig. 6.28)
∠ACB is not adjacent ot ∠ACX.
∠ACB is the interior adjacent angle.
∠A and ∠B are not the interior adjacent angles. They are called the interior angles. They are called the interior opposite angles corresponding to exterior angles ∠ACX.
i.e. Sum of an exterior angles and at vertex -C vertically other angles are equal to 360°.

Think, Discuss & Write (Page No. 118):

Question 1.
What can you say about each of the interior opposite angles, when the exterior angles is
(i) a right angle? (ii) an obtuse angle ? (iii) an acute angle.
Solution:
An exterior angle of a triangle is equal to the sum of its interior oppsite singles, (i) a right angle, i.e. (ii) an obtuse angle.

Question 2.
Can the exterior angle of a triangle be a straight angle ?
Solution:
No; because a straight angle = 180°.

Try These (Page No. 118):

Question 1.
An exterior angle of a triangle is of measure 70° and one of its interior opposite angles is of measure 25°. find the measure of the other interior oppsite angle.
Solution:
Let us take m to be the number of
parmit’s marbles other interior opposite angle
= exterior angle — first interior
= oppsite angle
= 70° – 25° = 45°

Question 2.
The two interior opposite angles of an exterior angle of a triangle are 60° and 80°. Find the measure of the exterior angle.
Solution:
Exterior angles = 60° + 80° = 140°.

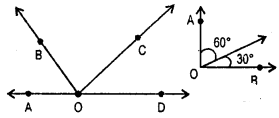
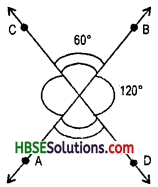
Question 3.
Is something wrong in this diagram (Fig.) ? Comment.
Solution:
We know that,
The sum of interior opposite angles = exterior angles
but from figure,
50 ≠ 50°
Hence this diagram ‘ is wrong.

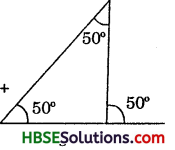
Try These (Page No. 122):

Question 1.
Two angles of a triangle are 30° and 80°.
Find the third angle.
Solution:
By angle – sum property of a triangle
30° + 80° + x° = 180°
110° +x° =180°
∴ x° = 180° – 110° = 70°
∴ third angle = x° = 70°

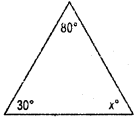
Question 2.
One of the angles of a triangle is 80° and the other two anlges are equal. Find the measure of each of the equal angles.

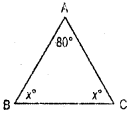
Solution:
By angle – sum property of a triangle
x° + x° + 80° = 180°
or, 2x°+ 80° = 180°
or, 2x° = 180° -80°
= 100°
= \(\frac{100^{\circ}}{2}\) = 50°
angles are 50°, 50°, 80°

Question 3.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.
Solution:
Let the ratio be x :2x:x By angle – sum property of a triangle

x + 2r + x = 180°
or 4x = 180°
or x = \(\frac{180^{\circ}}{4}\) = 45°
∴ angles are 45°, 90°, 45°
Thus the triangles are Right angled and isosceles triangles.

Think, Discuss & Write (Page No. 122):

Question 1.
Can you have a triangle with two right angles ?
Solution:
Since, the three angles of a triangle have a total measure of 180°.
Hence we cannot have a triangle with two right angles.

Question 2.
Can you have a triangle with two obtuse angles ?
Solution:
No, Because obtuse angle > 90°.

Question 3.
Can you have a triangle with two acute angles ?
Solution:
Yes, Because acute angle < 90°.

Question 4.
Can you have a triangle with all the three angles greater than 60° ?
Solution:
No, Because the three angles of a triangle have a total measure of 180°.

Question 5.
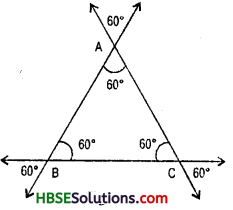
Can you have a triangle with all the three angles equal to 60° ?
Solution:
Yes, Because 60° + 60° + 60° = 180°.

Question 6.
Can you have a triangle with all the three angles less than 60° ?
Solution:
No, Because the three angles of a triangle have a total measure of 180°.

Try These (Page No. 123- 124):

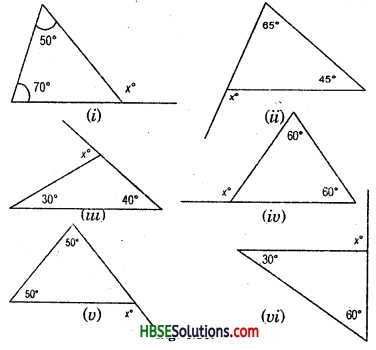
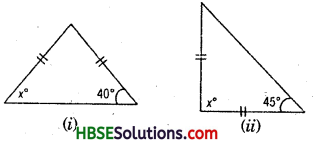
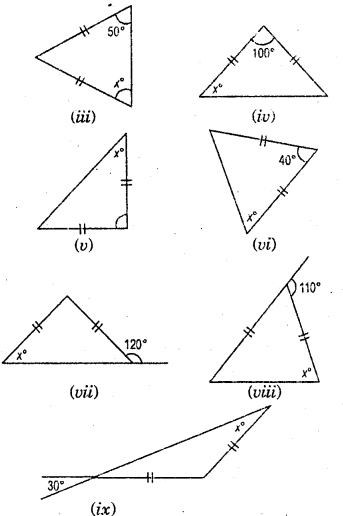
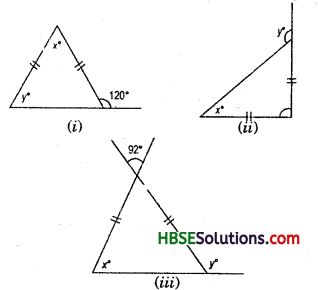
Question 1.
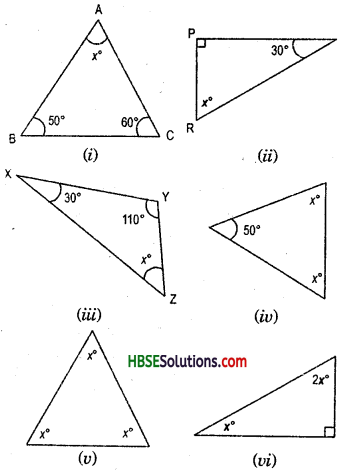
Find angles x in each Fig.


Solution:
In an isosceles triangle
(a) two sides have same length
(b) base angles opposite to the equal sides are equal.
Hence, (i) x° = 40°
(ii) x° + 45° + 45° = 180°
or, x° + 90° = 180°
.’. x° = 180°-90° = 90°

(iii) x° = 50°
(iv) x°+x° + 100° = 180°
2x° = 180°-100° = 80°
x° = \(\frac{80^{\circ}}{2}\) = 40°

(v) x° + x° + 90° = 180°
or, 2x° = 180°-90° = 90°
x° = \(\frac{90^{\circ}}{2}\) = 45°

(vi) x° + x° + 40° = 180°
or, 2x° = 180°-40° = 140°
x° = \(\frac{140^{\circ}}{2}\) = 70°

(vii) x° + 120° = 180° = Linear pair
or, x° = 180°-120°
.. x° = 60°. (Fig. )

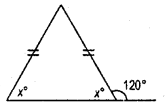
(viii) y° + 110° = Linear pair = 180°
or, y° =180° —110°
y° =70°
Now, x° + x° + y° = 180°
or, 2x° + 70° =180°
2x° =180°-70° = 110°
.’. x = \(\frac{110}{2}\) = 55°

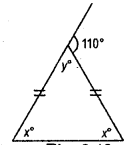
(ix) 30° =30°
= vertically opposite angle
x° =30°,
Because base angles opposite to the equal sides are equal. (Fig.)

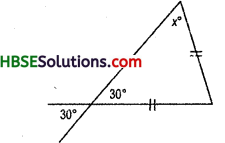
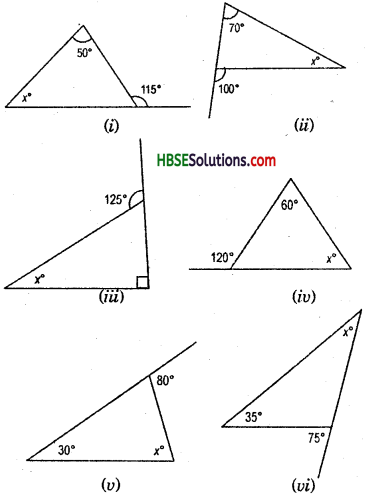
Question 2.
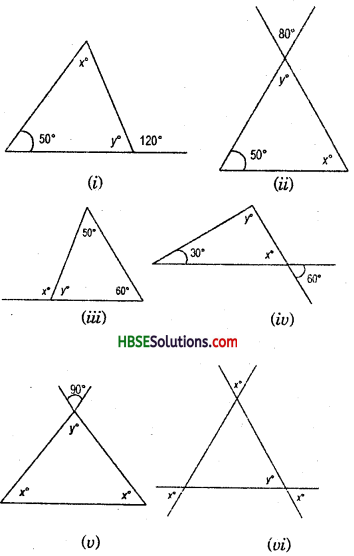
Find angles x andy each Fig.

In isosceles triangle base angled are equal. Hence y° = z°
Solution:
(i) z° + 120° = Linear pair = 180°
∴ z° =180° -120°
∴ z° = 60°
or, x°+y° + 2° = 180° (.-. y° = z°)
x° + 60° + 60° = 180°
or, x° = 180°-120° = 60°
∴ x° = 60°,
y° = 60°

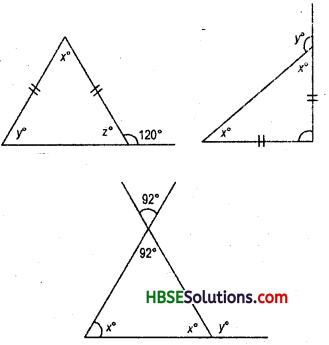
(ii) x° + x° + 90° = 180°
or, 2x° = 180° – 90° = 90°
∴ x° = \(\frac{90}{2}\) = 45°
or, x° + y° = 180° = linear pair
45° +y° = 180°
∴ y° = 180°-45° = 135°
∴ x° = 45°,
y° = 135°

(iii) 92°+ 92° = vertically opposite angle
x° + x° + 92° = 180°
or, 2x° = 180° – 92° = 88°
∴ x = \(\frac{88}{2}\) = 44°
or, x° + y° = linear pair = 180°
44° + y = 180°
y = 180°-44° = 136°
∴ x° = 44°,
y° = 136°.

Think, Discuss & Write (Page No. 127):

Question 1.
Is the sum of any two angles of a triangle always greater than the third angle ?
Solution:
In a triangle, the sum of any two sides of a triangle is always greater than the third side.

Think, Discuss & Write (Page No. 130):

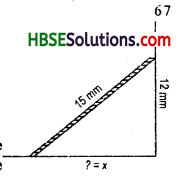
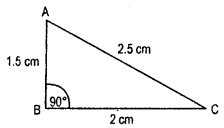
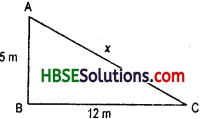
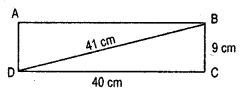
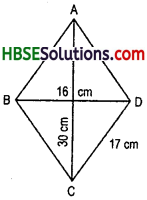
Question 1.
Find the unknown length x in the following figures :

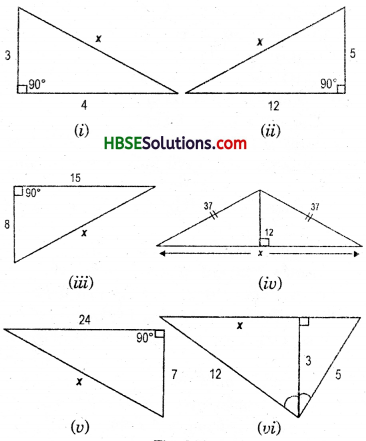
Solution:
By Pythagoras property,
i.e. h² = p² + b²
Hence, (i) x² = 3² + 4²
x² = 9 + 16
x = \(\sqrt{25}\)
∴ x = 5

(ii) x² = (12)² + 5²
∴ x = \(\sqrt{169}\) = 13
∴ x = 13

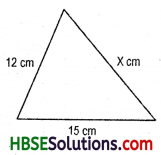
(iii) x² = 8² + 15² = 64 + 225 = 289
∴ x = \(\sqrt{289}\) = 17
∴ x = 17

(iv) x² = 7² + 24² = 49 + 576 = 625
∴ x = \(\sqrt{625}\)
∴ x = 25

(v) h² = p² + b²
In ΔABD, b² = h² – p² = (37)² – (12)²
= 1369-144 = 1225
b = \(\sqrt{1225}\) = 35
= 35 + 35 = 70

(vi) (12)² = 3² + x²
144 – 9 = x²
or, 135 = x²,
∴ x = \(\sqrt{135}\)

Think, Discuss & Write (Page No. 131):

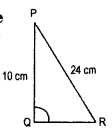
Question 1.
Which is the longest side in the triangle PQR right angled at P ?
Solution:
Longest side = QR.

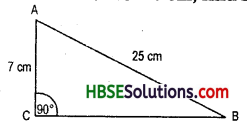
Question 2.
Which is the longest side in the triangle ABC right angled at B ?
Solution:
Longest side = AC.

Question 3.
Which is the longest side of a right triangle?
Solution:
Hypotenuse is the longest side of a right triangle.

Question 4.
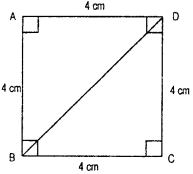
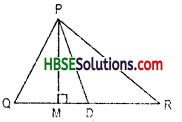
“The diagonal of a rectangle produce by itself the same area as produced by its length and breadth”-This is Baudhayan theorem and Compare it with the Pythagorean property.
Solution:

Pythagoras, a Greek philospher of sixth century B.C. is A B said to have found a very important and useful property of right angled triangles. The Indian Mathemetician Baudhayan has also given an equivalent form of this property.
By Pythagoras property, In a right angle triangle,
The square on the hypotenuse = Sum of the squares on the legs.
i.e. h² = p² + b²
From above figure,
(BD)² = (BC)² + (CD)²
i.e. h² – p² + b²
This is Baudhayan Theorem.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.5

Question 1.
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Solution:

(PR)² = (PQ)² + (QR)²
⇒ (QR)² =(PR)² – (PQ)²
= (24)²-(10)²
= 576 – 100 = 476
∴ QR = \(\sqrt{476}\)
= \(\sqrt{2 \times 2 \times 7 \times 17}=\sqrt[2]{119}\)

Question 2.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.

Solution:
(AB)² = (AC)² + (BC)²
(25)² = 7² + (BC)²
625-49 = (BC)²
576 = (BC)²
\(\sqrt{576}\) =, BC
24 = BC
∴  BC = 24 cm.

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance (Fig. 6.56). Find the distance of the foot of the ladder from the wall.
Solution:

Let ? = x
(15)² = (12)² + x²
225 -144 = x²
81 = x²
\(\sqrt{81}\) = x
9 = x
∴  x = 9
The distance of the foot of the ladder from the wall = 9mm.

Question 4.
Which of the following can be the sides of a right triangle ?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right angled triangles, identify the right angles.
Solution:

In a right triangle
h² = p² + b²
(iii) (1.5 cm, 2 cm, 2.5 cm) is the right angle
h² = p² + b²
(2.5)² = (1.5)² + (2)²
6.25 = 2.25 + 4
6.25 = 6.25
This is satisfied.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:

Let the original height of tree = x
∴  x² = (5)² + (12)²
= 25 + 144 = 169
∴  x = \(\sqrt{169}\)
∴ The original height of the tree = 13 m.

Question 6.
Angle Q and R of a APQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²

Solution:
∠QPR = 180° – (25° + 65°)
= 180°-90°
∴  ∠QPR = 90
By Pythagoras Property,
(QR)² = (PR)² + (PQ)²
i.e. h² = p² + b²
hence, QR² = (PQ)² + (RP)² i.e. (ii) is true.

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Solultion:
From Fig 6.88
(BC) = (BD) – (CD)
= (41) – (40)
= 1681 – 1600 = 81
∴  BC = \(\) = 9 cm.
Thus the perimeter of the rectangle
= 2 ( l x b) = 2(40 + 9)
= 2 x 49 = 98 cm.

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:

Area of Rhombus
= \(\frac{1}{2}\) x d₁ x d₂ Sq.units.

(where d₁ and d₂ are diagonals of rhombus) Side of Rhombus (a) = \(\frac{1}{2} \sqrt{\left(d_{1}\right)^{2}+\left(d_{2}\right)^{2}}\)
Perimeter of Rhombus = 4 x a
Here,
d₁ = 16 cm
d₂ = 30 cm
∴  Side of Rhombus (a)
= \(\frac{1}{2} \times \sqrt{(16)^{2}+(30)^{2}}=\frac{1}{2} \times \sqrt{256 \times 900}\)
= \(\frac{1}{2}\) x \(\sqrt{(16)^{2}+(30)^{2}}\) = \(\frac{1}{2}\) x 34 =17 cm z z
∴ Perimeter of Rhombuse
= 4 x a = 4 x 17= 68
∴ Perimeter of Rhombus = 68 cm.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.4 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.4

Question 1.
Is it possible to have a triangle with the following sides.
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:
(i) 2 cm, 3 cm, 5 cm
∵ 2 cm + 3 cm = 5 cm
and third side = 5 cm
∴ Sum of the measure of lengths of two sides = length of third side which is not possible.
∴ A triangle cannot be possible with these sides.

(ii) 3 cm, 6 cm, 7 cm
∵ 3 cm + 6 cm = 9 cm and 9 cm > 7 cm
3 cm + 7 cm = 10 cm and 10 cm > 6 cm
6 cm + 7 cm = 13 cm and 13 cm > 3 cm
Thus, a triangle can be possible with these sides.

(iii) 6 cm, 3 cm, 2 cm
∵ 6 cm + 3 cm = 9 cm and 9 cm > 2 cm
3 cm + 2 cm = 5 cm and 5 cm < 6 cm
2 cm + 6 cm = 8 cm and 8 cm > 5 cm
∴ A triangle cannot be possible with these sides.

Question 2.
Take any point O in the interior of a triangle PQR. Is
(i) OP + PQ > OQ ?
(ii) OQ + OR > QR ?
(iii) OR + OP > RP ?

Solution:
Sum of the lengths of any two sides of a triangle is greater than the length of than the length of the third side. (Fig. 6.47)
(i) Yes (ii) Yes (iii) Yes

Question 3.
AM is a median of a triangle ABC. Is AB + BC + CA + > 2 AM ?
Solution:
Since the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

∴ In ΔABM, we have AB + BM > AM ..,(i)
Similarly in AACM, CA + CM > AM …(ii)
Adding (i) and (ii), we have (AB + BM) + (CA + CM) > AM + AM
⇒ [AB + (BM + CM) + CA] > 2AM
⇒ [AB + BC + CA] > 2AM

Question 4.
ΔBCD is quadrialteral. Is AB + BC + CD + DA > AC + BD ?
Solution:
In ΔABC, AB + BC > AC …(i)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

In ΔACD, CD + DA > AC …(ii)
Adding (i) and (ii), we have
AB + BC + CD + DA > AC + AC …(iii)
In ΔABD, AB + DA > BD …(to)
In ΔBCD, BC + CD > BD …(v)
Adding (iv) and (v), we get
AB + BC + CD + DA > BD + BD …(vi)
Adding (iii) and (vi)
2 (AB + BC + CD + DA) > 2(AC + BD)
AB + BC + CD + DA > AC + BD.

Question 5.
ABCD is quadrilateral. Is AB + BC + CD + DA + < 2 (AC + BD) ?
Solution:
In ΔOAB
OA + OB > AB …(i)
[Sum of the lengths of any two sides of a triangle is greater than the length of the third side]
In ΔOBC, OB + OC > BC …(ii)

In ΔOCD, OC + OD > DC …(Hi)
In ΔOAD, OA + OD > AD …(iv)
Adding (i), (ii), (iii) and (iv)
2(OA + OB + OC + OD) > AB + BC + CD + DA
⇒ AB + BC + CD + DA < 2(OA + OB + OC + OD)
⇒ AB + BC + CD + DA < 2(OA + OC + OB + OD)
AB + BC + CD + DA < 2(AC + BD).

Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall ?

Solution:
If x cm be the length of third side, we should have
12 + 15 > x ⇒ 27 > x
x + 12 > 15 ⇒ x > 3
and x + 15 > 12 ⇒ x > – 3
The numbers between 3 and 27 satisfy these.
∴ The length of the third side could be any length between 3 cm and 27 cm.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.3

Question 1.
Find the value of the unknown x in the following diagrams :

Solution:
By angle – sum’property of triangle,
(i) ∠A + ∠B + ∠C = 180°
or, x° + 50° + 60° = 180°
or, x° + 110 = 180°
or, x° = 180°-110°
∴ x° = 70°.

(ii) ∠P + ∠Q + ∠R = 180°
or, 90° + 30° + x° = 1800
or, 120 + x° = 180°.
∴ x° = 180° -120° = 60°.

(iii) ∠X + ∠Y + ∠Z = 180°
or, 30° + 110° + x° = 180°
or, 140 + x° = 180°.
∴ x° = 180°-140° = 40°

(iv) y x° +x° + 50° = 180°
or, 2x°+ 50° = 180°
or, 2x° = 180° – 50° = 130°
∴ x° = \(\frac{130}{2}\) = 65°

(v) x° + x° + x° = 180°
or, 3x° = 180°
∴ x° = \(\frac{180}{3}\) = 60°.

(vi) x° + 2x° + 90° 180°
or, 3x° = 180°-90° = 90°
∴ x° = \(\frac{90}{3}\) = 30°. 3

Question 2.
Find the values of the unknowns x and y in the following diagrams:

Solution:
By angle – sum property of a triangle the three angles of a triangle have a total measure of 180°.
The external angle of a triangle is equal to the sum of of its interior opposite angles and the linear pair = 180°.

(i) x° + 50° = 120°
x° = 120°-50° = 70°
Now, x° + y° + 30° = 180°
or, 70° + y° + 30° = 180°
or y° = 180°-70° = 30°
= 180° -100° = 80°.
x° = 70° , y° = 80°.

ii) y° = 80° vertically opposite angles
Now, x° + y° + 50° = 180°
or, x° + 80° + 50° = 180°
or, x° + 130° = 180°
∴ x° = 180° -130° = 50°
∴ x° = 50°, y° = 80°.

(iii) x° = 50° + 60° = 110°
or, y° + 50° + 60° = 180°
or, y° + 110° = 180°
∴ y°= 180° -110° = 70°
∴ x° = 110°, y° = 70°.

(iv) x° = 60° = vertically opposite angles
Now, x°+y° + 30° = 180°
60° +y° + 30° = 180°
y° + 90° = 180°
∴ y° = 180°-90° = 90°
∴ x° = 60°, y° = 90°.

(v) y° = 90° = = vertically opposite angle
Now, x° + x° +y° = 180°
or, 2x°+ 90° = 180°
or, 2x° = 180°-90° = 90°
∴ x° = \(\frac{90}{2}\) = 45°
∴ angle are, 45°, 45°, 90°.

(vi) x° = x° = vertically opposite angles
Now, x° = y° = vertically opposite angles
∴ x° + x° + x° = 180°

or, 3x° = 180°
∴ x° = \(\frac{180}{3}\) = 60°
∴ x° = 60°,
∴ x° = 60°,
y° = 60°.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.2

Question 1.
Find the value of the unknown exterior angle x in the following diagrams:

Solution:
Since the external angle of a traingle is equal to the sum of the sum of its interior opposite angles. Hence
(i) x° = ∠50° + ∠70° = ∠120°
(ii) x° = ∠65° + ∠45° = 110°
(iii) x° = ∠30° + ∠40° = 70°
(iv) x° = ∠60° + ∠60° = 120°
(v) x° = ∠50° + ∠50° = 100°
(vi) x° = ∠30° + ∠60° = 90°.

Question 2.
find the value of the unknown interior angle x in the following diagrams:

Solution:
external angle = sum of interior angle
(i) Hence 115° = angle x° + 50°
or, 115°-50° = x°
65° = x°
∴ x° = 65°.

(ii) 30° + x° = 100°
or, x° = 100°-30
∴ x° = 70°.

(iii) x° + 90° = 125°
or, x° = 125°- 90′
x° = 35°.

(iv) 60° + x° = 120°
or, x° = 120°-60°
∴ x° = 60°.

(v) 30° + x° = 80°
x° = 80° – 30°
∴ x° = 50°.

(vi) x° + 35° = 75°
or, x° = 75° – 35°
∴ x° = 40°

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 The Triangles and Its Properties Exercise 6.1

Question 1.
In ∆PQR, D is the mid point of QR.
\(\overline{\mathrm{PM}}\) is …………
PD is ………….
Is QM = MR ?

Solution:
\(\overline{\mathrm{PM}}\) is the altitude of ∆PQR. PD i Since median is the segment.
hence, QD = DR
But, QM ≠ MR.

Question 2.
Draw rough sketches for the folowing;
(a) In ∆ABC, BE is a median.
(b) In ∆PQR, PQ and PR are altitudes of the triangle.
(c) In ∆XYZ, YL is an altitude in the exterior of th triangle.
Answer:
(a) Hence BE is a median[fig (a)]

(b) In a ∆PQR, PQ and PR are sides of ∆PQR. [Fig. (b)]

(c) YL is the altitude of the triangle. ∆XYZ [Fig. (c)]

Question 3.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
Solution:
The median and altitude of an isosceles triangle can not be same.
In a ∆ABC AD, BE, CF are median but AL, BM and CN are altitude.
Hence O and O’ are the mid point of median and altitude respectively.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 5 Lines and Angles InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 5 Lines and Angles InText Questions

Try These (Page No. 94):

Question 1.
List ten figures around you and identify the acute, obtuse and right angles found in them.
Solution:

Think, Discuss & Write (Page No. 95):

Question 1.
Can two acute angles be complement of each other ?
Solution:
Yes complementary 30° is and acute angle and 60° is also an acute angle.
30° + 60° = 90° (Complementary angle)

Question 2.
Can two obtuse angles be complement of each other ?
Solution:
No obtuse angle > 90°

Question 3.
Can two right angles be complement of each other ?
Solution:
No, one right angle = 90°

Try These (Page No. 95):

Question 1.
Which pairs of following angles are complementary ?
Solution:
(i) and (iv), because complementary angle = 90°.

Question 2.
What is the measure of the complement each of following given angles ?
(i) 45° (ii) 65° (iii) 41° (iv) 54°
Solution:
(i) Let the complement of 45° is re.
∴ x + 45° = 90°
or x = 90° -45° = 45°
∴ Complement of 45° is 45°.

(ii) Let the complement of 65° is x.
∴ x + 65° = 90°
or re = 90° -65° = 25°
∴ The complement of 65° is 25°.

(iii) Let the complement of 41° be m.
∴ m + 41° = 90°
or m = 90° – 41° = 49°
or m = 49°
Thus, the complement of 41° is 49°.

(iv) Let the complement of 54° be x.
∴ x + 54° = 90°
or re = 90° – 54° = 36°
Thus, the complement of 54° is 36°.

Question 1.
The difference in the measures of two complementary angles is 12°. Find the measures of the angles.
Solution:

90° -x = 12°
90° – 12° = x
or 78° = x
∴  x = 78°

Think, Discuss & Write (Page No. 96):

Question 1.
Can two obtuse angles be supplementary ?
Solution:
No, supplementary angle = 180°
obtuse > 90°.

Question 2.
Can two acute angles be supplementary ?
Solution:
Yes, acute angle < 90°

Question 3.
Can two right angles be supplementary ?
Solution:
Yes, right angle
= 90°

Try These (Page No. 97):

Question 1.
Find the supplementary angles in the following given pairs :
Solution:
(i) Measures of the given angles are 110° and 50°.
∵ 110°+ 50° = 160°.
and 160° ≠ 180°
∴ 110° and 50° are not a pair of supplementary angles.

(ii) Measures of the given angles are 105° and 65°.
∵ 105°+ 65° = 170°.
and 170° ≠ 180°
∴ 105° and 65° are not a pair of supplementary angles.

(iii) Measures of the given angles are 50° and 150°.
∵ 50° + 130° = 180°.
∴ 50° and 130° are a pair of supplementary angles.

(iv) Measures of the given angles are 45° and 45°.
∵ 45° + 45° = 90°. and 90° ≠ 180°
∴ 45° and 45° are not a pair of supplementary angles.

Question 1.
What will be the measure of the supplement of each one of the following angles ?
(i) 100° (ii) 90° (iii) 55° (iv) 125°
Solution:
(i) Let the supplementary of 100° be a.
∴ 100° + x = 180°
or x = 180° – 100° = 80°
∴ The measure of the supplement of 100° is 80°.

(ii) Let the supplementary of 90° be x.
∴ x + 90° = 180°
or x = 180°- 90° = 90°
The measure of the supplement of 90° is 90°.

(iii) Let the supplementary of 55° be x.
∴ 55° + x = 180°
or x = 180° -55° = 125°
The supplement of 55° is 125°.

(iv) Let the supplementary of 125° bey.
∴ y + 125° = 180°
or y = 180°-125° = 55°
∴ The supplement of 125° is 55°.

Question 2.
Among two supplementary angles the measure of the larger angle is 44° more than the measure of the smaller. Find their measures.
Solution:
A-t-q, x + x + 44 = 180°
or, 2x + 44 = 180°

2x = 180° – 44°
x = \(\frac{136}{2}\) = 68°
∴ 68°, 112°

Try These (Page No. 97-98):

Question 1.
Are the angles marked 1 and 2 adjacent ? If they are not adjacent.


Solution:
(i) Yes, (ii) Yes, (iii) No, (iv) Yes,
Yes.
(iii) No, because two angles in a plane are said to be adjacent angles, if they have a common vertex, a common arm and the other two arms on opposite sides of the common arm.

Question 2.
In the given figure are the following adjacent angles ?
(a) ∠AOB and ∠BOC
(b) ∠BOD and ∠BOC

Justify your answer.
Solution:
(a) Yes, because they have a common vertex O and a common arm OB.
(b) No, because they are not placed next to each other.

Think, Discuss & Write (Page No. 98):

Question 1.
Can two adjacent angles be supplementary ?
Solution:
Yes, because two adjacent angles form a supplementary.

Question 2.
Can two adjacent angles be complementary ?
Solution:
Y es, because two adjacent angles form a complementary.

Question 3.
Can two obtuse angles be adjacent angles ?
Solution:
Yes, in the figure, ∠BOC and ∠COD are obtuse angles and they are adjacent angles.

Question 4.
Can an acute angle be adjacent to an obtuse angle ?
Solution:
Yes, in the figure, ∠1 and ∠2 are adjacent angles. ∠1 is acute and ∠2 is an obtuse angle.

Think, Discuss & Write (Page No. 99):

Question 1.
Can two acute angles form a linear pair ?
Solution:
No, because acute angle < 90° and linear pair = 180°. Question 2. Can two obtuse angles form a linear pair ? Solution: No, because obtuse angle > 90°
and linear pair = 180°.

Question 2.
Can two right angles form a linear pair ?
Solution:
Yes, because right angle = 90°
and linear pair = 180°.

Try These (Page No. 99):

Question 1.
Check which of the following pairs of angles form a linear pair:
Solution:
(i) Yes,
∵ 140°+ 40° = 180°
∴ The given pair of angles form a linear pair.

(ii) No,
∵ 60° + 60° = 120°
and 120° ≠ 180°.

(iii) No,
∵ 90° + 80° = 170°
and 170° ≠ 180°.

(iv) Yes,
∵ 115°+ 65° = 180°.

Try These (Page No. 101):

Question 1.
In the given figure, if ∠1 = 30°. find ∠2 and ∠3.

Solution:
Since ∠1 + ∠2 = Linear pair = 180°
or, 30° + ∠2 = 180°
or, ∠2 = 180°-30°
∴ ∠2 = 150°
Now, ∠2 + ∠3 = 180°
or, 150° + ∠3 = 180°
or, ∠3 = 180° -150°
∴ ∠3 = 30°
or, ∠1 = ∠2 = vertically opposite angle
∴ 30° = ∠2
∴ ∠2 = 30°

Question 2.
Give an example for vertically opposite angles in your surroundings.

Solution:
Two angles formed by two intersecting lines having common arm are said to be vertically opposite angles.
Hence, ∠COB = ∠AOD = 60°
= vertically opposite angle
and ∠BOD = ∠AOC = 120°
= vertically opposite angles

Try These (Page No. 104):

Question 1.
Find examples from your surround-ings where lines intersect at right angles.
Solution:
(i) A black board, (ii) A table, (iii) A television (iv) A computer.

Question 2.
Find the measures of the angles made by the intersecting lines at the vertices of an equilateral triangle.

Solution:
Vertices, A, B and C. (Fig.)

Question 3.
Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines.
Solution:

Question 4.
If two lines intersect, do they always intersect at right angles ?
Solution:

Try These (Page No. 105):

Question 1.
Suppose Two lines are given. How many transversals can you draw for these lines.

Solution:
Many

Question 2.
If three lines have a transversal, how many points of intersections are there ?
Solution:
Three.

Question 3.
Try to identify a few transversals in your surroundings.
Solution:
Road, Rail, ladder etc.

Try These (Page No. 1.6):

Question 1.
Name the pairs of angles in each Figure.


Solution:
(ii) i.e. < 1 and < 2 are called pairs corresponding angles. [Fig. (i)]
(it) i.e. <3 and < 4 are called pairs of alternate interior angles. [Fig. (ii)]
(iii) i.e. < 5 and < 6 are called pairs of interior angles on the same side of the transversal. [Fig. (iii)]
(iv) i.e. < 7 and < 8 are called pairs of corresponding angles. [Fig.(iv)]
(v) i.e. < 9 and < 8 are called pairs of alternate interior angles. [Fig. (v)]
(vi) i.e. < 11 and < 12 are called linear pairs. [Fig. (vi)]

Try These (Page No. 109):

Question 1.


Solution:
(i) x = 60°
[∵ x and 60° are alternate interior angles]

(ii) ∠y = 55°
[∵ y and 55° are alternate interior angles]

(iii) If two non-parallel lines are intersected by a transversal, then the angle of pairs of alternate interior angles are not equal.
Hence ∠1 = ∠2

(iv) 60° + z = 180°
⇒ z = 180° – 60°
z = 120°
x = 120°
[ ∵ and 60° are interior angles on the same side of the transversal]
∴ z = 120°.

(v) x = 120°
[∵ x and 120° are corresponding angles]

(vi) a + 60° = 180°
⇒ a = 180° – 60° = 120°
a – c
⇒ c = 120° [alternate angles]
c = b
[vertically opp. angles]
⇒ b = 120° [linear pair]
⇒ b+d = 180°
⇒ 120° + d = 180°
∴ d = 180° – 120° = 60°.

Try These (Page No. 100):

Question 1.


Solution:
(i) Yes, l || m, because alternate interior angles are equal and 50°.
(ii) Yes, l || m, because alternate interior angles are equal and 50°.
(iii) If two parallel lines are intersected by a transversal, then the sum of the interior angles on the same side of the transversal is 180° or supplementary.
Hence, 180° + x = 180°
or, x = 180° -180°
x = 0°
But in this figure one angle is 180°. Hence it is not possible.