Haryana State Board HBSE 7th Class Maths Solutions Chapter 7 Congruence of Triangles Ex 7.2 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 7 Congruence of Triangles Exercise 7.2
Question 1.
Which congruence criterion do you use in the following ?
(a) Given:AC = DF
AB = DF
BC = EF
∴ ΔABC ≅ ΔDEF
![]()
(b) Given : ZX = RP
RQ = ZY
(c) Given:
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
∴ ΔABE ≅ ΔCDB

Solution:
(a) In ΔABC and ΔDEF, we have
AC = DF (given)
AB = DE (given)
BC = EF (given)
Hence, ΔABC ≅ ΔDEF (By SSS congruence Criterion)
![]()
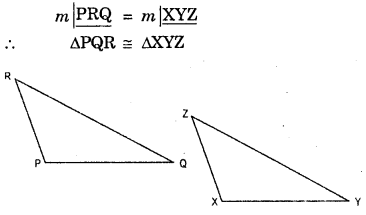
(b) In ΔPQR and ΔXYZ, we have
ZX = RP (given)
RQ = ZY (given)
∠PQR = ∠XYZ (given)
But included angle
∠PQR ≠ ∠XZY
So, SAS congrunce rule cannot be applied and we cannot conclude that the ΔPQR and ΔXYZ are cogruent.
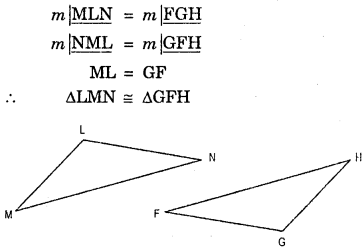
(c) In ΔLMN and ΔGFH, we have
∠MLN = ∠FGH (given)
∠NML = ∠GFH (given) Included side between ∠MLN, ∠NML and ∠FGH, ∠GFH are
ML = GF
Hence ΔLMN ≅ ΔGFH (By ASA congruence Criterion)
(d) In ΔABE and ΔCDB, we have
EB = DB (given)
AE = BC (given)
∠A = ∠C = 90° (given)
i.e. ∠A =∠C = 90°
Side AE = SideBC hypotenuse EB = hypotenuse DB
Hence, ΔABE ≅ ΔCDB (By RHS Congruence Criterion)
Question 2.
You want to show that ΔART ≅ ΔPEN
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(b) If it is given that m∠T = m∠N and you are to use SAS criterion, you need to have
(i) R T =
and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have (i) ? (ii) ?
Solution:
(a) In ΔART and ΔPEN, we have
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
Hence, ΔART ≅ ΔPEN (By SSS congruence rule)
(b) In ΔART and ΔPEN, we have
∠T = ∠N
(i) RT = EN
(ii) AT = PN i.e., PN = AT
Hence, ΔART ≅ ΔPEN (By SAS Congruence Criterion)
(c) In ΔART and ΔPEN, we have
AT = PN
(i) ∠RAT = ∠EPN ⇒ A ⇔ P
(u) ∠RTA = ∠ENP ⇒ T ⇔ T
Hence, ΔART ≅ ΔEPN (By ASA Congruence Criterion)
![]()
Question 3.
You have to show that ΔAMP ≅ ΔAMQ. In the following proof, supply the missing reasons.

Solution:
In ΔAMP Δ AMQ
1. PM = QM ⇒ 1. PM = QM (one side of a right-angled triangle are respectively equal to the one side of another)
2. m∠PMA = m∠QMA ⇒ 2. ∠M = ∠M = 90°
3. AM = AM ⇒ 3. AM = AM = Common
4. ΔAMP ≅ ΔAMQ ⇒ 4. ΔAMP ≅ ΔAMQ (By SAS congruence rule)
Question 4.
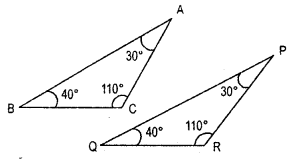
In ΔABC, ∠A = 30° , ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠P = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified ? Why of why not ?
Solution:
In ΔABC and PQR, we have
∠A = ∠P = 30° (given)
∠B = ∠Q = 40° (given)
∠C = ∠R = 110° (given)
Using Angle sum property of triangle
∠A + ∠B + ∠C = 30° + 40° + 110°
= 180°
∠P+ ∠Q + ∠R = 30° + 40° + 110°
= 180°
If AB = PQ, BC = QR and AC = PR,
Hence ΔABC ≅ ΔPQR
(By AAA congruence criterion)
![]()
Question 5.
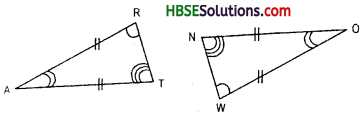
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write. ΔRAT s ?
Solution:
In ΔRAT and ΔWON, we have
RA = WO (given)
AT = ON (given)
included ∠RAT = included ∠WON
Hence ΔRAT ≅ ΔWON
(By SAS congruence rule)
or, In ΔRAT and ΔWON, we have
∠R = ∠W
∠A = ∠O
∠T = ∠N and if RT = WN
Hence ΔRAT ≅ ΔWON (By AAA congruence rule)
Question 6.
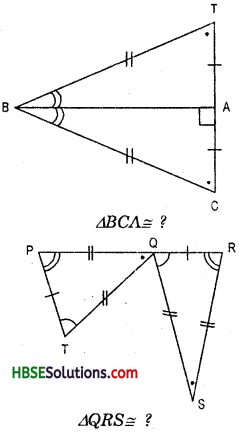
Complete the congruence statement:
Solution:
In ΔTBC
BA is the bisector of base TC
Hence, ∠BAC = ∠BAT = 90°
and AC = AT
Now, In ΔBCA and ΔBTA, we have
∠BAC = ∠BAT =90° (given)
and hypotenuse BC = hypotenuse BT (given)
and Side AC = side AT (given)
BA = BA = Common
Hence, ΔBCA ≅ ΔBTA
(By RHS congruence rule)
or, ΔBCA ≅ ΔBTA
(By SSS congruence rule)
and ; In ΔQRS and QPT, we have
QR = TP (given)
SR = QR (given)
SQ = QT (given)
∠R = ∠P (given)
∠RQS = ∠QTP
and included side QR = TP (given)
Hence, ΔQRS ≅ ΔQPT
(By SSS congruence rule)
and, ΔQRS ≅ ΔQTP
(By ASA congruence rule)
![]()
Question 7.
In a squared sheet, draw two triangles of equal areas such that:
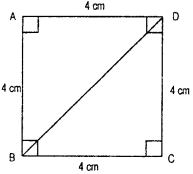
(i) the triangles are congru¬ent.
(ii) the triangles are not con¬gruent.
What can you say answer their perimeters
Solution:
(i) In ΔABD and ΔCBD,
AD = BC = 4 cm (given)
AB = CD = 4 cm (given)
∠A = ∠C = 90° (given)
Hence, ΔABD ≅ ΔCBD (By SAS congruence rule)
(ii) In squared sheet, we have two triangles and two triangles are congrunet.
Hence, two triangles perimeters are equal.
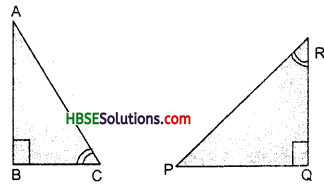
Question 8.
If ΔABC and ΔPQR are to be congruent name one additional pair of corresponding parts. What criterion did you see ?
Solution:
Since ΔABC ≅ ΔPQR
Hence, ∠ABC = ∠RQP = 90°
Hypotenuse AC = Hypotenuse PR
Side AB = Side PQ
So, ΔABC ≅ ΔPQR
(By RHS congruence criterion)
or ∠B = ∠Q = 90
∠C = ∠R
Included side BC = included side QR
Hence ΔABC ≅ ΔPQR
(By ASA congruence criterion)
![]()
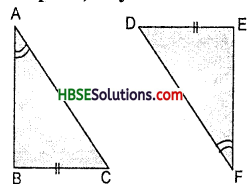
Question 9.
Explain, why ΔABC ΔFED
Solution:
∵ ∠B = ∠E (each 90°)
∠A = ∠F (given)
∠C = ∠D
(third angles are equal) Also BC = ED (given)
Two angles (∠B and ∠C) and included side BC of ΔABC are respectively equal to two angles (∠E and ∠D) and the included side ED of ΔDEF.
∴ ΔABC ≅ ΔFED.