Author name: Prasanna

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 Playing With Numbers InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 Playing With Numbers InText Questions

Try These (Page 58)

Question 1.
Find the possible factors of 45, 30, 36
(i) 45 = 1 × 45
= 3 × 15
= 5 × 9
= 9 × 5
= 15 × 3
= 45 × 1
∴ 1, 3, 5, 9, 15, 45 are all factors of 45.

(ii) 30 = 1 × 30
= 2 × 15
= 3 × 10
= 5 × 6
= 6 × 5
= 10 × 3
= 15 × 2
= 30 × 1
∴ 1, 2, 3, 5, 6, 10, 15, 30 are all factors of 30.

(iii) 36 = 1 × 36
= 2 × 18
= 3 × 12
= 4 × 9
= 6 × 6
∴ 1, 2, 3, 4, 6, 9, 12, 18, 36 are all factors of 36.

Try These (Page 71)

Question 1.
(i) Find the common factors of: (a) 8, 20, (6) 9, 15
Solution:
(a) Factors of 8 :
8 = 1 × 8
= 2 × 4
∴ Factors of 8 are : 1, 2, 4, 8.

Factors of 20 :
20 = 1 × 20
= 2 x 10
= 4 x 5
∴ Factors of 20 are : 1, 2, 4, 5, 10, 20.
Hence, common factors of 8 and 20 are : 1, 2, 4.

(b) Factors of 9 :
9 = 1 × 9
= 3 × 3
∴ Factors of 9 are : 1, 3, 9.

Factors of 15 :
15 = 1 × 15
= 3 × 5
∴ Factor’s of 15 are : 1, 3, 5, 15.
Hence, common factors of 9 and 15 are : 1, 3.

Try These 

Question 1.
Are (i) 7 and 15, (ii) 12 and 49, (iii) 18 and 23 co-prime numbers ?
Solution:
(i) Factors of 7 = 1 × 7
Factors of 7 are : 1, 7.
Factors of 15 = 1 × 15
Factors of 15 are : 1, 3, 5, 15.
= 3 × 5
∴ Common factor of 7 and 15 is 1 only.
Hence, 7 and 15 are co-prime numbers.

(ii) Factors of 12 :
12 = 1x 12
= 2 × 6
= 3 × 4
∴ Factors of 12 are : 1, 2, 3, 4, 6, 12.

Factors of 49 :
49 = 1 x 49
= 7 × 7
∴ Factors of 49 are : 1, 7, 49.
∴ Common factor of 12 and 49 is 1 only.
Hence, 12 and 49 are co-prime numbers.

(iii) Factors of 18 :
18 = 1x 18
= 2 × 9
= 3 × 6
Factors of 18 are : 1, 2, 3, 6, 9, 18.
Factors of 23 = 1 × 23 .
Factors of 23 are : 1, 23.
∴ Common factor of 18 and 23 is only 1.
Hence, 18 and 23 are co-prime numbers.

Try These

Question 1.
Find the common factors of: (a) . 8, 12, 20, (b) 9, 15, 21.
Solution:
(a) 8 = 1 × 8
= 2 x 4

12 = 1 × 12
= 2 × 6
= 3 × 4

20 = 1 × 20
= 2 × 10
= 4 × 5
Factors of 8 are : 1, 2, 4, 8.
Factors of 12 are : 1, 2, 3, 4, 6, 12.
Factors of 20 are : 1, 2, 4, 5, 10, 20.
∴ Common factors of 8, 12, 20 are : 1, 2, 4.

(b) 9 = 1 × 9
= 3 × 3

15 = 1 × 15
= 3 × 5

21 = 1 × 21
= 3 × 7

Factors of 9 are : 1, 3, 9.
Factors of 15 are : 1, 3, 5, 15.
Factors of 21 are : 1, 3, 7, 21.
∴ Common factors of 9, 15, 21 are : 1, 3.

Question 5.
Find the common multiples of:
(a) 4 and 6,
(b) 3, 5 and 6.
Solution:
(a) Multiples of 4 are 4, 8, 12, 16, 20, 24, …………….
Multiples of 6 are 6,12,18,24, 30, 36……….
We observe that 12, 24, 36, are multiples of both 4 and 6.
They are called the common multiples of 4 and 6.

(b) Multiples of 3 are : 3, 6, 9, 12, 15; 18, 21, 24, 27, 30,…………….
Multiples of 5 are : 5, 10, 15, 20, 25, 30, 35, 40, …………….
Multiples of 6 are : 6, 12, 18, 24, 30, 36, 42, 48,…………….
∴ Common multiples of 3, 5 and 6 are 30, 60, 90,…………….

Try These (Page 75)

Question 1.
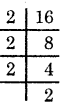
Write the prime factorisations of (i) 16, (ii) 28, (iii) 38.
Solution:
(i) 16 = 2 × 8
= 2 × 2 × 4
= 2 × 2 × 2 × 2

16 = 4 × 4
= 2 × 2 × 4
= 2 × 2 × 2 × 2
In all the above factorisations of 16, we ultimately arrive at only one factorisation 2 × 2 × 2 × 2. In this factorisation the only factor 2 is a prime number. Such a factorisation of a number is called a prime factorisation.
Prime Factorisation Property or The Fundamental Theorem of Arithmetic : “Every number greater than 1 has exactly one prime factorisation.”

(ii) 28 = 2 × 14
= 2 × 2 × 7

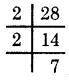
In this factorisation the only factors 2 and 7 are prime numbers.
The prime factorisation of 28 is 2 × 2 × 7.

(iii) 38 = 2 × 19

Here 2 and 19 are both prime numbers
Prime factorisation of 38 is 2 × 19.

Try These (Page 76)

Question 1.
Write the prime factorisations of (a) 8, (b) 12.
Solution:
(a)

∴ Prime factorisation of 8 is 2 × 2 × 2.

(b)

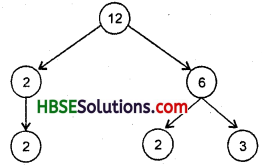
∴ Prime factorisation of 12 is 2 × 2 × 3.

(c)

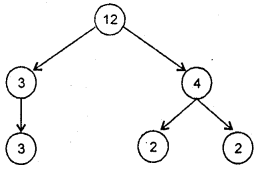
∴ Prime factorisation of 12 is 3 × 2 × 2.

Try These (Page 78)

Question 1.
Find the H.C.F. of
(i) 24 and 36
(ii) 15, 25 and 30
(iii) 8 and, 12
(iv) 12, 16 and 28.
Solution:
(i) 24 = 1 × 24
= 2 × 12 .
= 3 × 8
= 4 × 6

36 = 1 × 36
= 2 × 18
= 3 × 12
= 4 × 9
= 6 × 6
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24 Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
Common factors of 24 and 36 are 1, 2, 3, 4, 6, 12.
Hence, H.C.F. of 24 and 36 is 12.

Another Method :

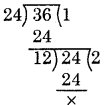
Hence, H.C.F. of 24 and 36 is 12.

(ii) 15 = 1 × 15
= 3 × 5

25 = 1 × 25
= 5 × 5

30 = 1 × 30
= 2 × 15
= 3 × 10
= 5 × 6

∴ Factors of 15 are 1, 3, 5, 15
Factors of 25 are 1, 5, 25
Factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
Common factors of 15, 25 and 30 are 1, 5
Hence H.C.F. of 15, 25 and 30 is 5.

Another Method :

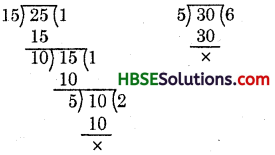
Hence H.C.F. of 15, 25 and 30 is 5.

(iii) 8 = 1 × 8
= 2 × 4

12 = 1 × 12
= 2 × 6
= 3 × 4
∴ Factors of 8 are 1, 2, 4, 8
Factors of 12 are 1, 2, 3, 4, 6, 12
Common factors of 8 and 12 are 1, 2, 4
Hence, H.C.F. of 8 and 12 is 4.

Another Method :

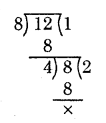
Hence, H.C.F. of 8 and 12 is 4.

(iv) 12 = 1 × 12
= 2 × 6
= 3 × 4

16 = 1 × 16
= 2 × 8
= 4 × 4

28 = 1 × 28
= 2 × 14
= 4 × 7

∴ Factors of 12 are 1, 2, 3, 4, 6, 12
Factors of 16 are 1, 2, 4, 8, 16
Factors of 28 are 1, 2, 4, 7, 14, 28
Common factors of 12, 16 and 28 are 1, 2, 4 .
Hence, H.C.F. of 12, 16 and 28 is 4.

Another Method :

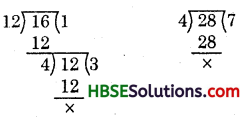
Hence, H.C.F. of 12, 16 and 28 is 4.

Try These (Page 58)

Question 1.
What will be the LCM of: (i) 8 and 12 ? (ii) 4 and 9 ? (iii) 6 and 9 ?
Solution:
(i) Multiples of 8 are : 8, 16, 24, 32, 40, 48, …………..
Multiples of 12 are : 12, 24, 36, 48, 60, 72, ………………
Common multiples of 8 and 12 are : 24, 48, ………………
L.C.M. of 8 and 12 is 24.

Another Method:

(ii) Multiples of 4 are : 4, 8, 12, 16, 20,24, 28, 32, 36, ………………….
Multiples of 9 are : 9, 18, 27, 36, 45, 54, 63, 72, ………………….
Common multiples of 4 and 9 are : 36, 72, ………………….
∴ L.C.M. of 4 and 9 is 36.

Another method :

∴ L.C.M. of 4 and 9 = 2 × 2 × 3 × 3 = 36.

(iii) Multiples of 6 are : 6, 12, 18, 24, 30, 36 , ………………..
Multiples of 9 are : 9, 18, 27, 36, 45, 54, ………………..
Common multiples of 6 and 9 are : 18, 36, ………………..

L.C.M. of 8 and 12 = 2 × 2 × 2 × 3 = 24.

(iii) Multiples of 4 are : 4, 8, 12, 16, 20, 24, 28, 32, 36,
Multiples of 9 are : 9, 18, 27, 36, 45, 54, 63, 72f
Common multiples of 4 and 9 are : 36, 72,

∴ L.C.M. of 6 and 9 = 18.

Another method :

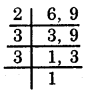
∴ L.C.M. of 6 and 9 = = 2 × 3 × 3 = 18.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions

Try These (Page 86)

Question 1.
With a sharp tip of the pencil mark four points on a paper and name them by the letters A, C, P, H. Try to name these points in different ways. One such way could be this.

Solution:
Other different ways could be :

Try These (Page 87)

Question 1.
Name the line segments in Fig. 4.2. Is A the end point of each line segment ?
Solution:
In Fig., there are two line segments namely \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{AC}}\). Yes, A is the end point of each line segment.

Try These (Page 91)

Question 1.
(i) Name the rays given in this picture.
(ii) Is T a starting point of each of these rays ?

Solution:
(i) In the given Fig. there are three rays, \(\overrightarrow{\mathrm{TA}}, \overrightarrow{\mathrm{TB}}\), and \(\overrightarrow{\mathrm{NB}}\).
(ii) No, T is not the starting point of each of these rays. T is the starting point of two rays \(\overrightarrow{\mathrm{TA}}\) and \(\overrightarrow{\mathrm{TB}}\).

Haryana State Board HBSE 6th Class Maths Solutions Chapter 1 Knowing Our Numbers InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 1 Knowing Our Numbers InText Questions

Try These (Page 2)

Question 1.
Can you instantly find the greatest number in each row and also which is the smallest number ?
1. 387, 4972, 18, 59785, 750
2. 1473,89423, 100, 5000, 310
3. 1834, 75284, 111, 2333, 450
4. 2853,7691,9999, 12002, 1245
Answer:
1. G-59785, S-18.
2. G-89423, S- 100.
3. G-75284, S–111.
4. G-12002, S-124.

Try These (Page 3)

Question 1.
Find the greatest and the smallest number :
(a) 4536, 4892, 4370, 4452.
(b) 15623, 15073, 15189, 15800.
(c) 25286, 25245, 25270, 25210.
(d) 6895, 23787, 24569, 24659.
Answer:
1. G-4892, S-4370.
2. G-15800, S-15073.
3. G-25286, S-25210.
4. G-24659, S-6895.

Try These (Page 3-4)

Question 1.
Use the given digits without repetition and make the greatest and smallest four-digit numbers.
(a) 2, 8, 7, 4 (b) 9, 7, 4, 1
(c) 4, 7, 5, 0 (d) 1, 7, 6, 2,
(e) 5, 4,0,3.
Answer:
(a) G-8742, S-2478.
(b) G-9741, S-1479.
(c) G-7540, S-4057.
(d) G-7621, S-1267.
(e) G-5430, S-3045.

Question 2.
Now make the greatest and the smallest four-digit numbers by using any one digit twice.
(a) 3,8,7
(b) 9, 0, 5
(c) 0,4,9
(d) 8, 5, 1
Answer:
(a) G-8873, S-3378.
(b) G-9950, S-5009.
(c) G-9940, S-4009.
(d) G-8851, S-1158.

Question 3.
Make the greatest and the smallest four-digit numbers using any four different digits, with condition as given
(a) Digit 7 is always at one’s place.
Greatest 9867
Smallest 1027
(b) Digit 4 is always at ten’s place.
Greatest 9847
Smallest 1042
(c) Digit 9 is always at hundred’s place.
Greatest 8976
Smallest 1902
(d) Digit 1 is always at thousand’s place.
Greatest 1987
Smallest 1023

Question 4.
Take two digits, say 2 and 3. From them make four-digit npmbers, using both the digits equal number of times.
(a) Which is the largest number ?
(b) Which is the smallest number ?
(c) How many different numbers can you make in all ?
Answer:
(a) Largest number : 3322
(b) Smallest number : 2233
(c) Different numbers : 3322, 3232, 3223, 2323, 2332, 2233 i.e. 6 in all.

Try These (Page 6)

Question 1.
Arrange the following numbers in ascending order :
(a) 847, 9754, 8320, 571
(b) 9801, 25751, 36501, 38802
Answer:
(a) 571, 847, 8320, 9754
(b) 9801, 25751, 36501, 38802.

Question 2.
Arrange the following numbers in descending order;
(a) 5000, 7500, 85400, 7861
(b) 1971, 45321, 88715, 92547
Answer:
(a) 85400, 7861, 7500, 5000
(b) 92547, 88715, 45321, 1971.

Try These (Page 8)

Question 1.
Read and expand the following numbers :
(i) 50000 (ii) 41000 (iii) 47300 (iv) 57630
(v) 29485 (vi) 29085 (vii) 20085 (iv) 20005.
Answer:

Try These (Page 9)

Question 1.
Read and expand the following numbers :
(i) 4,57,928 (ii) 4,07,928 (iii) 4,00,829 (iv) 4,00,029
Answer:

Try These (Page 10)

Question 1.
What is 10 – 1 = ?
Answer:
9.

Question 2.
What is 100 -.1 = ?
Answer:
99.

Question 3.
What is 10,000 – 1 – ?
Answer:
9999.

Question 4.
What is 1,00,000 – 1 = ?
Answer:
99999.

Question 5.
What is 1,00,00,000 – 1 = ?
Answer:
9999999.

Try These (Page 14)

Question 1.
You have the following digits 4, 5, 6, 0, 7 and 8. Using them make 5 numbers each with 6 digits.
(a) Put commas for ease of reading.
(b) Arrange them in ascending and descending order.
Answer:
(a) 8,76,540; 7,86,540; 6,87,540; 5,78,640; 4,58,760
(b) Ascending order : 4,58,760; 5,78,640; 6,87,540; 7,86,540; 8,76,540
Descending order : 8,76,540; 7,86,540; 6,87,540; 5,78,640; 4,58,760

Question 2.
Take the digits 4, 5, 6, 7, 8 and 9. Make any 3 numbers each with 8 digits. Put commas for ease of reading.
Answer:
4,56,78,469; 5,64,78,965; 6,45,87,695.

Question 3.
From the digits 3, 0 and 4 make 5 numbers each with 6 digits. Use commas.
Answer:
3,04,034; 4,03,403; 3,40,430; 3,03,404; 3,34,400.

Try These (Page 16)

Question 1.
How many centimetres make a kilometre ?
Answer:
1 kilometre (km)
= 1000 x 100 centimetres (cm)
= 1,00,000 cm.

Question 2.
How many milligrams make one kilogram ?
Answer:
1 kilogram
= 1000 x 1000 milligrams (mg)
= 10,00,000 milligrams (mg)

Question 3.
A box of medicine tablets contains 2,00,000 tablets each weighing 20 mg. What is the total weight of all the tablets in the box in grams ? in kilo¬grams ?
Answer:
Total weight of all the tablets
= 20 x 2,00,000 mg
= 40,00,000 mg
= 4,000 g (∵ 1000 mg = 1 g)
= 4kg (∵ 1000 g= lkg)

Kilo shows 1000 times greater,
Milli shows 1000 times smaller,
Centi shows 100 times smaller.

Try These (Page 17)

Question 1.
A bus started its journey and reached different places with a speed of 60 km/hr. The journey is shown below :
(i) Find the total distance covered by the bus from A to D.
(ii) Find the total distance covered by the bus from D to G.

(iii) Find the total distance covered by the bus if it starts from A and returns back to A.
(iv) Can you find the difference of distances from C to D and D to E.
(v) Find out the time taken by bus to reach.
(a) AtoB
(b) C to D
(c) E to G
(d) Total journey.
Solution:
(i) Total distance covered by the bus from A to D
= 4170 km + 3410 km + 2160 km
= 9,740 km.

(ii) Total distance covered by the bus from D to G
= 8140 km + 4830 km + 2550 km
= 15,520 km.

(iii) Total distance covered by the bus
= 9740 km + 15520 km + 1290 km = 26,550 km

(iv) Difference of distances from C to D and D to E
= 8140 km – 2160 km = 5980 km.

(v) (a) A to B = 4170 km, 4170 + 60 = 69% Hrs
(b) C to D = 2160 km,
2160 H- 60 = 36 Hrs
(c) E to G = 4830 km + 2550 km, 7380 + 60 = 123 Hrs
(d) Total journey
= 4170 + 3410 + 2160 + 8140 + 4830 + 2550 + 1290
= 26550 km = 442 1/2 Hrs.

Question 2.

(a) Can you find the total weight of apples and oranges Raman sold last year ?
(b) Can you find the total money Raman got by selling apples ?
(c) Can you find the total money Raman got by selling apples and oranges together ?
(d) Make a table showing how much money Raman received from selling each item. Arrange the entries of amount of money received in decreasing order. Find the item which brought him the highest amount. How much is this amount ?
Solution:
(a) Wt. of apples = 2457 kg
Wt. of oranges = 3004 kg
.’. Total weight = 2457 kg + 3004 kg
= 5461 kg.
(b) Total money got by selling apples = Rs. 40 x 2457
= Rs. 98280.

(c) Total money got by selling apples and oranges together
= Rs. 40 x 2457 + Rs. 30 x 3004 = Rs. 98280 + Rs. 90120 = Rs. 188400.

(d)

Arranging the entries of amount of money in decreasing order :
Rs. 2,53,670; Rs. 2,40,012; Rs. 1,60,040; Rs. 98,280; Rs. 90,120; Rs. 68,280; Rs. 38,530.
Tooth brushes brought him the highest amount which is Rs. 2,53,670.

Try These (Page 23)

Question 1.
Round these numbers to the nearest tens.
28,32,52,41, 39,48,64,59,99,215,1453, 2936
Answer:
(i) 28 is rounded off to 30, correct to the nearest tens.
(ii) 32 is rounded off to 30, correct to the nearest tens.
(iii) 52 is rounded off to 50, correct to the nearest tens.
(iv) 41 is rounded off to 40, correct to the nearest tens.
(v) 39 is rounded off to 40, correct to the nearest tens.
(vi) 48 is rounded off to 50, correct to the nearest tens.
(vii) 64 is rounded off to 60, correct to the nearest tens.
(viii) 59 is rounded off to 60, correct to the nearest tens.
(ix) 99 is rounded off to 100, correct to the nearest tens.
(x) 215 is rounded off to 220, correct to the nearest tens.
(xi) 1453 is rounded off to 1450, correct to the nearest tens.
(xii) 2936 is rounded off to 2940, correct to the nearest tens.

(b) Estimating to the nearest hundreds: Check if the following rounding off to 100
is correct or not. Correct those which are wrong.
(i) 841→ 800 correct
(ii) 9537 → 9500 correct
(iii) 49730 → 49700 correct
(iv) 2546 → 2500 correct
(v) 286 → 300 correct
(vi) 5750 → 5800 correct
(vii) 168 → 200 correct
(viii) 149 → 100 correct
(ix) 9870 → 9800 wrong
→ 9900 correct.

(c) Rounding off to nearest thousands :
Check the following rounding offs. Correct those which are wrong.
(0 2,573 → 3,000 correct
(ii) ‘ 53,552 → 53,000 wrong
→ 54,000 correct
(iii) 6,404 → 6,000 correct
(iv) 65,437 → 65,000 correct
(v) 7,805 → 7,000 → wrong
→ 8,000 correct
(vi) 3,499 → 4,000 wrong
→ 3,000 correct.

Try These (Page 24)

Question 1.
Round off the given numbers to the nearest tens, hundreds and thousands.

Note : There are no rigid rules when you want to estimate the outcotnes on numbers. The procedure depends on the degree of accuracy required, how quickly the estimate is needed and most importantly, how sensible the guessed answer would be.

Try These (Page 28)

Question 1.
Estimate the following products :
(i) 87 x 313
(ii) 9×795
(iii) 898 x 785
(iv) 958 x 387.
Solution:
(i) We try approximating 87 to 90 arid 313 to 300. We get the product 90 x 300 = 27,000 is a quick as well as good estimate of the product.
(ii) We try approximating 9 to 10 and 795 to 800. We get the product 10 x 800 = 8,000 is a quick as well as good estimate of the product.
(iii) We try approximating 898 to 900 and 785 to 800. We get the product 900 x 800 =
7,20,0 is a quick as well as good estimate of the product.
(iv) We try approximating 958 to 1,000 and 387 to 400. We get the product 1,000 x 400 = 4,00,000 is a quick as well as good estimate of the product.

Try These (Page 29)

Question 1.
Write the expressions for each of the following using brackets :
(a) Four multiplied by the sum of nine and two.
(b) Divide difference of eighteen and six by four. ,
(c) Forty five divided by three times of the sum of three and two.
Answer:
(a) 4 x (9 + 2),
(b) (18 – 6) + 4,
(c) 45 ÷ 3(3 + 2).

Question 2.
Write 3 different situations for (5 + 8) x 6.
Answer:
(a) 1st situation: Sohani and Reeta work for 6 days; Sohani works 5 hours a day and Reeta 8 hours a day. How many hours do both of them work in a day ?
(b) Ilnd situation : Suman bought 5 note-books from the market and the cost was Rs. 6 per note-book. Her sister Seema also- bought 8 note-books of the same type. Find the total money they paid.
(c) Illrd situation : Ram covered a
distance of 5 km in one hour and Shyam covered a distance of 8 km in one hour. How much distance did they cover in 6 hours ?

Question 3.
Write 5 such situations for the following where brackets would be necessary.
Answer:
(a) 7 (8 – 3) is 7 times (8 – 3) and so the answer is 7 x 5 = 35.
(b) (7 + 2) (10 – 3) is (9) (7) or 9 x 7 = 63.
(c) 5 (10 – 3) is 5 times (10 – 3) and so the answer is 5 x 7 = 35.
(d) (7 – 2) (10 + 3) is (5) (13) or 5 x 13 = 65.
(e) 18 (5 – 2) is 18 times (5 – 2) and so the answer is 18 x 3 = 54.

Try These (Page 29-30)

1. 7 x (100 + 9)
7 x 100 + 7.x 9 700 + 63 = 763

2.  102 x 103 = (100 + 2) x (100 + 3)
= 100 x 100 + 2 x 100 + 100 x 3 + 2 x 3
= 10,000 + 200 + 300 + 6
= 10,000 + 500 + 6
= 10,506.

3. 17 x 109 = (10 + 7) x (100 + 9)
= 10 x 100 + 7 x 100 + 10 x 9 + 7 x 9
= 1000 + 700 + 90 + 63
= 17790 + 63
= 1853.

Try These (Page 32)

Question 1.
Write in Roman Numerals :
1. 73
2. 92.
Solution:
1. 73 = 70 +3 = (50+ 20)+ 3 = LXX + III = LXXIII
2. 92 = 90 + 2 = (100 – 10) + 2 = XC + II = XCII.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.1

Question 1.
Use the figure to name
(a) 5 points
(b) a line
(c) 4 rays
(d) 5 line segments.
Solution:
(a) 5 points are O, B, C, D and E.
(b) A line is \(\) or \(\).
(c) 4 rays are \(\) and \(\).
(d) 5 line segments are \(\overline{\mathrm{OB}}, \overline{\mathrm{OC}}, \overline{\mathrm{OF}}, \overline{\mathrm{OD}},\overline{\mathrm{DE}}\).

Question 2.
Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.
Solution:
Possible twelve names are as follows:

Question 3.
Name :
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which 0 lies.
(d) Two pairs of intersecting lines.

Solution:
(a) Line containing point E is \(\overleftrightarrow{\mathrm{EF}}\)
(b) Line passing through A is \(\overleftrightarrow{\mathrm{AE}}\).
(c) Line on which O lies is \(\overleftrightarrow{\mathrm{OC}}\)
(d) Two pairs of intersecting lines are : \(\stackrel{\leftrightarrow}{\mathrm{AE}}, \overleftrightarrow{\mathrm{OC}}\) and \(\stackrel{\leftrightarrow}{\mathrm{AE}}, \overleftrightarrow{\mathrm{EF}}\)

Question 4.
How many lines can pass through :
(a) one given point ?
(b) two given points ?
Solution:
(a) Infinite number of lines can pass through one given point.
(b) Only one line can pass through two given points.

Question 5.
Draw a rough figure and label suitably in each of the following cases :
(a) Point P lies on \(\overline{A B}\) .
(b) XY and PQ intersect at M.
(c) Line l contains E and F but not D.
(d) OP and OQ meet at O.
Solution:

Question 6.
Consider the following figure of line MN. Say whether following state¬ments are true or false in context of given figure.
(a) Q, M, O, N, P are points on the line MN.
(b) M, O, N are points on a line segment . \(\overline{M N}\).
(c) M and N are end points of line segment \(\overline{M N}\).
(d) 0 and N are end points of line segment \(\overline{OP}\).
(e) M is one of the end points of line segment \(\overline{QO}\).
(f) M is point on ray \(\overrightarrow{OP}\).
(g) Ray \(\overrightarrow{OP}\) is different from ray \(\overrightarrow{QP}\).
(h) Ray \(\overrightarrow{OP}\) is same as ray \(\overrightarrow{OM}\).
(i) Ray \(\overrightarrow{OM}\) is not opposite to ray \(\overrightarrow{OP}\).
(j) 0 is not an initial point of \(\overrightarrow{OP}\).
(k) N is the initial point of \(\overrightarrow{NP}\) and \(\overrightarrow{N M}\).
Solution:
(a) True,
(b) True,
(c) True,
(d) False,
(e) False,
(f) False,
(g) False,
(h) True,
(i) False,
(j) False,
(k) True.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 2 Whole Numbers InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 2 Whole Numbers InText Questions

Try These (Page 34)

Question 1.
Write the predecessor and successor of : 19; 1,997; 12,000; 49; 1,00,000; 24,40,701; 1,00,199; 2,08,090.
Answer:

Question 2.
Is there any natural number that has no predecessor ?
Answer:
Yes, 1 has no predecessor.

Question 3.
Is there any natural number which has no successor ?
Is there a last natural number ?
Answer:
No, every natural number has a successor.
No, there is no last natural number.

Try These (Page 35)

Question 1.
Are all natural numbers also whole numbers ?
Answer:
Yes, all natural numbers are also whole numbers.

Question 2.
Are all whole numbers also natural numbers ?
Answer:
No, ‘0’ is a whole number but not a natural number.

Question 3.
Which is the smallest whole number ?
Answer:
‘0’ is the smallest whole number.

Question 4.
Which is the greatest whole number ?
Answer:
There is no greatest whole number.

Try These (Page 37)

Question 1.
Find 4 +5; 2 +6; 3 +5; 1 + 6 using the number line.
Answer:
(a) 4 + 5

The point at the tip of the arrow is 4. Start at 4.
Since, we add 5 to this number so we make 5 jumps to the right; from 4 to 5, 5 to 6, 6 to 7, 7 to 8 and 8 to 9 as shown above in Fig. The tip of the last arrow in the fifth jump is at 9.
∴ The sum of 4 and 5 is 9 i.e. 4 + 5 = 9.

(b) 2 + 6

The point at the tip of the arrow is 2. Start at 2.
Since we add 6 to this number so we make 6 jumps to the right; from 2 to 3, 3 to 4, 4 to 5, 5 to 6, 6 to 7 and 7 to 8 as shown above in Fig. 2.2. The tip of the last arrow in the sixth jump is at 8.
∴ The sum of 2 and 6 is 8 i.e., 2 + 6 = 8.

(c) 3 + 5

The point at the tip of the arrow is 3. Start at 3. Since we add 5 to this number so we make 5 jumps to the right; from 3 to 4, 4 to 5, 5 to 6, 6 to 7 and 7 to 8 as shown above in Fig. 2.3. The tip of the last arrow in the fifth jump is at 8.
∴ The sum of 3 and 5 is 8 i.e., 3 + 5 = 8.

(d) 1 + 6

The point at the tip of the arrow is 1. Start at 1. Since we add 6 to this number so we make 6 jumps to the right; from 1 to 2, 2 to 3, 3 to 4, 4 to 5, 5 to 6 and 6 to 7 as shown in Fig. 2.4 above. The tip of the last arrow in the sixth jump is at 7.
∴ The sum of 1 and 6 is 7 i.e., 1 + 6 = 7.

Try These (Page 37)

Question 1.
Find 8-3; 6-2; 9-6 using the number line.
Answer:
(a) 8-3.

The point at the tip of the arrow is 8. Start from 8. Since 3 is being subtracted, so move towards left with 1 jump of 1 unit. Make 3 such jumps. We reach at the point 5.
∴ We get 8 – 3 = 5.

(b) 6 – 2

The point at the tip of the arrow is 6. Start from 6. Since 2 is being subtracted, so move towards left with 1 jump of 1 unit. Make 2 such jumps. We reach at the point 4.
∴ We get 6-2 = 4.

(c) 9-6.

The point at the tip of the arrow is 9. Start from 9. Since 6 is being subtracted, so move
towards left with 1 jump of 1 unit. Make 6 such jumps. We reach at the point 3.
∴ We get 9 – 6 = 3.

Try These (Page 37)

Question 1.
Find 2 x 6; 3 x 3; 4 x 2 using number line.
Answer:
(a) Let us find 2 x 6.

Start from ‘0’, move 2 units at a time to the right. Make 6 such moves. We reach at 12. So, we say 2 × 6 = 12.

(b) 3 x 3.

Start from ‘0’, move 3 units at a time to the right. Make such 3 moves, we reach at 9. So, we say 3 × 3 = 9.

(c) 4 × 2.

Start from ‘0’, move 4 units at a time to the right. Make such 2 moves, we reach at 8. So, we say 4 x 2 = 8.

Try These (Page 45)

Question 1.
(i) 7 + 18 + 13 (ii) 16 + 12 + 4.
Solution:
(i) 7 + 18 + 13 = (7 + 13) + 18
= 20 + 18 = 38
(ii) 16 + 12 + 4 = (16 + 4) + 12
= 20 + 12 = 32.

Question 2.
(i) 25 × 8358 × 4
(ii) 625 × 3759 × 8.
Solution:
(i) 25 × 8358 × 4
= (25 × 4) × 8358
= 100 × 8358
= 835800

(ii) 625 × 3759 × 8
= (625 × 8) × 3759
= 5000 × 3759
= 18795000

Question 3.
(i) (16 ÷ 4) ÷ 2 and 16 ÷ (4 ÷ 2)
(ii) (28 ÷ 14) ÷ 2 and 28 ÷ (14 ÷ 2).
Solution:
(i)( 16 ÷ 4) ÷ 2= 4 ÷ 2 = 2
and 16 ÷ (4 ÷ 2) = 16 ÷ 2 = 8
.-. (16 ÷ 4) ÷ 2 ≠ 16 ÷ (4 ÷ 2)
(ii) (28 + 14) ÷ 2 = 2 ÷ 2 = 1
and 28 ÷ (14 ÷ 2) = 28 ÷ 7 = 4
.-. (28 ÷ 14) ÷ 2 ≠ 28 + (14 ÷ 2)
Hence there is no associative property for division.

Try These (Page 48)

Question 1.
(i) 15 × 68
(ii) 17 × 23
(iii) 69 × 78 + 22 × 69.
Solution:
(i) 15 × 68 = 15 × (60 + 8)
= 15 × 60+ 15 × 8 = 900 + 120 = 1020
(ii) 17 × 23 = 17 × (20 + 3)
= 17 × 20 + 17 × 3 = 340 + 51 = 391
(iii) 69 × 78 + 22 × 69
= (78 + 22) × 69 = 100 × 69 = 6900

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.6 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.6

Question 1.
From Fig., identify
(a) the centre of the circle
(b) three radii
(c) a diameter
(d) a chord

(e) two points in the interior
(f) a point in the exterior
(g) a sector
(h) a segment.
Solution:
(a) Point O is the centre of the circle.
(b) Line segments \(\overline{\mathrm{OA}}, \overline{\mathrm{OB}}\) and \(\overline{\mathrm{OP}}\) are three radii of the circle.
(c) Line segment \(\overline{\mathrm{AC}}\) is a diameter of the circle.
(d) Line segment \(\overline{\mathrm{ED}}\) is a chord of the circle.
(e) Points 0 and P are in the interior of the circle.
(f) Point Q is in the exterior of the circle.
(g) The shaded portion OAB is a sector of the circle.
(h) The shaded part of chord ED is a segment.

Question 2.
(a) Is every diameter of a circle also a chord ?
(b) Is every chord of a circle also a diameter ?
Solution:
(a) Yes, every diameter of a circle is also a chord of the circle.
(b) No, every chord of a circle is not a diameter of the circle.

Question 3.
Draw any circle and mark
(a) its centre
(b) a radius
(c) a diameter
(d) a sector
(e) a segment
(f) a point in its interior
(g) a point, in its exterior
(h) an arc.
Solution:
(a) Point C is the centre of the circle.
(b) Line segment \(\overline{\mathrm{CP}}\) is its radius.

(c) Line segment \(\overline{\mathrm{QCP}}\) is its diameter.
(d.) The shaded region ACP is a sector.
(e) The dark-shaded region ABQ is a segment.
(f) Point D is in the interior of the circle.
(g) Point E is in the exterior of the circle.
(h) \(\overparen{Q B A}\) is an arc of the circle.

Question 4.
Say true or false :
(a) Two diameters of a circle will necessarily intersect,
(b) The centre of a circle is always in its interior.
Solution:
(a) True, (b) True.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.5

Question 1.
Draw a rough sketch of a quadri-lateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral ?
Solution:
Two diagonals are PR and QS. The meeting point of the diagonals is in the interior of the quadrilateral.

Question 2.
Draw a rough sketch of a quadri-lateral KLMN. State :
(i) two pairs of opposite sides.
(ii) two pairs of opposite angles.
(Hi) two pairs of adjacent sides.
(iv) two pairs of adjacent angles.
Solution:
(i) Two pairs of opposite sides are : KL, MN and LM, KN. .
(ii) Two pairs of opposite angles are : ∠K, ∠M and ∠L, ∠N.

(iii) Two pairs of adjacent sides are : KL, LM and LM, MN.
(iv) Two pairs of adjacent angles are: ∠K, ∠L and ∠L, ∠M.

Question 3.
Investigate: Use strips and fasten to make a triangle and a quadri-lateral. Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral. Is the triangle dis-torted ? Is the quadrilateral distorted ? Is the triangle rigid ? Why is it that structures like electric towers make use of triangular shapes and not quadri-laterals ?
Solution:
No, triangle is not distorted. Yes, quadrilateral is distorted. Yes, the triangle is rigid. Because triangular shape is not affected.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.4

Question 1.
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its interior or in its exterior ?
Solution:
Point A is neither in the interior nor in the exterior of the triangle, but it is on the ΔABC.

Question 2.
Identify three triangles in Fig. Write the names of seven angles. Write the names of six line segments. Which two triangles have ∠B as common ?
Solution:

In Fig., three triangles are, ΔABC, ΔABD and ΔACD.
Seven angles are : ∠BAD, ∠ADB, ∠ABD, ∠DAC, ∠ACD, ∠ADC and ∠BAC.
Six line-segments are : AB, BC, CA, AD, BD and CD.
ΔABD and ΔABC have ∠B as common.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.3

Question 1.
Name the angles in the given fig.

Solution:
(i) ∠ABC
(ii) ∠BCD.
(iii) ∠CDA.
(iv) ∠DAB

Question 2.
In the given Fig. , name the point(s)

(а) In the interior of ∠DOE.
(b) In the exterior of ∠EOF.
(c) On ∠EOF.
Solution:
(a) Point A is in the interior of ∠DOE.
(b) Point C and A are in the exterior of ∠EOF.
(c) Point B is on ∠EOF

Question 3.
Draw rough diagrams of two angles such that they have
(а) One point in common.
(b) Two points in common.
(c) Three points in common.
(d) Four points in common.
(e) One ray in common.

Solution:
(a) O is common to both the angles ∠AOC and ∠BOC.
(b), (c), (d) are not possible.
(e) \(\overrightarrow{\mathrm{OC}}\) is one ray common to both angles ∠AOB and ∠BOC.

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas Exercise 4.2

Question 1.
Classify the following curves as (i) open or (ii) closed.

Solution:
Curves (a) and (c) are open curves and (b), (d) and (e) are closed curves.

Question 2.
Draw rough diagrams to illustrate the following :
(a) Open curve (b) Closed curve.
Solution:

Question 3.
Draw any polygon and shade its terior.
Solution:

Question 4.
Consider the given Fig., and answer the questions :

(a) Is it a curve ?
(b) Is it closed. ?
(c) Is it a polygon ?
Solution:
(a) Yes, it is a curve.
(b) Yes, it is closed.
(c) Yes, it is a polygon.

Question 5.
Illustrate, if possible, each of the following with a rough diagram :
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.

Solution:
(c) A polygon with two sides is not possible