Haryana State Board HBSE 6th Class Maths Solutions Chapter 12 Ratio and Proportion Intext Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 12 Ratio and Proportion Intext Questions
TRY THESE (Page 323)
Question 1.
In a class there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls ?
Solution:
Number of boys = 20
Number of girls = 40
∴ Ratio between the number of boys and the number of girls = \(\frac{20}{40}=\frac{1}{2}\) = 1 : 2.
![]()
Question 2.
Ravi walks 6 km in an hour while Roshan walks 4 km in an houF. What is the ratio of the distance covered by Ravi to the distance covered by Roshan ?
Solution:
Distance covered by Ravi = 6 km
Distance covered by Roshan = 4 km
∴ Ratio of the distance covered by Ravi to the distance covered by Roshan
= \(\frac{6 \mathrm{~km}}{4 \mathrm{~km}}=\frac{3}{2}\) = 3 : 2
TRY THESE (Page 325)
Question 1.
Saurabh takes 15 minutes to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin.
Solution:
Time taken by Saurabh = 15 minutes Time taken by Sachin
= 1 hour = 60 minutes
∴ Ratio of the time taken by Saurabh to the time taken by Sachin
\(\frac{15 \text { minutes }}{60 \text { minutes }}=\frac{1}{4}\)
= 1:4.
Question 2.
Cost of a toffee is 50 paise and cost of a chocolate is Rs. 10. Find the ratio of the cost of a toffee to the cost of a chocolate.
Solution:
Cost of a toffee = 50 paise
Cost of a chocolate
= Rs. 10 = 10 x 100
= 1000 paise
∴ Ratio of the cost of a toffee to the cost of a chocolate
\(\frac{50 \text { paise }}{1000 \text { paise }}=\frac{1}{20}\)
= 1: 20.
![]()
Question 3.
In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year ?
Solution:
Number of holidays in the year = 73
Number of days in one year = 365
∴ Ratio of the number of holidays to the number of days in one year
= \(\frac{73}{365}=\frac{1}{5}\) = 1:5.
TRY THESE (Page 336)
(Check whether the given ratios are equal i.e., they are in proportion. If yes, then write them in proper form.
1. 1 : 5 and 3 : 15
2. 2:9 and 18 : 81
3. 15 : 45 and 5 : 25
4. 4 : 12 and 9 : 27
5. Rs. 10 to Rs. 15 and 4 to 6.
Solution:
1. 1 : 5 = \(\frac{1}{5}\) and 3 : 15 = \(\frac{3}{15}=\frac{1}{5}\)
Here, the two ratios 1 : 5 and 3 : 15 are equal.
1. e., they are in proportion
∴ 1 : 5 :: 3 : 15.
2. 2:9 = \(\frac{2}{9}\) and 18:81 = \(\frac{18}{81}=\frac{2}{9}\)
Here, the two ratios 2 : 9 and 18 : 81 are equal.
i.e., they are in proportion.
∴ 2 : 9 :: 18 : 81.
3. 15:45= \(\frac{15}{45}=\frac{1}{3}\) and 5 : 25 = \(\frac{5}{25}=\frac{1}{5}\)
Here the two ratios 15 : 45 and 5 : 25 are not equal.
i.e., 15 : 45 * 5 : 25.
∴ They are not in proportion.
4. 4 : 12 = \(\frac{4}{12}=\frac{1}{3}\) and 9 : 27 = \(\frac{9}{27}=\frac{1}{3}\)
Here the two ratios 4 : 12 and 9 : 27 are equal.
i.e. they are in proportion.
∴ 4 : 12 :: 9 : 27.
![]()
5. Ratio of Rs. 10 to Rs. 15 = \(\frac{10}{15}=\frac{2}{3}\) and 4:6 = \(\frac{4}{6}=\frac{2}{3}\)
Here the two ratios are equal.
i.e. they are in proportion.
∴ Rs. 10 : Rs. 15 :: 4 : 6.
“In a statement of proportion, the four quantities involved are also known as respective terms. First and fourth terms are known as extreme terms. Second and third terms are known as middle terms.”
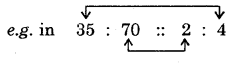
35, 70, 2, 4 are respective terms. 35 and 4 are extreme terms and 70 and 2 are middle terms.
Remember that, in a proportion
Product of extreme terms
= Product of middle terms
Here, product of extreme terms = 35 x 4 = 140
and product of middle terms
= 70 x 2 = 140.
Sharing a ratio means something !
Consider the following example :
Raju purchased 3 pens for Rs. 15 and Anu purchased 10 pens for Rs. 50, whose pens are more expensive ?
Ratio of number of pens purchased by Raju to the number of pens purchased by Anu = 3 : 10.
Ratio of their costs = 15 : 50 = 3 : 10
Both the ratios 3 : 10 and 15 : 50 are equal.
Therefore, the pens were purchased for the same price by both.
![]()
TRY THIS (Page 339) :
Question 1.
Read the table and fill in the blanks:
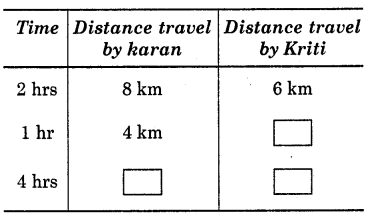
Solution:
(i) Distance travelled by Karan in 2 hrs = 8 km.
Distance travelled by Karan in 1 hr = \(\frac{8}{2}\) km = 4 km.
∴ Distance travelled
by Karan in 4 hrk = 4 x 4 = 16 km.
(ii) Distance travelled
by Kriti in 2 hrs = 6 km
Distance travelled
by Kriti in 1 hr = \(\frac{6}{2}\) km = 3 km
∴ Distance travelled
by Kriti in 4 hrs = 3 x 4 = 12 km.