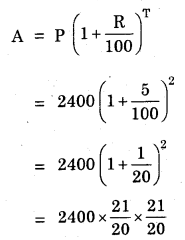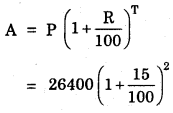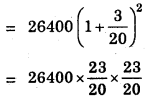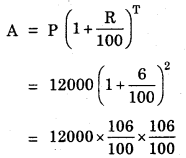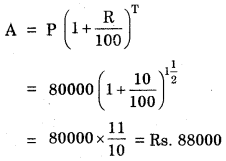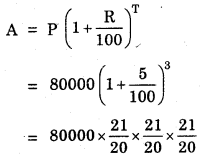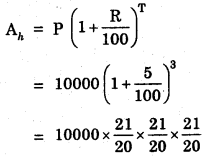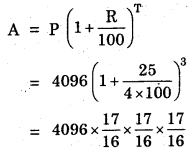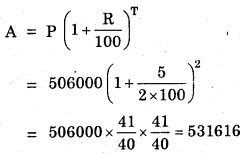Class 8

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.4

Question 1.
Multiply the binomials.
(i) (2x + 5) and (4x- 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l + 0.5 m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q²) and 3(pq – 2q²)
(vi)
Solution:
(i) (2x + 5) × (4x – 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15.

(ii) (y – 8) × (3y – 4) = 3y² – 4y – 24y + 32
= 3y² – 28y + 32.

(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= 6.25l² + 1.25lm – 1.25lm + 0.25m²
= 6.25l² + 0.25m².

(iv) (a + 3b) × (x,+ 5)
= ax + 5a + 3bx + 15b
= ax + 3bx + 5a + 15b.

(v) (2pq + 3q²) × (3pq – 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²a² + 5pq³ – 6q⁴.

(vi)

Question 2.
Find the product.
(i) (5 – 2x)(3 + x)
(ii) (x + 7y)(7x – y)
(iii) (a² + b) (a + b²)
(iv) (p² – q²) (2p + q).
Solution:
(i) (5 – 2x) × (3 + x)
= 15 + 5x – 6x – 2x²
= 15 – x – 2x².

(ii) (x + 7y) × (7x -y)
= 7x² – xy + 49xy – 7y²
= 7x² – 7y² + 48xy.

(iii) (a² + b) × (a + b²)
= a³ + a²b² + ab + b³
= a³ + b³ + a²b² + ab.

(iv) (p² – q²) × (2p + q)
= 2p³ + p²q – 2pq² – q³
= 2p³ – q³ + p²q – 2pq².

Question 3.
Simplify :
(i) (x² – 5) (x + 5) + 25
(ii) (a² + 5) (b³ + 3) + 5
(iii) (t + s²) (t² – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
(v) (x +y) (2x +y) + (x + 2y) (x – y)
(vi) (x + y) (x² – xy + y²)
(vii) (1.5x – 4y) (1.5x + 4y + 3)- 4.5x + 12y
(viii) (a + b + c) (a + b – c).
Solution:
(i) (x² – 5) × (x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x.

(ii) (a² + 5) × (b³ + 3) + 5
= a²b³ + 3a² + 5b² + 15 + 5
= a²b³ + 3a² + 5b³ + 20.

(iii) (t + s²) (t² – s)
= t³ – st + s²t² – s³
= t³ – s³ + s² + t² – st.

(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac +bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac.

(v) (x + y) × (2x + y) + (x + 2y) x (x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 3x² – y² + 4xy.

(vi) (x + y) × (x² – xy + y²)
= x³ – x²y + xy² + x²y – xy² + y³
= x³ + y³.

(vii) (1.5x – 4y) × (1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 60xy + 4.5x – 60xy – 16y² – 12y – 4.5x + 12y
= 2.25x².

(viii) (a + b + c) × (a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + b² – c² + 2ab.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.3

Question 1.
Carry out the multiplication of the expressions in each of the following pairs :
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a² – 9, 4a
(v) pq + qr + rp, 0.
Solution:
(i) 4p(q + r) = 4pq + 4pr.
(ii) ab × (a – b) = a²b – ab².
(iii) (a + b) × (7a²b²) = 7a²b² + 7a²b³.
(iv) (a² – 9) × 4a = 4a³ – 36a.
(v) (pq – qr + rp) × 0 = 0

Question 2.
Complete the table.

Solution:
(i) ab + ac, + ad
(ii) 5x²y + 5xy² – 25xy
(iii) 6p³ – 7p² + 5p
(iv) 4p⁴q² – 4p²q⁴
(v) a²bc + ab²c + abc².

Question 3.
Find the product.
(i) (a²) × (2a²²) × (4a²⁶)

(iv) x × x² × x³ × x⁴.
Solution:
(i) a² × 2 × a²² × 4 × a²⁶ = 8a⁵⁰.

(iv) x × x² × x³ × x⁴ = x¹⁰.

Question 4.
(a) Simplify 3x (4x – 5) + 3 and find its values for
(i) x = 3
(ii) x = \(\frac{1}{2}\)

(b) Simplify a (a² + a + 1) + 5 and find its value for
(i) a = 0
(ii) a = 1
(iii) a = -1.
Solution:
(a) 3x (4x – 5) + 3 = 12x² – 15x + 3
(i) If x = 3, 12 × (3)² – 15 × 3 + 3
= 12 × 9 – 45 + 3
= 108 – 42 = 66.

(ii) If x = \(\frac{1}{2}\) 12 × (\(\frac{1}{2}\))² – 15 × \(\frac{1}{2}\) + 3
= 12 × \(\frac{1}{4}\) – \(\frac{15}{2}\) + 3
= 6 – \(\frac{15}{2}\) = \(\frac{12-15}{2}\) = \(\frac{-3}{2}\)

(b) a(a² + a + 1) + 5 = a³ + a² + a + 5
(i) If a = 0
a³ + a² + a + 5 = 0³ + 0² + 0 + 5 = 5.

(ii) If a = 1,
a³ + a² + a + 5 = (1)³ + 1² + 1 + 5
= 1 + 1 + 1 + 5 = 8.

(iii) If a = 1
a³ + a² + a + 5 = (-1)³ + (-1)² + (-1) + 5
= 1 + 1 – 1 + 5 = 6.

Question 5.
(a) Add : p(p – q), q(q – r) and r(r – p)
(b) Add : 2x (z – x – y) and 2y (z – y- x)
(c) Subtract : 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c).
Solution:
(a) Add : (p² – pq) + (q² – qr) + (r² – rp)
= p² + q² + r² – pq – qr – rp.

(b) Add : (2xz – 2x² – 2xy) + (2yz – 2y² – 2xy)
= 2xz – 2x² – 2xy + 2yz – 2y² – 2xy
= -2x² – 2y² – 4xy + 2xz + 2yz.

(c) Subtract : (40ln – 12lm + 8l²) – (3l² – 12lm + 15ln)
= 40ln – 12lm + 8l² – 3l² + 12lm – 15ln
= 5l² + 25ln.

(d) Subtract : (-4ca + 4bc + 4c²) – (3a² + 3ab + 3ac – 2ab + 2b² – 2bc)
= (-4ca + 4bc + 4c²) – (3a² + 2b² + ab — 2bc + 3ac)
= -4ac + 45c + 4c² – 3a² – 2b² – ab + 25c – 3ac
= -3a² – 2b² + 4c² – ab + 6bc – 7ac.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Question 1.
Find the product of the following pairs of monomials :
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p³, -3p
(v) 4p, 0.
Solution:
(i) 4 × 7p = (4 × 7) × p
= 28p.

(ii) -4p × 7p = (-4 × 7) × (p × p)
= -28p².

(iii) -4p × 7pq = (-4 × 7) × (p × pq).
= -28p²q.

(iv) 4p3, -3p = [(4) × (-3)] × (p3 × p)
= -12 p⁴.

(v) 4p × 0 = (4 × 0) × p = 0 × p = 0.

Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Solution:
Area of rectangle = l × b sq. unit
(i) If l = p, b = q
Area of rectangle = p × q= pq sq.\unit.

(ii) If l = 10m, b = 5n
Area of rectangle = 10m × bn
= 50mn sq. unit.

(iii) If l = 20x², b =-5y²
Area of rectangle = 20x² × 5y²
= 100x²y² sq. unit

(iv) If l = 4x, b = 3x²
Area of rectangle = 4x × 3x² = 12x³sq. unit

(v) If l = 3mn, b = 4np
Area of rectangle = 3mn × 4np
= 12mn²p sq. unit.

Question 3.
Complete the table of products.

Solution:
Complete the table of products as shown in Table :

Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively:
(i) 5a, 3a², 7a⁴,
(ii) 2p, 4p, 8r,
(iii) xy, 2x²y, 2xy²,
(iv) a, 2b, 3c.
Solution:
Volume of cuboid = l × b × h

(i) l = 5a, b = 3a², h = 7a⁴
Volume of rectangular box
= l × b × h cubic unit
= 5a × 3a² × 7a⁴
= (5 × 3 × 7) × (a × a2 × a4)
= 105a⁷ cubic unit.

(ii) l = 2p, b = 4q, h = 8r
v = l × b × h, = 2p × 4q × 8r
= (2 × 4 × 8) × (p × q × r)
= 64pqr.

(iii) l = xy, b = 2x²y, h = 2xy²
v = xy × 2x²y × 2xy²
= (1 × 2 × 2) × (xy × x²y × xy²)
= 4x⁴y⁴.

(iv) l = a, b = 2b, h = 3c
v = l × b × h = a × 2b × 3c
= (1 × 2 × 3) (a × b × c) = 6abc.

Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a², a³
(iii) 2, 4y, 8y², 16y³
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp.
Solution:
(i) xy × yz × zx = x²y²z².
(ii) a × (-a²) × (a³) = -a⁶.

(iii) 2 × 4y × 8y² × 16y³
= (2 × 4 × 8 × 16) × (y × y² × y³)
= 1024 y⁶.

(iv) a × 2b × 3c × 6abc
= (2 × 3 × 6) x (a x b × c × abc)
= 36a²b²c².

(v) mx (-mn) × mnp = -m³n²p.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities Exercise 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i) 5xyz² – 3zy
(ii) 1 + x + x²
(iu) 4x²y² – 4x²y²z² + z²
(iv) 3 – pq + qr – rp
(v) \(\frac{x}{2}\) + \(\frac{y}{2}\) – xy
(v) 0.3a – 0.6ab + 0.5b.
Solution:
(i) There are two terms; 5xyz² and -3zy
Coefficient of 5xyz² = 5
Coefficient of-3zy = -3

(ii) There are three terms; 1, x and x²
Coefficient of x = 1
Coefficient of x² = 1

(iii) There are three terms; 4x²y², -4x²y²z², z².
Coefficient of 4x²y² = 4
Coefficient of -4x²y²z² = -4
Coefficient of z² = 1

(iv) There are four terms; 3, -pq, qr and – rp.
Coefficient of -pq = -1
Coefficient of qr = 1
Coefficient of -rp = -1.

(v) There are three terms; \(\frac{x}{2}\) , \(\frac{y}{2}\), -xy
Coefficient of \(\frac{x}{2}\) = \(\frac{1}{2}\)
Coefficient of \(\frac{y}{2}\) = \(\frac{1}{2}\)
Coefficient of-xy = -1

(vi) There are three terms; 0.3a, -0.6ab, 0.5b.
Coefficient of 0.3a = 0.3
Coefficient of-0.6a6 = -0.6 .
Coefficient of 0.56 = 0.5.

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories ?.
x + y, 1000, x + x² + x³ + x⁴, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y³, 5x – 4y + 3xy, 4z – 15z², ab + bc + cd + da, pqr, p²q + pq², 2p + 2q.
Solution:
Monomial = 1000, par
Binomial = x + y, 2y – 3y², 4z – 15z², p²q + pq², 2p + 2q
Trinomial = 7 + y + 5x, 2y – 3y² + 4y³, 5x – 4y + 3xy
Polynomial = x + x² + x³ + x⁴, ab + bc + cd + da,

Question 3.
Add the following :
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl.
Solution:
(i) Add :

Question 4.
(a) Subtract 4a – 7ab + 36 + 12 from 12a – 9ab + 5b – 3
(6) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + bp²q.
Solution:
(a)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 Comparing Quantities InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 8 Comparing Quantities InText Questions

Try These (Page 119)

Question 1.
In a primary school, the parents were asked about the number of hours they spend per day in helping their children to do homework. There were 90 parent who helped for \(\frac{1}{2}\) hour to 1\(\frac{1}{2}\) hours. The distribution of parents according to time for which, they said they helped is given in the adjoining figure; 20% helped for more than 1\(\frac{1}{2}\) hours per day; 30% helped for \(\frac{1}{2}\) hour to 1\(\frac{1}{2}\) hours; 50% did not help at all. It

Using this answer the following :
(i) How many parents were surveyed ?
(ii) How many said that they did not help ?
(iii) How many said that they helped for more than 1\(\frac{1}{2}\) hours ?
Solution:
(i) Let total no. of parents be x 30% of x helped for \(\frac{1}{2}\) hour to 1\(\frac{1}{2}\) hour
So 30% of x = 90
\(\frac{30}{100}\) × x = 90 or x = \(\frac{90 \times 100}{30}\) = 300
Number of parents = 300.

(ii) 50% parents did not help,
So number of parents did not help
= 50% of 300 = \(\frac{50}{100}\) × 300 = 150

(iii) 20% parents helped for more than 1\(\frac{1}{2}\) hours
So, number of such parents
= 20% of 300 = \(\frac{20}{100}\) × 300 = 60

Try These (Page 121)

Question 1.
A shop gives 20% discount. What would the sale price of each of these be ?
(a) A dress marked at Rs. 120.
(b) A pair of shoes marked at Rs. 750.
(c) A bag marked at Rs. 250.
Solution:
(a) 20% discount means On Rs. 100, discount is Rs. 20
On Re. 1 = Rs. \(\frac{20}{100}\)
∴ On 120 = \(\frac{20}{100}\) × 120 = 24
Sale price = M.P. – Discount
= 120 – 24 = 96
∴ Sale price = Rs. 96

(b) 20% discount means
20% discount on M.P.
⇒ Selling price = 100 – 20
= 80% on M.P.
∴ Sale price of shoe of MP Rs. 750
= 80% of 750
= \(\frac{80}{100}\) × 750 = 600
∴ Sale price of shoe = Rs. 600.

(c) 20% discount means
Selling price = 80% of M.P.
∴ Selling price of bag of M.P. Rs. 250
= 80% of 250
= \(\frac{80}{100}\) × 250 = 200
∴ Sale price of bag = Rs. 200.

Question 2.
A table marked at Rs. 15,000 is available for Rs. 14,400. Find the discount given and the discount per cent.
Solution:
M.P. = Rs. 15000
S.P. = 1440
Discount = ?
Discount % = ?
Discount = M.P. – S.P.
= 15000 – 14400 = 600
Discount % = \(\frac{Discount}{M.P.}\) × 100
= \(\frac{600}{15000}\) × 100 = 4%
Discount – Rs. 600, discount % = 4.

Question 3.
An almirah is sold at Rs. 5,225 after allowing a discount of 5%. Find its marked price.
Solution:
M.P. = ?
S.P. = Rs. 5,225
Discount % = 5 %

Try These (Page 123)

Question 1.
Find selling price (S.P.) if a profit of 5% is made on
(a) a cycle of Rs. 700 with Rs. 50 as overhead charges.
(b) a lawn mower bought at Rs. 1150 with Rs. 50 as transportation charges.
(c) a fan bought for Rs. 560 and expenses of Rs. 40 made on its repairs.
Solution:
(a) Cycle of worth Rs. 700
Overhead charges on cycle = 50
∴ C.P. of cycle = 700 + 50 = 750
Profit % = 5
∴ Profit of Rs. 5 on C.P. of Rs. 100
⇒ S.P. = (100 + 5)% of C.P.
∴ S.P. of cycle of C.P. Rs. 750 = 105% of 750
= \(\frac{105}{100}\) × 750 = 787.50
∴ S.P. of cycle = Rs. 787.50.

(b) Lawn mower bought in Rs. 1150
Transportation charge = Rs. 50
∴ C.P. of lawn mower = 1150 + 50 = 1200
5% profit on lawn mower is made
∴ S.P. = 105% of C.P.
= \(\frac{105}{100}\) × 1200 = 1260
∴ Sale price of lawn mower = Rs. 1260.

(c) Fan bought in Rs. 560
Expenses on its repairs = Rs. 40
∴ C.P. of fan = 560 + 40 = 600
5% profit on fan is made
∴ S.P. of fan = 105% of C.P. of fan
= \(\frac{105}{100}\) × 600 = 630
S.P. of fan = Rs. 630.

Question 2.
A shopkeeper bought two T.V. sets at Rs. 10,000 each. He sold one at a profit of 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.
Solution:
Overall C.P. of each T.V. set = Rs. 10,000
One is sold at a profit of 10%
⇒ If C.P. is Rs. 100, S.P. is Rs. 110
Therefore, when C.P. is Rs. 10,000,
Then, S.P. = Rs. \(\frac{110}{100}\) × 10000 = 11000
In second case, T.V. at a loss of 10%
⇒ If C.P. is Rs. 100, S.P. is Rs. 90
Therefore, when C.P. is Rs. 10,000
Then, S.P. = Rs. \(\frac{90}{100}\) × 10000 = 9000
Total C.P. of two sets of T.V.
= Rs. 10000 + Rs. 10000
= Rs. 20,000
Total S.P. of two sets of T.V.
= Rs. 11000 + Rs. 9000
= Rs. 20,000
Since Total S.P. = Total C,P.
⇒ Neither profit nor loss.

Try These (Page 124-125)

Question 1.
Find the buying price of each of the following when 5% S.T. is added on the purchase of
(a) A towel at Rs. 50.
(b) Two bars of soap at Rs. 35 each.
(c) 5 kg of flour at Rs. 15 per kg.
Solution:
(a) S.T. of Rs 50 = 50 × \(\frac{10}{100}\) = Rs. 5
Bill amount = Cost of towel + sales tax
= 50 + 5 = Rs. 55.

(b) S.T. of Rs. 35 = 35 × \(\frac{10}{100}\) = Rs. 3.50
∴ Bill amount = cost of two bars of soap + S.T.
= 70 + 7 = Rs. 77.

(c) Cost of 5 kg flour = 5 × 15 = Rs. 75
Sales tax = Rs. 75 × \(\frac{10}{100}\)
= Rs. 7.5
Bill amount = Cost of flour + S.T.
= 75 + 7.5
= Rs. 82.50.

Question 2.
If 8% VAT is included in the prices, find the original price of
(a) A TV bought for Rs. 13,500.
(b) A shampoo bottle bought for Rs. 180.
Solution:
(a) 8% VAT mean an article of Rs. 100
will costs Rs. 100 + 8 = Rs. 108
Therefore, when price including VAT is Rs. 108, original price = Rs. 100
∴ When price including VAT is Rs. 13500
Original price = \(\frac{100}{108}\) × 13500 = 12500
∴ Original price of T.V. = Rs. 12500.

(b) 8% VAT included in the price
⇒ When price including VAT is Rs. 108, original price = Rs. 100
∴ When price including VAT is Rs. 180, original price
= \(\frac{100}{108}\) × 180 = 166.67
∴ Original price of shampoo = Rs. 166.67.

Try These (Page 126)

Question 1.
Find interest and amount to be paid on Rs. 15000 at 5% per annum after 2 years.
Solution:
P = Rs. 15000, R = 5% per annum, T = 2 year, I = ?, A = ?
I = \(\frac{P \times R \times T}{100}\) × \(\frac{5}{100}\) × 2 = Rs. 1500
A = P + I
= Rs. 15000 + Rs. 1500
= Rs. 16500.

Try These (Page 129)

Question 1.
Find C.I. on a sum of Rs. 8000 for 2 years at 5% per annum compounded annually.
Solution:
P = Rs. 8000, R = 5% per annum, T = 2 year, C.I. = ?

= 20 × 21 × 21 = Rs. 8820
C.I. = A – P
= Rs. 8820 – Rs. 8000
= Rs. 820.

Try These (Page 130)

Question 1.
Find the time period and rate for each.
1. A sum taken for 1\(\frac{1}{2}\) years at 8% per annum is compounded half yearly.
2. A sum taken for 2 years at 4% per annum compounded half yearly.
Solution:
1. If the time period yearly and the interest is compounded half yearly, then the time, T will be T × 2
∴ T = 1\(\frac{1}{2}\) year
= \(\frac{3}{2}\) × 2 = 3 years.
and, if the rate of interest is R% per annum and the interest is compounded half yearly, then the rate of interest will be \(\frac{R}{2}\) % per half hear.
R = 8% = \(\frac{R}{2}\)
= 4% per half year.

2. If the time period yearly and the interest is compounded half yearly then the time, T will be T × 2
∴ T = 2 years = 2 × 2 = 4 years
and, if the rate of interest is R% per annum and the interest is compounded half yearly, then the rate of interest will be \(\frac{R}{2}\) % per half year.
∴ R = 4% = \(\frac{4}{2}\)%
= 2% per half year.

Try These (Page 131)

Question 1.
Find the amount to be paid
(i) At the end of 2 years on Rs. 2,400 at ty5% per annum compounded annually.
(ii) At the end of 1 year on Rs. 1,800 at 8% per annum compounded quarterly.
Solution:
(i) A = ?, T = 2 years, P = Rs. 2400, R = 5% per annum compounded annually.

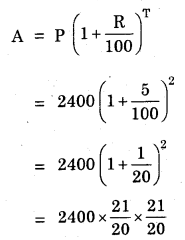
= 6 × 441 = Rs. 2646
∴ Amount = Rs. 2646.

(ii) R = 8% per annum compounded quarterly = 2% per quarterly
T = 1 year = 4 quarter
P = Rs. 1800, A = ?

= 1800 × \(\frac{51}{50}\) × \(\frac{51}{50}\)
= Rs. 1872.7
Amount = Rs. 1872.72.

Try These (Page 133)

Question 1.
A machinery worth Rs. 10,500 depreciated by 5%. Find its value after one year.
Solution:
P = Rs. 10500, R = 5%, T = 1 year
Cost of machinery after one year
= P(1 – \(\frac{R}{100}\))¹ = 10500(1 – \(\frac{5}{100}\))¹
= 10500(1 – \(\frac{1}{20}\))¹
= 10500 \(\frac{19}{20}\)
= 525 × 19 = Rs. 9975.

Question 2.
Find the population of a city after 2 years, which is at present 12 lakh, if the rate of increase is 4%.
Solution:
T = 2 year, present population, P = 12 lakh
R = 4%, A = ?
= 1200000 (1 + \(\frac{4}{100}\))²
= 1200000(1 + \(\frac{1}{25}\))²
= 1200000 × \(\frac{26}{25}\) × \(\frac{26}{25}\)
= 1297920
∴ Population after 2 years
= 1297920.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 Comparing Quantities Ex 8.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 8 Comparing Quantities Exercise 8.3

Question 1.
Calculate the amount and compound interest on :
(a) Rs. 10,800 for 3 years at 12\(\frac{1}{2}\)% per annum compounded annually.
(b) Rs. 18,000 for 2\(\frac{1}{2}\) years at 10% per annum compounded annually.
(c) Rs. 62,500 for 1\(\frac{1}{2}\) years at 8% per annum compounded half yearly.
(d) Rs. 8,000 for 1 year at 9% per annum compounded half yearly. (You could use the year by year calculation using S.I. formula to verify).
(e) Rs. 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) A = ?, C.I. = ?, P = Rs. 10,800,
T = 3 years, R = 12 \(\frac{1}{2}\)% per annum
A = P(1 + \(\frac{R}{100}\))^T
= 1080o(1 + \(\frac{25}{2}\) × \(\frac{1}{100}\))³
= 10800(\(\frac{17}{16}\))³
= 10800 × \(\frac{17}{16}\) × \(\frac{17}{16}\) × \(\frac{17}{16}\)
= Rs. 12954.20
C.I. = A – P
= Rs. 1295.4.20 – Rs. 10800
= Rs. 2154.20.

(b) P = Rs. 18000, T = 2\(\frac{1}{2}\) years, R = 10% per annum compounded annually, A = ?, C.I. = ?
A = P(1 + \(\frac{R}{100}\))^T
= 18000(1 + \(\frac{10}{100}\))^{2\(\frac{1}{2}\)}
So amount for 2 years is given by
A = Rs. 18000(1 + \(\frac{10}{100}\))²
= 18000(1 + \(\frac{1}{10}\))²
= 18000 × \(\frac{11}{10}\) × \(\frac{11}{10}\)
= 180 × 121 = Rs. 21780
Rs. 21780 would act as principal for next \(\frac{1}{2}\) year. We find S.I. on Rs. 21780 for \(\frac{1}{2}\) year
S.I = Rs. \(\frac{21780 \times \frac{1}{2} \times 10}{100}\)
= Rs. 1089
Interest for two years
= Rs. 21780 – Rs. 18000
= Rs. 3780
Interest for next \(\frac{1}{2}\) year = Rs. 1089
Therefore, total compound interest
= Rs. 3780 + Rs. 1089
= Rs. 4869
A = P + C.I.
= Rs. 18000 + Rs. 4869
= Rs. 22869.

(c) P = Rs. 62500, T = 1\(\frac{1}{2}\) years = 3 half years, R = 8% per annum = 4% per half yearly, A = ?, C.I. = ?

= Rs 70304
C.I. = A – P
= Rs. 70304 – Rs. 62500
= Rs. 7804.

(d) P = Rs. 8000, T = 1 year = 2 half years, R = 9% per annum = \(\frac{9}{2}\) % per half year, A = ?, C.I. = ?

= Rs. 8736.20
C.I. = A – P
= Rs. 8736.20 – Rs. 8000
= Rs. 736.20.

(e) P = Rs. 10000, T = 1 year = 2 half years, R = 8% per annum = 4% per half year, A = ?, C.I. = ?

= Rs. 10816
C.I. = A – P
= Rs. 10816 – Rs. 10000
= Rs. 816.

Question 2.
Kamla borrowed Rs. 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan ?
[Hint : Find A for 2 years with interest is compounded yearly and then find S.I. on the 2nd year amount for 4/12 years]
Solution:
P = Rs. 26400, R = 15% per annum, T = 2 years and 4 months, A = ?


= 66 × 23 × 23
= Rs. 34914
Rs. 34914 would act as principal for next 4 months i.e. \(\frac{1}{3}\) year
So S.I. = P × R × T
= 34914 × \(\frac{15}{100}\) × \(\frac{1}{3}\)
= Rs. 1745.70
Amount paid by Kamla after 2 years
= Rs. 34914 + Rs. 1745.70
= Rs. 36659.70.

Question 3.
Fabina borrows Rs. 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much ?
Solution:
In case of Fabina :
P = Rs. 12500,
R = 12% per annum, T = 3 years
S.I = P × R × T
= 12500 × \(\frac{12}{100}\) × 3 = RS. 4500.
In case of Radha :
P = Rs. 12500,
R = 10% per annum,
T = 3 years, C.I. = ?

= Rs. 16637.50
C.I. = A – P
= Rs. 16637.50 – Rs. 12500
= Rs. 4137.50
It is obvious that Fabina would pay more interest by Rs. 4500 – Rs. 4137.50 = Rs. 362.50 So,
Fabina paid Rs. 362.50 more than Radha.

Question 4.
I borrowed Rs. 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay ?
Solution:
P = Rs. 12000, R = 6% per annum, T = 2 years, S.I. = ?, C.I. = ?
In case of simple interest:
S.I = P × R × T
= 12000 × \(\frac{6}{100}\) × 2
= Rs. 1440
In case of compound interest:

= Rs. 13483.20
So, Amount = Rs. 13483.20
∴ C.I. = A – P
= Rs. 13483.20 – Rs. 12000
= Rs. 1483.20
It is obvious that C.I. > S.I
So extra amount paid in case of C.I. is
= Rs. 1483.20 – Rs. 1440
= Rs. 43.20.

Question 5.
Vasudevan invested Rs. 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months ?
(ii) after 1 year ?
Solution:
P = Rs. 60000,
R = 12% per annum compounded half yearly
= 6% half yearly
A₆ = ?
A₁₂ = ?
T₆ = 6 months = 1 half year
T₁₂ = 1 year = 2 half years

(i) Amount after 6 months

= Rs. 67416.
∴ A₁₂ = Rs. 67416.

Question 6.
Arif took a loan of Rs. 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he
would be paying after 1\(\frac{1}{2}\) years if the interest is
(i) Compounded annually.
(ii) Compounded half yearly.
Solution:
P = Rs. 80000,
R = 10% per annum,
T = 1\(\frac{1}{2}\) years
= 5% half yearly = 3 half years
In 1st Case : When amount calculated annual compounding

Rs. 88000 would be principal for half year to calculate S.I. for \(\frac{1}{2}\) year
S.I. = P × R × T
= 88000 × \(\frac{10}{100}\) × \(\frac{1}{2}\)
= Rs. 4400
∴ C.I. for 1\(\frac{1}{2}\) on given principal
= (Rs. 88000 – Rs. 80000) + Rs. 4400
= Rs. 12400
So, A = P + C.I.
= Rs. 80000 + Rs. 12400
= Rs. 92400
In 2nd Case : When amount calculated half yearly compounding

= Rs. 92610
Difference in amount in both the cases
= Rs. 92610 – Rs. 92400
= Rs. 210.

Question 7.
Maria invested Rs. 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the 3rd year.
Solution:
(i) P = Rs. 8000, R = 5% per annum, T = 2 year, T = 3 year, A₂ = ?, A₃ = ?
Amount after 2 years,

Amount credited after 2 years = Rs. 8820.
Amount after 3 years,

= Rs. 9261
∴ Interest for 3rd year = A₃ – A₂
= Rs. 9261 – Rs. 8820
= Rs. 441.

Question 8.
Find the amount and the compound interest on Rs. 10,000 for 1\(\frac{1}{2}\) years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually ?
Solution:
P = Rs. 10000
T = 1\(\frac{1}{2}\) years = 3 half years
R = 10% per annum = 5% half yearly
A_h =?, A_a = ?

= Rs. 11576.25
So, Amount = Rs. 11576.25
∴ C.I. = A – P
= Rs. 11576.25 – Rs. 10000
= Rs. 1576.25
If n = 1\(\frac{1}{2}\) = \(\frac{3}{2}\) years
A_a = P(1 + \(\frac{R}{100}\))^T

= 1000 × 1.05 = Rs. 11550
∴ C.I. = A_a – P = 11550 – 10000
= Rs. 1550.
or, Rs. 11000 would be principal for \(\frac{1}{2}\) year to calculate S.I. for \(\frac{1}{2}\) year.
S.I. = P × R × T
= 11000 × \(\frac{10}{100}\) × \(\frac{1}{2}\) = Rs. 550
∴ C.I. = (Rs. 11000 – Rs. 10000) + Rs. 550 = Rs. 1550
It is obvious that C.I. calculated half yearly is greater than that when calculated yearly.
Extra amount of interest = Rs. 1576.25 – Rs. 1500 = Rs. 76.25.

Question 9.
Find the amount which Ram will get on Rs. 4096, if have gave it for 18 months at 12\(\frac{1}{2}\) % per annum, interest being compounded half yearly.
Solution:
P = Rs. 4096,
T = 18 months = 3 half years,
R = 12\(\frac{1}{2}\) % per annum
= \(\frac{25}{4}\) % per half year
A = ?

= Rs. 4913

Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum
(i) find the population in 2001.
(ii) what would be its population in 2005 ?
Solution:
(i) P = 54000, R = 5% per annum, A = ?, T = 2 years
Population before 2 years

(ii) For population in 2005 i.e. 2 years after 2003
P = 54000, T = 2 years, R = 5% per annum, A = ?

∴ Population in 2005 be 59535.

Question 11.
In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Initial count of bacteria P = 506000, T = 2 hour
Rate of increasing bacteria R = 2.5% per hour, A = ?

∴ Count of bacteria after 2 hour = 531616.

Question 12.
A scooter was bought at Rs. 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
P = Rs. 42000, R = 8% per annum, T = 1 year, A = ?

Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 Comparing Quantities Ex 8.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 8 Comparing Quantities Exercise 8.2

Question 1.
A man got a 10% increase in his salary. If his new salary is Rs. 1,54,000, find his original salary.
Solution:
10% increase in salary means
If previous salary is Rs. 100, increased salary = Rs. 110
If new salary is Rs. 110, original salary is Rs. 100
New salary is Rs. 1,54,000, original salary is = \(\frac{100}{110}\) × 154000 = 1,40,000
Original salary = Rs. 1,40,000.

Question 2.
On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the Zoo on Monday.
Solution:
On Sunday Zoo visitor = 845 persons
On Monday Zoo visitor = 169 persons
Decrease in people visiting Zoo on Monday
= 845 – 169 = 676
Percent decrease on Monday
= \(\frac{Decrease}{Visitor on Sunday}\) × 100
= \(\frac{676}{845}\) × 100 = 80%

Question 3.
A shopkeeper buys 80 articles for Rs. 2,400 and sells them for a profit of 16%. Find the selling price of one article.
Solution:
C.P. of all 80 articles = Rs. 2400
16% profit means if C.P. is Rs. 100, S.P. is Rs. 116
Therefore, if C.P. is Rs. 2400,
S P = \(\frac{116}{100}\) × 2400 = 2784
S.P. of 80 articles = Rs. 2784
∴ S.P. of one article = Rs. 34.80.

Question 4.
The cost of an article was Rs. 15,500. Rs. 450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Solution:
C.P. of article = Rs. 15500
Charge on its repairing = Rs. 450
So, new C.P. = Rs. 15500 + Rs. 450
= 15950
At profit of 15% is sold
So, S.P. = 115% of C.P,
= \(\frac{115}{100}\) × 15950
= 18342.50
∴ S.P. = Rs. 18342.50.

Question 5.
A VCR and TV were bought for Rs. 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss percent on the whole transaction.
Solution:
C.P. ofT.V. = Rs. 8000
C.P. of VCR = Rs. 8000
4% loss on VCR means
If C.P. is Rs. 100, S.P. is Rs. 96
So, if C.P. is 8000, S.P. will be
= \(\frac{96}{100}\) × 8000 = 7680
∴ S.P. of VCR = Rs. 7680
8% profit on TV means
If C.P. is Rs. 100, S.P. is Rs. 108
So if C.P. is Rs. 8000, S.P. will be
\(\frac{108}{100}\) × 8000 = 8640
∴ S.P. of T.V. = Rs. 8640
Overall C.P. of TV and VCR
= 8000 + 8000 = 16,000
Overall S.P. of TV and VCR
= 7680 + 8640 = 16320
∵ Overall S.P. > Overall C.P.
⇒ Profit of Rs. (16320 – 16000)
= Rs. 320.

Question 6.
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs. 1450 and two shirts marked at Rs. 850 each ?
Solution:
10% discount on marked price (M.P.)
⇒ Article of M.P. Rs. 100, has S.P. = Rs. 90
So, if article of M.P. Rs. 1450 has S.P.
= Rs.\(\frac{90}{100}\) × 1450
= Rs. 1305
and if the article of M.P. 1700 has S.P.
= Rs. \(\frac{90}{100}\) × 1700 = Rs. 1530
Two shirts M.P. = 850 × 2 = Rs. 1700
So customer have to pay for Jeans and two shirts
= Rs. 1305 + Rs. 1530 = Rs. 2835.

Question 7.
A milkman sold two of his buffaloes for Rs. 20,000 each. On one he made a gain of 5% and on the other a loss of 10%. Find his overall gain or loss.
[Hint: Find C.P. of each]
Solution:
S.P. of each buffalo = Rs. 20000
5% gain means
⇒ a profit of Rs. 5 on C.P. of Rs. 100
⇒ If S.P. is of Rs. 105, C.P. is Rs. 100
∴ If S.P. is Rs. 20,000
C.P. = Rs. \(\frac{100}{105}\) × 20,000 = 19048
∴ C.P. of one of buffalo = Rs. 19048
10% loss on other buffalo means
If S.P. is 90, C.P. is Rs.. 100
So, if S.P. is Rs. 20,000,
C.P. = Rs. \(\frac{100}{90}\) × 20,000
= Rs. 22222
∴ C.P. of other buffalo = Rs. 22222
∴ Overall S.P. = Rs. 20,000 + Rs. 20000
= Rs. 40,000
Overall C.P. = Rs. 19048 + Rs. 22222
= Rs. 41270
∵ Overall S.P. > Overall C.P.
⇒ Profit of Rs. (41270 – 40000) = Rs. 1270
∴ Net profit = Rs. 1270.

Question 8.
The price of a TV is Rs. 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Solution:
Price of TV = Rs. 13,000
Sale tax charge = 12%
∴ Sale tax on T.V.= 12% of Rs. 13,000
= Rs. \(\frac{12}{100}\) × 13000
= Rs. 1560
∴ Amound paid by Vinod for TV
= Rs. 13000 + Rs. 1560
= Rs. 14560.

Question 9.
Arun bought a pair of skates of a sale where the discount given was 20%. If the amount he pays is Rs. 1,600, find the marked price.
Solution:
20% discount means
For M.P. of Rs. 100, S.P.
= Rs. (100 – 20) = Rs. 80
So, if S.P. = Rs. 80, M.P. is Rs. 100
If S.P. = Rs. 1600, M.P. will be Rs. \(\frac{100}{80}\) × 1600
= 2000.
M.P. of skates Rs. 2000.

Question 10.
I purchased a hair-dryer for Rs. 5,400 including 8% VAT. Find the price before VAT was added.
Solution:
8% VAT included means.
Rs. 8 is added to original price of Rs. 100
⇒ If including VAT price is Rs. 108, original price = Rs. 100
So including VAT price is Rs. 5400, original price
= RS \(\frac{100}{108}\) × 5400
= Rs. 5000
∴ Price before VAT = Rs. 5000.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 Comparing Quantities Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 8 Comparing Quantities Exercise 8.1

Question 1.
Find the ratio of the following :
(a) Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
(b) 5 m to 10 km.
(c) 50 paise to Rs. 5.
Solution:
(a) Ratio of speed of cycle to speed of scooter = 15 : 30 = 1 : 2

(b) Ratio of 5 m to 10 km
⇒ Ratio of 5 m to 100000 m = 5 : 100000 = 1 : 20000

(c) Ratio of 50 paise to Rs. 5
⇒ Ratio of 50 paise to 500 paise
= 50 : 500 = 1 : 10.

Question 2.
Convert the following ratios to percentages.
(а) 3 : 4
(b) 2 : 3
Solution:
(a) Ratio = 3 : 4
Fraction = \(\frac{3}{4}\)
Percentage = \(\frac{3 \times 25}{4 \times 25}\) = \(\frac{75}{100}\) = 75%

(b) Ratio = 2 : 3
Fraction = \(\frac{2}{3}\)
Percentage = \(\frac{2}{3} \times \frac{100}{100}\) = \(\frac{200}{3} \times \frac{1}{100}\)
= 66\(\frac{2}{3}\)%.

Question 3.
72% of 25 students are good in mathematics. How many are not good in mathematics ?
Solution:
Total percent good in mathematics and not good in mathematics = 100
72 + percentage of student not good in mathematics = 100
∴ Percentage of students not good in mathematics = 100 – 72 = 28
So number of students hot good in mathematics = 28% of 25
= \(\frac{28}{100}\) × 25 = 7 students.

Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all ?
Solution:
Let the total number of matches played by football team be x their win was 40%.
So, 40% of x = 10
\(\frac{40}{100}\) × x = 10
x = \(\frac{10 \times 100}{40}\) = 25
Number of played matches = 25.

Question 5.
If Chameli had Rs. 600 left after spending 75% of her money, how much did she have in the beginning ?
Solution:
Let she had Rs. x in the beginning
Chameli spent 75% of her money.
So she left 100 – 75 = 25% of her moriey.
So, 25% of x = Rs. 600
\(\frac{25}{100}\) × x = 600
x = \(\frac{600 \times 100}{25}\) = 2400
Chameli had Rs. 2400 in the beginning.

Question 6.
If 60% people in a city like cricket, 30% like football and the remaining like other games, then what percent of the people like other games ? If the total number of people are .50 lakh, find the exact number who like each type of game.
Solution:
Total percent = 100
60% people like cricket
30% people like football
remaining like other game
So 100 – (60 + 30) = 10% like other game.
Total no. of people = 50 lakh
No. of people like cricket
= 60% of 50 lakh
= \(\frac{60}{100}\) × 50 lakh = 30 lakh
No. of people like football
= 30% of 50 lakh on
= \(\frac{30}{100}\) × 50 lakh = 15 lakh
No. of people like other game
= 10% of 50 .lakh
= \(\frac{10}{100}\) × 50 lakh = 5 lakh.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 7 Cube and Cube Roots Exercise 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method s
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125.
Solution:
(i) 64 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)

= 2³ × 2³
= 2 × 2
∴ \(\sqrt[3]{64}\) = 4

(ii) 512 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)

= 2³ × 2³ × 2³
= 2 × 2 × 2
∴ \(\sqrt[3]{512}\) = 8

(iii) 10648 = \(\underline{2 \times 2 \times 2}\) × \(\underline{11 \times 11 \times 11}\)

= 2³ × 11³
= 2 × 11
∴ \(\sqrt[3]{10648}\) = 22

(iv) 27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5

= 2³ × 3³ × 5³
∴ \(\sqrt[3]{27000}\) = 2 × 3 × 5
= 30

(v) 15625 = 5 × 5 × 5 × 5 × 5 × 5

= 5³ × 5³
= 5 × 5
∴ \(\sqrt[3]{15625}\) = 25

(vi) 13824 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) ×  \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)

= 2³ × 2³ × 2³ × 3³
= 2 × 2 × 2 × 3
∴ \(\sqrt[3]{13824}\) = 24

(vii) 110592 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) ×  \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)

= 2³ × 2³ × 2³ × 2³ × 3³
= 2 × 2 × 2 × 2 × 3
∴ \(\sqrt[3]{110592}\) = 48

(viii) 46656 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)

= 2³ × 2³ × 3³ × 3³
= 2 × 2 × 3 × 3
∴ \(\sqrt[3]{46656}\) = 36

(ix) 175616 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{7 \times 7 \times 7}\)

= 2³ × 2³ × 2³ × 7³
= 2 × 2 × 2 × 7
∴ \(\sqrt[3]{175616}\) = 56

(x) 91125 = \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\)

= 3³ × 3³ × 5³
= 3 × 3 × 5
∴ \(\sqrt[3]{91125}\) = 45

Question 2.
State true or false.
(i) Cube of any odd number is even
(ii) A perfect cube does not end with two zeros
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution:
(i) False,
(ii) True,
(iii) True,
(iv) False,
(v) False,
(vi) False,
(vii) True

Question 3.
You ar told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution:
The given number is 1331
Step 1. From groups of three starting from the rightmost digit of 1331 is 1331.In this case one group 331 has three digits whereas 1 has only two digits.

Step 2. Take 331.
The digit 1 is at its one’s place.
We take the one’s place of the required cube root as 1.

Step 3. Take the other group is 1.
Cube of 1 is 1 and cube of 2 is 8.1 lies between 0 and 8.
The smaller number among 1 and 2 is 1. The one’s place of 1 is 1 itself. Take 1 as ten’s place of the cube root of 1331.
Thus, \(\sqrt[3]{1331}\) = 11

Similarly, 4913
Step 1. 4913
Step 2. Take 913
The digit 3 is at its one’s place we take the one’s place of the required cube root as (3 × 3 × 3 = 27)7.

Step 3. Take the other group is 4. Cube of 1 is 1 and cube of 2 is 8. 4 lies between 1 and 8.
The smaller number among 1 and 2 is 1. The one’s place of 1 is 1 itself. Take 1 as ten’s place of the cube root of 4913.
Thus, \(\sqrt[3]{4913}\) = 17

Similarly, 12167
Step 1. 12167
Step 2. 7 × 7 × 7 = 343 i.e. one’s place is 3
Step 3. 12, 2 × 2 × 2 = 8 and 3 × 3 × 3 = 27 8 < 12 < 27
The smaller number among 2 and 3 is 2. The one’s place of 2 is 2 itself. Take 2 as tens place of the cube root of 12167.
Thus, \(\sqrt[3]{12167}\) = 23

Similarly, 32768
Step 1. 32768
Step 2. 8 × 8 × 8 = 512
i.e. one’s place is 2
Step 3. 32, 3 × 3 × 3 = 27
4 × 4 × 4 = 64
The smaller number along 3 and 4 is 3. The one’s place of 3 is 3 itself. Take 3 as ten’s place of the cube root 32768.
Thus \(\sqrt[3]{32768}\) = 32

Haryana State Board HBSE 8th Class Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 7 Cube and Cube Roots Exercise 7.1

Question 1.
Which of the following numbers are not perfect cubes:
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656.
Solution:
(i) 216 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)

= 2³ × 3²
= (2 × 3)³
= (6)³
Which is a perfect cube.

(ii) 128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2

= 2³ × 2³ × 2
∴ 2 does not appear in a group of three.
Hence, 128 is not a percent cube.

(iii) 1000 = 2 × 2 × 2 × 5 × 5 × 5

= 2 × 5
= 10
Which is a perfect cube.

(iv) 100 = 2 × 2 × 5 × 5

Prime factor of 100 is
2 × 2 × 5 × 5
So, 100 is not a perfect cube.

(v) 46656 = 2 × 2 × 2 × 2 × 2 × 2 × 9 × 9 × 9

= 2 × 2 × 9
= 36
Which is a perfect cube.

Question 2.
Find the smallest number by which each of the following number must be multified to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100.
Solution:
(i) 243 = 3 × 3 × 3 × 3 × 3
The prime factor 3 × 3 = 9 does not appear in a group of three. Therefore 243 is not a perfect cube. To make it a cube, we need one more 3.
In that case,
243 × 3 = \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)
= 729,
which is a perfect cube.
Hence the required smallest number by which 243 should be multiplied to make a perfect is 3.

(ii) 256 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2 × 2
The prime factor 2 × 2 = 4 does not appear in a group of three. Therefore 256 is not a perfect cube. To make it cube, we need one more 2., In that case,
256 × 2 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
= 512
Hence the required smallest number by which 256 should be multiplied to make a perfect cube is 2.

(iii) 72 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3}\)
The prime factor 3 does not appear in a group of three. Therefore 72 is not a perfect cube. To make it a cube, we need one more 3. In that case
72 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)
or, 72 × 3
= 216,
which is a perfect cube.
Hence, the required smallest number by which 72 should be multiplied to make a perfect cube is 3.

(iv) 675 = \(\underline{3 \times 3 \times 3}\) × 5 × 5
The prime factor 5 does not appear in a group of three. Therefore 675 is not a perfect cube. To make it a cube, we need one more 5. In that case
675 × 5 = \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\)
= 3375.
which is a perfect cube.
Hence, the required smallest number by which 675 should be multiplied to make a perfect cube is 5.

(v) 100 = \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\)
The prime factor 2 and 5 do not appear in a group of three. Therefore 100 is not a perfect cube. To make it a cube, we need one more 2 and 5 respectively. In that case
100 × 10 = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
= 1000,
which is a perfect cube. Hence the required smallest number by which 100 should be multiplied to make a perfect cube is (2 × 5) = 10.

Question 3.
Find the smallest whole number by which each of the following numbers must be divided to obtain a perfect cube :
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704
Solution:
(i) 81 = \(\underline{3 \times 3 \times 3}\) × 3
The prime factor 3 does not appear in a group of three. So 81 is not a perfect cube. In the factorisation 3 appears only one time. So if we divide 81 by 3, then the prime factorisation of the quotient will not contain 3.
81 ÷ 3 = 3 × 3 × 3
Further the perfect cube in that case is 81 , 3 = 27. Hence the smallest whole number by which 81 should be divided to make it perfect cube is 3.

(ii) 128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2
The prime factor 2 does not appear in a group of three. So 128 is not a perfect cube. In the factorisation 2 appear only one time. So if we divide 128 by 2, then the prime factorisation of the quotient will not contain 2
128 ÷ 2 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
Further the perfect cube in that case is
128 ÷ 2 = 64.
Hence the smallest whole number by which 128 should be divided to make it perfect cube is 2.

(iii) 135 = \(\underline{3 \times 3 \times 3}\) × 5
The prime Factor 5 × 5 = 25 does not appear in a group of three. So, 135 is not a Perfect Cube. In the factorisation 5 appears only one times. So if we divide 135 by 5, then the prime factorisation of the quotient will not contain 5.
135 ÷ 5 = 3 × 3 × 3
Further then perfect cube in that case is
135 ÷ 5 = 27
Hence the smallest whole number by which 135 should be divided to make it perfect cube is 5.

(iv) 192 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 3
The prime factor 3 does not appear in a group of three, so, 192 is not a perfect cube. In the factorisation 3 appears only one times. So, if we divide 192 by 3, then the prime factorisation of the quotient will not contain 3.
192 ÷ 3 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
Further the perfect cube in that case is
(192 ÷ 3 = 64)
Hence, the smallest whole numbers by which 192 should be divided to make it perfect cube is 3.

(v) 704 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 11
The prime factor 11 does not appear in a group of three. So 704 is not a perfect cube. In the factorisation 11 appears only one time. So if we divide 704 by 11, then the prime factorisation of the quotient will not contain 11.
704 ÷ 11 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
Further the perfect cube in that case is
704 ÷ 11 = 64.
Hence the smallest whole number by which 704 should be divided to make it perfect cube is 11.

Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboides will he need to form a cube?
Solution:
Parikshit’s cuboid = l × b × h
= 5 cm × 2 cm × 5cm
Now Parikshit’s volume of cube
= 5 cm × 5 cm × 25 cm
= 5 cm × 5 cm × 5 cm
The prime of factor of cuboid, 5 does not appear in a group of three. 50 cm3 is not a perfect cube. To make it cube, we need one more 5 cm. In that case,
Volume of cube = 5 cm × 5 cm × 5 cm
= 125 cm²
Hence the required smallest number by which 25 cm² should be multiplied to make a perfect cube is 5 cm.