HBSE 9th Class Science Important Questions Chapter 8 Motion

Haryana State Board HBSE 9th Class Science Important Questions Chapter 8 Motion Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 8 Motion

Very Short-Answer Type Questions

Question 1.
What do you mean by rest ?
Answer:
When a body does not change its position with respect to its surroundings, then the body is said to be at rest.

Question 2.
What is meant by motion ?
Answer:
When the position of the body continuously changes with respect to its surroundings, then the body is said to be in motion.

Question 3.
What is meant by relative motion ?
Answer:
The increase or decrease in distance between two moving bodies is known as relative motion.

Question 4.
How the motion of air can be measured ?
Answer:
The motion of air can be measured by its effect.

Question 5.
Passengers are sitting in a moving train. Tell, about which objects the passengers are in rest position and about which objects the passengers are in motion ?
Answer:
A passenger sitting in a moving train is in the state of rest in comparison of other passengers and the luggage kept in train. But the same person is in motion as compared to outsider trees and buildings.

Question 6.
Give one difference betw een the motion of living and non-living things.
Answer:
Living organisms move by themselves but external factor is required for the motion of non-living things.

Question 7.
What is distance ?
Answer:
The total path travelled by a body between initial and final points is called distance.

Question 8.
What is displacement?
Answer:
The shortest distance between the initial and final position of the body is called displacement.

Question 9.
What is the SI unit of distance and displacement ?
Answer:
The SI unit of distance and displacement is metre.

Question 10.
What is meant by reference point or origin point ?
Answer:
A fixed point with respect of which a body is at rest or in motion is known as reference point or origin point.

Question 11.
What those quantities are called, which require magnitude and direction both for their expression ?
Answer:
Those quantities which require magnitude and direction both for their expression are called vector quantities.

Question 12.
Which quantities are expressed by magnitude only ?
Answer:
Scalar quantities are expressed by magnitude only.

Question 13.
Write two examples each of vector and scalar quantities.
Answer:
Vector quantities – Velocity and displacement.
Scalar quantities – Distance and speed.

Question 14.
When an object covers equal distance in equal intervals of time, then what its speed is called ?
Answer:
When an object covers equal distance in equal intervals of time, its speed is known as uniform speed.

Question 15.
Give two examples of uniform speed.
Answer:
(i) Motion of earth
(ii) Motion of pendulum of a watch.

Question 16.
When an object covers unequal distance in equal intervals of time, then what its speed is called ?
Answer:
When an object covers unequal distance in equal intervals of time, its speed is known as non¬uniform speed.

Question 17.
Write two examples of non-uniform speed.
Answer:
(1) Train starting from a station.
(2) Birds flying in the sky.

Question 18.
Write down the formula to find out the average speed of a moving object.
Answer:
The distance travelled by an object per unit time is known as average speed.

Question 19.
What is meant by velocity ?
Answer:
The distance covered by a moving body in one second in a certain direction is called velocity.

Question 20.
What is the unit of velocity ?
Answer:
The unit of velocity is metre per second (ms’1).

Question 21.
What is the relation among distance, speed and time ?
Answer:
Distance = Speed x Time

Question 22.
What will be the velocity of an athlete, if he takes 10 seconds to cover a distance of 100 metres ?
Answer:

Question 23.
What is meant by acceleration ?
Answer:
The rate of change of velocity of a moving body is called acceleration.
a = \(\frac {v – u}{t}\)

Question 24.
What is meant by retardation ?
Answer:
The rate of decrease in velocity in a certain direction is called retardation i.e. negative acceleration s called retardation.

Question 25.
What is SI unit of acceleration ?
Answer:
SI unit of acceleration is metre Der second sauare

Question 26.
Write example ot accelerated motion.
Answer:
A body moving in a circle with uniform speed is an example of accelerated motion.

Question 27.
Choose scalar and vector from following :
(i) Delhi is at a distance of 1450 km from Mumbai.
(ii) Delhi is at a distance of 1450 km in north from Mumbai.
Answer:
(i) It is an example of scalar quantity.
(ii) It is an example of vector quantity.

Question 28.
When, a body is said to be moving with uniform acceleration ?
Answer:
If there is equal change in velocity in equal intervals of time, then the body is said to be moving with uniform acceleration.

Question 29.
Define uniform circular motion.
Answer:
When a body moves in a circular path with uniform speed, its motion is known as uniform circular motion.

Question 30.
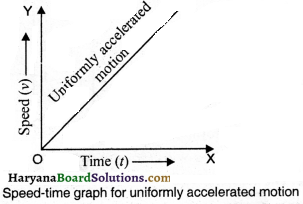
Which type of motion is shown, if the speed-time graph is a straight line ?
Answer:
It shows uniformly accelerated motion.

Question 31.
What will be the acceleration of the body, if the speed-time graph is parallel to time axis ?
Answer:
The speed of the body will uniform, therefore acceleration will be zero.

Question 32.
What shows the slope of speed-time graph of an object ?
Answer:
Acceleration of the object.

Question 33.
What the area under and between interval of speed-time graph of moving body shows ?
Answer:
The distance covered by the body in that time interval.

Question 34.
If the distance-time graph, parallel to time axis is a straight line, then average speed in different intervals will be equal or different.
Answer:
Equal.

Question 35.
If the distance-time graph of a body is a straight line, what you will say about the motion of the body ?
Answer:
The body will be in constant position.

Question 36.
If the distance-time graph of a body is a curve, then its average speed in different intervals will be different or uniform.
Answer:
The average speed will be different in different intervals.

Question 37.
If the speed of a moving body becomes 30 km/h from 0 in 2 hours, then what will be its acceleration?
Answer:
Acceleration =img= 15 kmh^-2

Question 38.
If a body is moving on circular track with uniform-speed, then which type of its motion will be ?
Answer:
Non-uniform and accelerate motion.

Question 39.
Speed of light is 3 x 10⁸ ms^-1. What will be its speed in kmh^-1 ?
Answer:
speed of light = 3 x 10⁸ms^-1 = \(\frac{3 \times 10^8 \times 3600}{1000}\)kmh^-1
= 1.08 x 10⁹kmh^-1

Question 40.
Rajdhani Express covers a distance of 1384 km in 17 hours. What will be its average speed?
Answer:

Question 41.
What will be the average speed of a car, if it covers a distance of 80 km in two hours ?
Answer:
Average speed = \(\frac {80}{2}\) = 40 kmh^-1

Question 42.
What is meant by circular motion ?
Answer:
When a body moves on circular track, its motion is known as circular motion.

Question 43.
Give two examples of circular motion.
Answer:
(1) The motion of the wheel of a vehicle.
(2) The motion of a stone tied on the end of a rope in plane circle.

Question 44.
What is meant by graph ?
Answer:
The figure representation of any information is called graph.

Question 45.
Which type of motion is shown by a freely falling object ?
Answer:
It shows a uniformly accelerated motion.

Question 46.
A stone is thrown in vertical direction, then its velocity is continuously decreasing. Why ?
Answer:
When a stone is thrown in vertical direction, its velocity continuously decreases because the acceleration due to gravity is always directed towards the centre of earth.

Question 47.
You have gone to school on 8 o’clock in morning and come back 2 o’clock in afternoon. What will be your displacement?
Answer:
Zero.

Question 48.
What will be the velocity of that object which is thrown vertically upward from the surface of earth and attains maximum height ?
Answer:
Zero.

Question 49.
What is the relation among s, u, a and t ?
Answer:
s = ut + \(\frac {1}{2}\) at².

Question 50.
What is the relation among v, u, a and t ?
Answer:
v = u + at

Question 51.
What is the relation among v, u, a and s ?
Answer:
v² – u² = 2as

Question 52.
What will be the speed of an athlete, when he completes a round in t seconds on a circular track of radius r ?
Answer:
Speed (v) = \(\frac {2πr}{t}\)

Question 53.
When there are clouds in the sky, the lightning and thundering happen in same time. First, you see the eightning After some time, the sound of thundering reaches to you. Can you tell, why it is so ?
Answer:
Because the velocity of light (3 x 10⁸ ms^-1) is much more than the velocity of sound (346 m/s).

Short Answer Type Questions

Question 1.
What is the difference between rest and motion ?
Answer:
When a body does not change its position with respect to its surroundings, it is called rest, e.g. a book lying on the table, a stone lying on the floor, etc. When the position of the body continuously changes with respect to its surroundings, it is called motion, e.g. a moving car, a running horse, etc.

Question 2.
What is meant by displacement ? When it is positive and negative ?
Answer:
The change in the position of body in a certain direction is called displacement.
The position of a body changes from x₁ to x₂, then the displacement (d) can be written as:
d = (x₂ – x₁)
The +ve and -ve signs of displacement shows the direction of change in position of body. If displacement is +ve, then body moves from left to right. If the displacement is -ve, then body moves from right to left. It is a vector quantity.

Question 3.
What is meant by speed ? Write its unit.
Answer:
Speed is the distance travelled by the body in unit time interval in any direction.

Suppose, a body covers a distance ‘s’ in time ‘ f, then its speed v = –
Unit of speed is metre per second (ms^-1). 1

Question 4.
What is meant by non-uniform motion ? Draw a graph for non-uniform motion.
Answer:
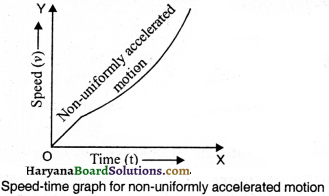
Motion of a body is said to be non-uniform, if it covers unequal distance in equal intervals of time, e.g. motion of a car on road, because its speed keeps on changing. Similarly, the motion of a train is an example of non-uniform motion, because train covers different distance in every second. Distance-time graph is shown to clear the motion of train. It is clear from the figure that speed changes with time and distance-time graph is not a straight line. It is an example of

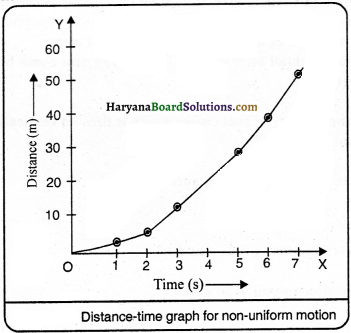
Question 5.
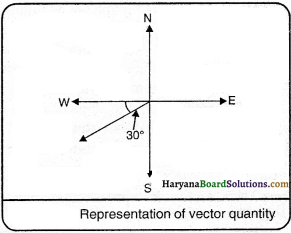
How vector is shown ?
Answer:
Vector is represented by a straight line with an arrow head over it. The length of this line is proportional to the magnitude of vector and arrow head shows the direction, which is known as the ‘head’ of vector and other end is known as the ‘tail’ of vector. For example, a velocity of 30 ms^-1, 30° in south-west direction can be shown in the form of a line carrying arrow head, as shown in figure.

Question 6.
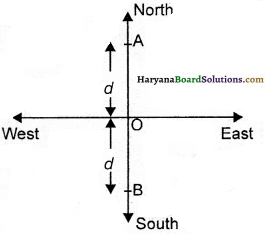
Two cars moving in opposite directions, cover an equal distance d in an hour. What will be displacement of each after an hour, if they are moving in north and south directions respectively ?
Answer:
Let O is the reference point of both cars.
The distance covered by car A from reference point O in hour in north direction = d
∴Displacement OA = d
The distance covered by car B from reference point O in hour in south direction = d
∴Displacement OB = d
Total displacement of both cars, AB = d + d = 2d

Question 7.
What is meant by graph ? What are its uses ?
Answer:
To draw the change in one physical quantity7 with respect to another physical quantity on two different axes is called graph.

Uses: The uses of graph are as follows:
(l) The relation among different quantities can be studied easily.
(2) The table of two or more than two quantities can be compared easily.
(3) It is more simple to explain quantity in graph than table.
(4) Graph represents data in less space in comparison to table which takes larger space to represent data.
(5) Quantity related to slope of graph can be found.

Question 8.
What is distance-time graph ? The distance covered by a bus in different time intervals is given in the table. Draw a distance-time graph with the help of it.

Answer:
A simple and successive method, which shows the different distances at different time of a moving body, is called distance-time graph. The distance covered by the bus in different time-intervals is shown in distance-time graph.

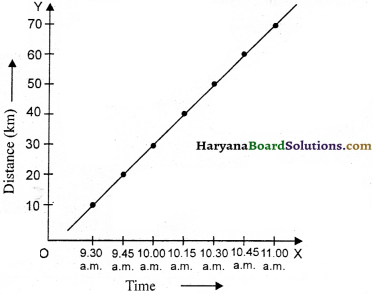
Question 9.
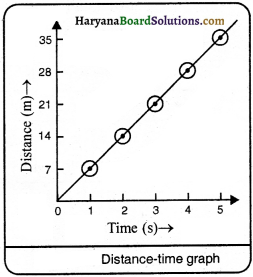
Draw distance-time graph for tw o bodies moving with uniform speed of 4 ms^-1 and 7 ms^-1 and compare it.
Answer:
We know that,
Distance = Speed x Time
(i) Distance-time graph for a body moving with uniform speed of 4 ms^-1.


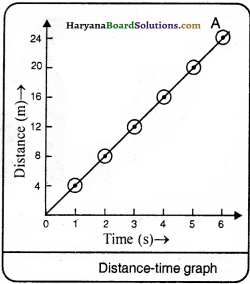
(ii) Distance-time graph for a body moving with uniform speed of 7 ms^-1.

On drawing these values on graph paper, we see that distance-time graph of given body will be as the adjacent figure.

Comparison of Graphs:
The slope of the body moving with uniform speed of 7 ms^-1 will be more than that of the body moving with uniform speed of 4 ms^-1.

Question 10.
Distance-time graph for a body is shown in figure. Is it the graph of real situation ? Give reason.
Answer:
No, this is not the graph of real situation. Reasons are as follows:
(1) According to distance-time graph, the time taken to reach that point from where it started its journey is less than the time taken by it to complete that journey.
(2) Time (t) is such a quantity which is continuously increasing. This will be larger after t = 14.

Question 11.
Distance-time table of a moving car is as follows:

Draw distance-time graph for car on the graph paper. Answer: Distance-time graph for car:

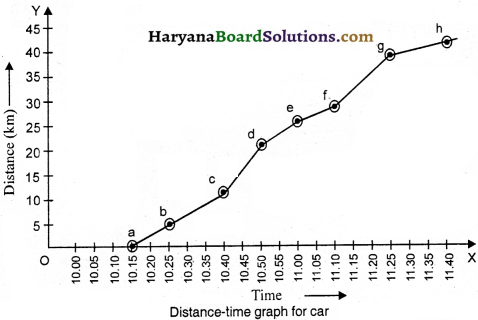
Question 12.
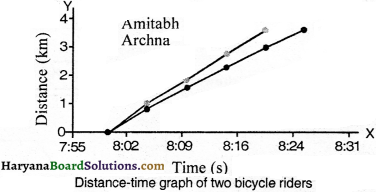
The distances covered by Amitabh and Archna by their bicycles in different times:

Show both by distance-time graph.
Answer:
The distance-time graph for both is given below:

Question 13.
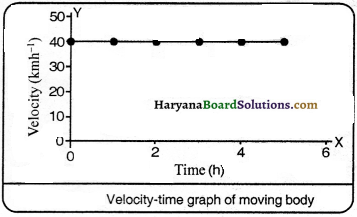
Draw velocity-time graph for a body moving with a constant velocity of 40 kmh^-1.
Answer:
To draw a velocity-time graph of a car moving with constant velocity’ of 40 kmh^-1. It means, car covers a distance of 40 km in an hour, 80 km in two hours, 120 km in 3 hours and so on, it can be seen from figure, that velocity-time graph is a straight line and parallel to time axis. It is true for all velocity-time graphs when motion is uniform.

Question 14.
How we can calculate the distance covered by a body in a given time by using velocity¬time graph ?
Answer:
Suppose the velocity-time graph of a car moving with speed of 40 kmh^-1 is as the given figure. Let us consider, we have to calculate the distance covered by the car between time and t₂. Draw perpendiculars from points t₁ and t₂ on time axis as shown in figure.

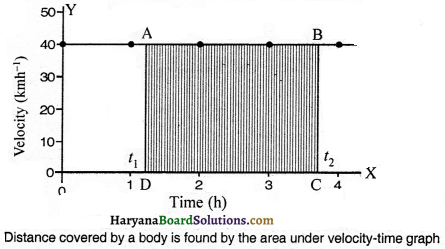
By this, we obtain a rectangle ABCD between graph and X-axis. In this rectangle side AD is equal to BC, which is equal to (t₂ -t₁), and side AB is equal to CD, which is similar to 40 kmh^-1. We know that, if a body moving with velocity (v) covers a distance (.s’) in time (?) then,
s = vt
∴ Distance covered by the car in time (t₂ – t₁) = [(40 kmh^-1) (t₂ – t₁)h]
= 40(t₂ – t₁) km
= Area of rectangle ABCD or the area under velocity-time graph shows the distance covered by the car. This is true for any velocity-time graph, whether velocity is uniform or non-uniform,

Question 15.
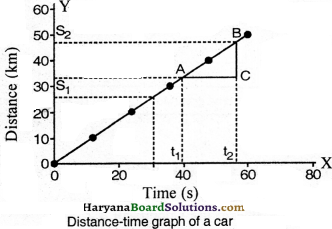
How velocity is calculated by straight-lined distance-time graph ? Explain.
Answer:
We can calculate the velocity of a car from its distance-time graph. In fig., think about the smaller part AB of distance-time graph of motion of car. We draw a straight-line from point A parallel to X-axis and from point B parallel to Y-axis to find the velocity of car. These two straight lines meet at a point C and make a AABC. Now, on graph, AC represents time-interval (t₂ – t₁), and BC is equal to distance (s₂ – s₁). It can be seen from the graph that when car move from point A to B, it covers a distance (s₂ – s₁) in time (t₂ – t₁)
Velocity of car = \(\frac{s_2-s_1}{t_2-t_1}\)

Question 16.
Show uniformly accelerated motion, non-uniformly accelerated motion and uniform retarded motion by graph.
Answer:
1. Uniformly Accelerated Motion: In uniformly-accelerated motion, speed-time graph is a straight a line.

2. Non-uniformly Accelerated Motion: In non-uniformly accelerated motion, speed-time graph is a

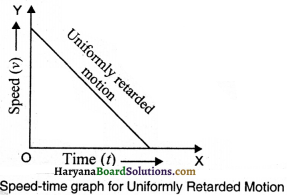
3. Uniformly Retarded Motion: In uniformly retardation, the acceleration is negative (-ve) and velocity time graph is a straight line.

Question 17.
Draw speed-time graph for a body, moving in a straight line. What the slope of this straight line show ?
Answer:
If there is equal change in the velocity of a body in equal intervals of time, then we can say that the body is moving with uniform acceleration. The speed-time graph for a body moving in a straight-line is shown in figure. If the speed of the body is v₁ at time t₁ and v₂ at time t₂, then
acceleration of the body, a = \(\frac{v_2-v_1}{t_2-t_1}\)

The time intervals (t₂ – t₁) and (t₄ -t₃) are equal as shown in figure, because the change in heights of speed are also equal. Therefore, this graph shows the motion of such a body, which is moving with uniform acceleration.
The speed-time graph of a body moving with uniform acceleration is a straight line. The acceleration of such body is the slope of this straight line.

Question 18.
How you will prove that the motion is relative ?
Answer:
In order to prove that the motion is relative, we can compare the passengers sitting in a moving bus or train with road or trees standing near the track, vehicle or persons, e.g. the passengers sitting inside the bus . or train are in rest as compared to the luggage lying inside, but are in motion as compared to outsided objects.

Question 19.
Write the difference between-
(i) vector and scalar.
(ii) uniform and non-uniform motion.
(iii) distance and displacement.
Answer:
The difference between vector and scalar:
Vector:
1. Those physical quantities which contains both direction and magnitude are known as vector quantities, e.g. velocity, displacement, force, etc.
2. Vector quantities are combined according to rule of triangle or parallelogram.
3. Vector quantities are represented by a straight line with an arrow head over it.

Scalar:
1. Those physical quantities which contain magnitude only is known as scalar quantities, e.g. distance, volume, mass, etc.
2. Scalar quantities can be combined algebraically.
3. There is no special method to represent scalar quantities.

(ii) The difference between uniform and non-uniform motion :
Uniform Motion:
When a body covers equal distance in equal intervals of time, its motion is called uniform motion, e.g. motion of earth, motion of pendulum of watch, the motion of moon around the earth.

Non-uniform Motion:
When a body covers unequal distance in equal intervals of time, its motion is called non¬uniform motion, e.g. motion of train starting from station, the motion of bus starting from bus stop, motion of cycle.

(iii) The difference between distance and displacement:

Distance:
1. The length of the path actually covered by the body is called distance.
2. It is a scalar quantity.
3. The distance between two points through different paths can be different.

Displacement:
1. The distance between the initial and final positions of the body is called displacement.
2. It is a vector quantity.
3. The value of the displacement between any two points is always same.

Question 20.
What is meant by uniform circular motion ? Justify your answer with example.
Answer:
When a body moves on circular track, it changes its direction at every point. Actually, circle is a polygon figure which has infinite sides. In figure any circular shaped track can be called a polygon of inner-sides. Therefore, a body moving in a circle with uniform speed is an example of accelerated motion. Although, there is no change in the speed of the body, but the direction of the motion of body is continuously changes. Example – Take a piece of thread and tie one stone on its one end and rotate it, it will be in a circular motion.

Numerical Questions

Question 1.
The distance between the home of a boy and school is 1.8 km, if he takes 5 minutes to reach school by cycle, then find his speed In metre/second.
Solution:
Distance (s) = 1.8 km = 1.8 x 1000 metres = 1800 metres
Time taken (t) = 5 minutes = 5 x 60 seconds = 300 seconds

= 6 ms^-1

Question 2.
A person takes 10 minutes to reach office from his home. If the office is at a distance of 3.6 km, then find the average speed of person.
Solution:
Total distance 3.6 km = 3.6 x 1000 m = 3600 metres
Total time = 10 minutes = l0 x 60seconds = 600 seconds
Total distance 3600 m

= 6 ms^-1

Question 3.
Trivendrum express moves from Guwahati at 23 : 30 hrs on Monday and after covering a distance of 3574 km, It reaches Trivendrum at 22 : 30 hrs on Thursday. Find out the average speed of
this train.
Solution:
The total distance covered by the train 3574 km
Total time between 23:30 hrs (Monday) to 22:30 hrs (Thursday) = 24 + 24 + 23 – 71h

= 50.34 kmh^-1

Question 4.
A car, starting from rest, acquire a velocity of 36 kmh’ in 10 seconds. Find out acceleration of the car.
Solution:
The car started from rest
∴ Initial velocity (u) = O
Final velocity (v) = 36 kmh^-1 = 36 x \(\frac {5}{18}\) = 10 ms^-1
Time (t) = 10 s
We know that. v = u + at
10 = 0 + a x 10
10 = 10 a
a = \(\frac {10}{10}\) = 1 ms^-1

Question 5.
A cycle moving with a velocity of 3 metre per second increase its motion with acceleration of 0.5 ms² . What will be Its velocity after 5 seconds and how much distance it will cover ¡n this time?
Solution:
Here, Initial velocity (u) = 3 ms
Acceleration (a) = 0.5 ms²
Time (t) = 5 s
Final velocity (v) = ?
Distance (s) = ?
We know that,
v = u + at = 3 + 0.5 x 5 = 3 + 2.5 = 5.5 ms^-1

(2) s = ut+ \(\frac {1}{2}\) at²
= 3 x 5 + \(\frac {1}{2}\) x 0.5 x 5 x 5
15 + 6.25 = 21.25 m

Question 6.
The uniform acceleration of a scooter is 4 ms2. How much distance will scooter cover after 10 seconds from its movement ? What will be its velocity after 10 s?
Solution:
Here,
Initial velocity of scooter (u) = 0
Acceleration (a) = 4 ms
Time (t) = 10 s
Distance (s) = ?
Final velocity (y) = ?
We know that
(1) s = ut + \(\frac {1}{2}\) at²
s = 0 x 10 + \(\frac {1}{2}\) x 4 x (10)²
s = 0 + \(\frac {1}{2}\) x 4 x 100 = 200m
(2) v = u + at = 0 + 4 x 10 = 40 ms^-1

Question 7.
A bicycle is travelling at a speed of 10 ms. The brakes are applied so as to produce a retardation of 0.5 ms2. Find, how far the bicycle travel before it is brought to rest?
Solution:
Initial velocity of bicycle (u) = 10 ms^-1
Final velocity (v) = 0
Retardation (a) = 0.5 ms^-2
We know that, v² – u² = 2as
(0)² – (10)² = 2(- 0.5) x s
– 100 = – 1s
s = 100 m

Question 8.
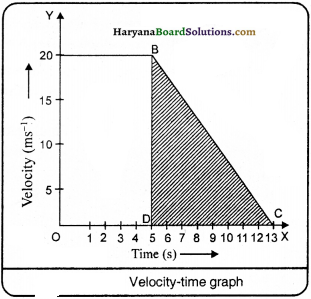
A car travels with uniform velocity 20 ms’ for 5 s. On applying brakes, the car comes to rest in 8s with uniform retardation. Draw, velocity-time graph. How far, the car will go after applying brakes?
Solution:
The velocity-time graph is shown in figure.
The distance covered by the car, after applying brakes
= area of ∆BDC = \(\frac {1}{2}\) x DC x DB
[ ∴ area of triangle = \(\frac {1}{2}\) x base x perpendicular]
= \(\frac {1}{2}\) x (13 – 5) x 20
= \(\frac {1}{2}\) x 8 x 20 = 80 m.

Question 9.
In a long running, the athletes have to move 4 rounds of running track The starting and end of race is at the same place. If the length of one round is 200 m then –
(a) how much distance is to be covered by athletes?
(b) what will be the total displacement when the athletes has completed the race?
(c) is the motion of athletes uniform or non-uniform?
(d) are the distance covered by the athletes and displacement equal, at the end of race?
Answer:
(a) The total distance to be covered by the athletes = 200 x 4 = 800 metres.
(b) Because the initial and final places of running track are at same place, therefore the total displacement of athletes = zero.
(c) The motion of athletes is non-uniform.
(a) The distance covered by the athletes at the end of race is not equal to displacement. Because –
Distance = 800 metres
Displacement = 0

Question 10.
Write the speed of following bodies in descending order –
(i) Bicycle running with a speed of 18 kmh^-1.
(ii) An athlete running with a speed of 7 ms^-1.
(iii)A car running with a speed of 2000 m min^-1
Solution:
We know that,
(i) 18 kmh^-1 = \(\frac {18000}{3600}\) ms^-1 = 5 ms^-1
(ii) 7 ms^-1
(iii) 2000 m min^-1 = \(\frac {2000}{60}\) ms^-1 = 33.33 ms^-1
∴ The descending order of speed of bodies is as follows:
(i) A car running with a speed of 2000 m min^-1.
(ii) An athlete running with a speed of 7 ms^-1.
(iii) A bicycle running with a speed of 18 kmh^-1.

Question 11.
A body moves with velocity of 2 ms^-1 for 5 seconds, in next 5 seconds, its velocity increases to 10 ms^-1 due to uniform acceleration. After that, its velocity decreases uniformly and comes in rest in 10 seconds, then
(a) draw velocity-time and distance-time graphs for the motion of the body.
(b) Show that portion in graph, where the motion is uniform and non-uniform.
(c) From graph, find the distance covered by the body after 2s and 12s and in the last lOs.
Answer:
(a) Velocity-time graph: The velocity of the body is 2 ms for first 5 seconds, which is marked
by AB in the graph. After that, it becomes 10 mst in another 5 seconds (between 5 and 10 s), which is marked
by BC in the graph. After that the body comes in rest in next 10 seconds, which is marked by CD in the graph.

(b) Distance-time graph: Because the speed of the body is not uniform. Therefore, distance-time graph is not a straight-line

From velocity-time graph, we find that the motion of the body is uniform in AB part, whereas the motion is non-uniform in BC and CD parts.
(c) (1)The distance covered by the body in 2s = 2 x 2 = 4 m.
(2) The distance covered by the body in 12 s = area of [OB’BA + BBC’C + CC’FF’]
Now, the area of rectangle OBBA = 2 x 5 = 10
Area of trapezium BB’C’C = \(\frac {1}{2}\) x (BB’ + CC’) x B’C
= \(\frac {1}{2}\) (2 + 10) x 5
= \(\frac {1}{2}\) x 12 x 5 = 30
Area of trapezium CC’FF’ = 4- (CC’ + FF’) x CF’
= \(\frac {1}{2}\) x (10 + 8) x 2 = \(\frac {1}{2}\) x 18 x 2 = 18
∴ The distance covered by the body in 12 sec 10 + 30 + 18 = 58 metres

(3) Distance covered in last lO seconds area of (trap. CC’ F’F + right-angle ∆FF’D
Now, area of trapezium CC’F’F = x (CC + FF’) x C’F’
= \(\frac {1}{2}\) x (10 + 8) x 2
= \(\frac {1}{2}\) x 18 x 2 = 18

Area of right-angle ∆FF’D = \(\frac {1}{2}\) x F’D x F’F = \(\frac {1}{2}\) x 8 x 8 = 32
∴ Distance covered in last 10 seconds = 18 + 32 = 50 metres.

Do Yourself

1. Rita takes 20 minutes to cover a distance of 3.2 km on a bicycle. Calculate her velocity in units of a kilometre minute and kilometre/hour.
Answer:
0.16 km/minute, 9.6 km/hour

2. Ahmed is driving his car with a velocity of 45 kmh^-1. How much distance will be covered in
(a) one minute and
(b) one second?
Answer:
(a) 750 metres
(b) 12.5 metres

3. Starting from rest, Saurabh paddles his bicycle to attain a velocity of 6 ms^-1 in 30 seconds. Then, he applies brakes after that the velocity of the bicycle comes down to 4 ms^-1 in next 5 seconds. Calculate the acceleration of the bicycle in both the cases.
Answer:
(a) 0.2 ms^-2
(b) -0.4 ms^-2

4. A train starting from rest attains a velocity of 108 kmh^-1 in 10 minutes. Calculate (I) acceleration (ii) distance covered by the train.
Answer:
(1) 0.5 ms²
(ii) 900 m

5. A train starting from rest attains a velocity of 72 kmh^-1 in 5 minutes. Assuming that the acceleration is uniform, find (j) acceleration of train and (ii) the distance travelled by the train while it attained this velocity.
Answer:
(i) ms^-2
(ii) 3 km

6. A car accelerates uniformly from 18 kmh^-1 to 36 kmh^-1 in 5 seconds. Calculate : (1) the acceleration and (ii) the distance covered by the car in that time.
Answer:
(i) 1 ms^-2
(ii) 37.5 m

7. The brakes applied to a car produces a negative acceleration of 6 ms2. if the car takes 2 seconds to stop after applying the brakes, calculate the distance it travels, during this time.
Answer:
12 m

8. A train covers a distance of first 30 km out of 60 km lengthy path with a uniform speed of 45 kmh^-1. By how much speed, the train will cover the remaining 30 km path so that its average speed will be 60 kmh^-1 ?
Answer:
90 kmh^-1

9. Choose right answer out of the following questions:
(a) How much distance will a car cover in 12 minutes moving with a speed of 35 kmh^-1’?
(i) 7 km
(ii) 35 km
(iii) 14 km
(iv) 28 km
Answer:
(i) 7 km

(b) If, the acceleration of the body moving with a speed of 20 ms^-1 in a straight line ¡s 4 ms^-2, then
how much speed of it will be after 2 seconds?
(1) 8 ms^-1
(ii) 12 ms^-1
(iii) 16 ms^-1
(iv) 28 ms^-1
Answer:
(iv) 28 mst

(C) The speed of a car becomes 50 kmh^-1 from 20 kmh^-1 in 10 seconds. The acceleration of this car is –
(i) 30 ms²
(ii) 3 ms²
(iii) 1 8 ms²
(iv) 0.83 ms²
Answer:
(iv) 0.83 mc²

10. A piece of wood slides down from rest on plane of 10m tong with an acceleration of 5 ms² . What will be the speed of piece of wood on reaching at the base of inclined plane?
Answer:
10 m /s

11.. A train is travelling at a speed of 90 kmh^-1 On applying brakes, a retardation of 0.5 mc² s produced. Find how far the train goes before it is brought to rest?
Answer:
625 m

12. A body covers a distance of 16 metres in 4 seconds and again covers a distance of 16 metres in 2 seconds. What will be the average speed of body?
Answer:
5.33 ms^-1

13. The odometer of a car represents 2000 km at the start of a trip and 2400 km at the end of the trip. If the trip took 8 hours then, calculate the average speed of the car in kmh’ and ms.
Answer:
50kmh^-1, 13.9 ms^-1

14. Usha swims in a 90 m long pool. She covers 180 m in one minute by swimming from one end to the other and back along the same straight path. Find the average speed and average velocity of Usha.
Answer:
Speed 3 ms^-1, Velocity = O ms^-1

15. Starting from a rest position, Rahul paddles his bicycle to attain a velocity of 6 ms1 in 30s. Then he applies brakes such that the velocity of bicycle comes down to 4 ms^-1 in the next 5s. Calculate the acceleration of the bicycle ¡n both the cases.
Answer:
0.2 m² 0.4 ms

Essay Type Question

Question 1
Prove the following equations:
(i) v = u + at²
(ii) s = ut + ut²
(iii) v² – u² = 2as
Solution:
(i) Let the initial velocity of the body = u
Time = t
Final velocity = v
Change in velocity = v – u
Rate of change in velocity (acceleration), a = \(\frac {v – u}{t}\)
at = v – u
at+u = v
v = u + at
Let the initial velocity of the body = u
Acceleration = a
and after time t, final velocity = v
1f after t sec, the distance is s, then distance (s) = average velocity x time
But, average velocity = \(\frac {v – u}{t}\)
∴Distance (s) = \(\frac {v – u}{t}\)
s = \(\frac {v – u}{2}\) x t
s = \(\frac {u + u + at}{2}\) x t [∴v = u + at]
s = \(\frac {2u + 2t}{2}\) x t
s = \(\left(\frac{2 u t+a t^2}{2}\right)=\frac{2 u t}{2}+\frac{a t^2}{2}\)
s = ut + \(\frac {1}{2}\) at²

(iii) We know that, v = u + at
Squaring both sides
(v)² = (u + at)²
v² = u² + a²t² + 2uat
v² – u² = a²t² + 2uaI
v²– u² = 2uat + a²t²

v²– u² = 2a(ut + \(\frac {1}{2}\) at²)
v²– u² = 2as

Practical Work

Experiment 1:
Describe one activity for the difference between distance and displacement.

Procedure:
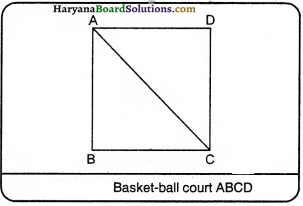
Take a metre scale and a long rope. Walk from one corner of a basket-ball court to its opposite corner way and measure with the help of scale. This will be the distance covered by you, whereas you will get displacement by putting a straight-rope from one corner to another. Suppose ABCD is basket-ball court. Distance to go from A to C AB + BC, whereas displacement = AC.

Experiment 2:
Clarify with an activity that direction of motion changes at every point on circular track

Procedure:
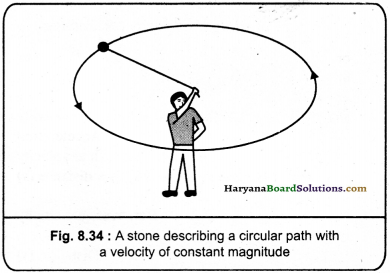
Take a piece of thread and tie a small piece of stone at one of its ends, move the stone to describe a circular path with constant speed by holding the thread at the other end as shown in figure. Now, let the stone go by releasing with thread and measure the direction of stone.

By repeating the activity for a few times and releasing the stone at different positions of circular path, check whether the direction in which the stone moves remains the same or not If you carefully note, on being released the stone moves along a straight line tangential to the circular path. This is because once the stone is’ released, it continues to move along the direction it has been moving at that instant. This shows that the direction of mot ion changes at every point when the stone was moving along the circular path.

Quick Review of the Chapter

1. A train is moving. The passengers sitting inside it, are ¡n rest compared to :
(A) other passengers
(B) the luggage in the train
(C) outsider objects
(D) other passengers and luggage in train
Answer:
(D) other passengers and luggage ¡n train

2. A train is moving. The passengers sitting inside it, are in motion as compared to :
(A) other passengers
(B) the luggage in the train
(C) outsider buildings and trees
(D) other passengers and luggage in train
Answer:
(C) outsider buildings and trees

3. If any object changes its position continuously with respect to other object, then objett is in state of
(A) motion
(B) rest
(C) constant
(D) none of these
Answer:
(A) motion

4. If any object does not change its position with respect to its surroundings, then the object is in state of
(A) motion
(B) rest
(C) circular motion
(D) movement
Answer:
(B) rest

5. Which of the following moves by themselves?
(A) living things
(B) non-living things.
(C) both living and non-living things
(D) neither living nor non-living
Answer:
(A) living things

6. SI unit of distance is:
(A) km
(B) m
(C) cm
(D) mm
Answer:
(B) m

7. WhIch of the following is a scalar quantity?
(A) momentum
(B) velocity
(C) displacement
(D) distance
Answer:
(D) distance

8. Rate of change of velocity is known as:
(A) Speed
(B) Acceleration
(C) Momentum
(D) Force
Answer:
(B) Acceleration

9. When a body covers equal distance in equal intervals of time, it is said to be
(A) uniform speed
(B) non-uniform speed
(C) average speed
(D) accelerated motion
Answer:
(A) uniform speed

10. If acceleration is in the direction of velocity, then it is called:
(A) Negative acceleration
(B) zero acceleration
(C) Positive acceleration
(D) none of these
Answer:
(C) Positive acceleration

11. If acceleration is ¡n the opposite direction of velocity then it is called:
(A) Negative acceleration
(B) zero acceleration
(C) positive acceleration
(D) none of these
Answer:
(A) Negative acceleration

12. If an object moves ¡n a circular path with uniform speed, Its motion is called: [H.B.S.E. 2020]
(A) Uniform circular motion
(B) Non-uniform circular motion
(C) Uniform curved motion
(D) Non-uniform curved motion
Answer:
(A) Uniform circular motion

13. SI unit of speed Is: [H.B.S.E. March, 2019]
(A) ms^-2
(B) ms^-1
(C) kmh^-1
(D) kms^-1
Answer:
(B) ms^-1

14. The distance covered by a moving body in one second in a certain direction is called:
(A) velocity
(B) acceleration
(C) non-uniform speed
(D) uniform speed
Answer:
(A) velocity

15. What is the relation among distance, speed and time?
(A) distance x speed = time
(B) time x distance = speed
(C) distance speed x time
(D) none of these
Answer:
(C) distance = speed x time

16. What will be the velocity of athlete if he takes 10 s to cover a distance of 100m?
(A) 100 ms^-1
(B) 10ms^-1
(C) 10 ms^-2
(D) 10 ms^-2
Answer:
(B) 10 ms^-1

17. The rate of decrease In velocity in a certain direction is:
(A) +ve acceleration
(B) – ve acceleration
(C) +ve and – ve acceleration
(D) none of these
Answer:
(B) – ve acceleration

18. The downward slope in velocity-time graph shows:
(A) accelerated motion
(B) equal motion
(C) retarded motion
(D) none of these
Answer:
(C) retarded motion

19. Rajdhanl Express covers a distance of 1384 km in 17 hours. Its average speed will be:
(A) 81.4 ms^-1
(B) 81.4 kms^-1
(C) 81.4 mh^-1
(D) 81.4 kmh^-1
Answer:
(D) 81.4 kmlf1

20. If a car covers a distance of 80 km in 2 hours, then its average speed will be:
(A) 40 kmh^-1
(B) 40 kms^-1
(C) 40 ms^-1
(D) 40 mh^-1
Answer:
(A) 40 kmh^-1

21. Cheetah is the fastest land animal and can achieve a peak velocity of 100 kmh upto a distance less than 500 m. H the cheetah spots his prey at a distance of 100 m, what ¡s the minimum time it will take to get the prey, if the average velocity attained by ¡t ¡s 90 kmh?
(A) 3s
(B) 4s
(C) 5s
(D) 6s
Answer:
(B) 4 s

22. The distance-time graph of a body is parallel to X-axis. It shows that:
(A) body is moving with non-uniform motion
(B) body is moving with accelerated motion
(C) the body is at rest
(D) body is moving with uniform motion
Answer:
(C) the body is at rest

23. By converting the speed of 2 km/h in m/s, we will get:
(A) \(\frac {5}{36}\) m/s
(B) \(\frac {5}{18}\) m/s
(C) \(\frac {5}{9}\)m/s
(D) \(\frac {50}{9}\) m/s
Answer:
\(\frac {5}{9}\)m/s

24. What is the speed of light in:
(A) 3 x 10⁸ m/s
(B) 3 x 10⁷ m/s
(C) 3 x 10¹⁰
(D) 3 x 10⁵ m/S
Answer:
(A) 3 x 10⁸ m/s

25. Which of the following is right for displacement?
(A) it cannot be zero
(B) its magnitude is more than the distance covered by the body
(C) it can be zero
(D) none of these
Answer:
(C) it can be zero

26. The odometer of any vehicle shows
(A) speed
(B) velocity
(C) distance
(D) time
Answer:
(A) speed

27. When an object Is In uniform motion, its path seems to be
(A) straight line
(B) curve
(C) irregular
(D) circular
Answer:
(A) straight line

28. During an experiment, a wireless signal from a spaceship reached ground station in 5 seconds. What Is the distance of spaceship from the ground station?
(A) 9 x 10¹⁰kjn
(B) 9 x 10¹⁰m
(C) 9 x 10¹⁰cm
(D) 9 x 10¹⁰ mm
Answer:
(B) 9 x 10¹⁰ m

29. A train is moving with a speed of 90 kmh^-1, on applying brakes, it produces a retardation of 0.5 ms². How much distance will it cover before coming to rest?
(A) 62.5 m
(B) 6.25 m
(C) 625 m
(D) 625 km
Answer:
(C) 625 m

30. A trolley while going down an inclined plane has an acceleration of 0.2 ms^-2. What will be its velocity In 3s after the starts?
(A) 0.6 ms^-1
(B) 0.6 cms^-1
(C) 0.6 mms^-1
(D) 0.6 ms^-2
Answer:
(A) 0.6 ms^-1

31. A racing car has a uniform acceleration of 4 ms^-2. What distance will it cover in lOs after the
start from rest?
(A) 20m
(B) 200m
(C) 2000m
(D) 2m
Answer:
(B) 200 m

32. A stone is thrown in vertically upward direction with a velocity of S ms⁴. If the acceleration of the stone during its motion is 10 ms², in downward direction, what will be the height aftalned by the stone?
(A) 12.5m
(B) 125m
(C) 1.25m
(D) 0.125m
Answer:
(C) 1.25 m

33. A stone Is thrown in vertically upward direction with a velocity of 5 ms. If the acceleration of the stone during its motion is 10 mr2, in downward direction, how much time will ¡t take to reach at maximum height?
(A) 0.5s
(B) 5s
(C) 5 min
(D) 0.5 mm
Answer:
(A) 0.5 s

34. An artificial satellite Is moving in a circular orbit of radius of 42,250 km. What will be Its speed, if it takes 24 hours to revolve round the earth?
(A) 3.07 ms^-1
(B) 3.07 kmh^-1
(C) 3.07 kms^-1
(D) 3.07 cms^-1
Answer:
(C) 307 kms^-1

35. An athlete completes one round of a circular track of radius r in time t, then its speed will be:
(A) 2πrt
(B) \(\frac{2 \pi r}{t}\)
(C) \(\frac{t}{2 \pi r}\)
(D) none of these
Answer:
(B) \(\frac{2 \pi r}{t}\)

36. The proper relation among s, u, t land a is:
(A) s = \(\frac{2 \pi r}{t}\)
(B) s = u + at
(C) s = ut + \(\frac {1}{2}\) at²
(D) s = uv + at
Answer:
(C) s = ut + \(\frac {1}{2}\) at²

37. The relation among y, u, a and t ¡s:
(A) v = u – at
(B) v = u + at
(C) v² = u² – at
(D) v² = u² + at
Answer:
(B) v = u + at

38. The proper relation between y, u, a and s is:
(A) v²= u² – 2as
(B) v² = 2as – u²
(C) v² – u² = 2as
(D) v² + u² = as
Answer:
(C) v² – u² = 2as