HBSE 8th Class Maths Solutions Chapter 11 Mensuration InText Questions

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 Mensuration InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 Mensuration InText Questions

Try These (Page 170)

Question 1.
(a) Match the following figures with their respective areas in the box :

(b) Write the perimeter of each shape.
Solution:

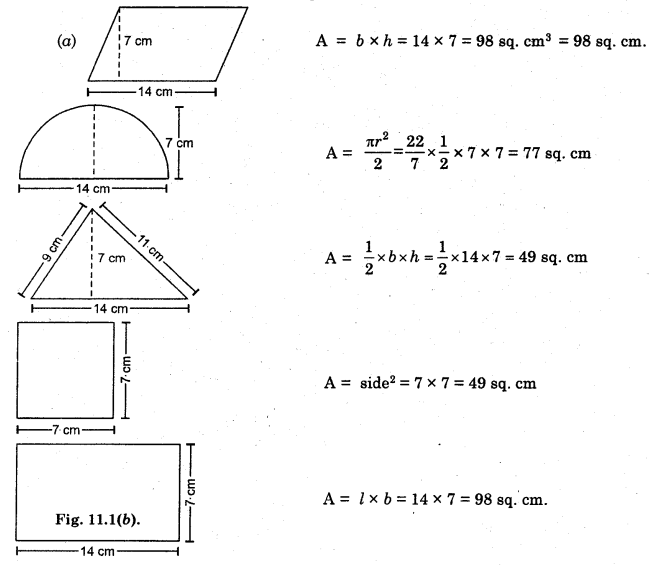
(b) (i) Perimter of parallelogram = 2(a + b) = 2(14 + b)
(ii) Perimeter of semicircle = \(\frac{2 \pi r}{2}\) = πr = \(\frac{22}{7}\) × 7 = 2 cm.
(iii) Perimeter of triangle = 14 + 11 + 9 = 34 cm.
(iv) Perimeter of square = 4 × side = 4 × 7 = 28 cm.
(v) Perimeter of rectangle = 2(l + b) = 2(14 + 7) = 2 × 21 = 42 cm.

Try These (Page 172)

Question 1.
Nazma’s sister also has a trapezium shaped plot. Divide it into three parts as shown (Fig. 11.6). Show that the area of trapezium WXYZ = h \(\frac{(a+b)}{2}\)
Solution:

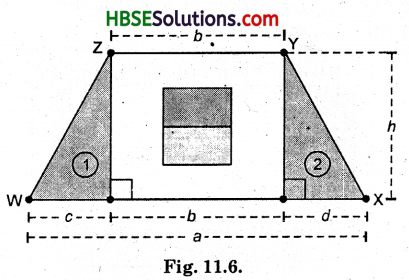
Area of trapezium = Area of △(l) + Area of rectangle + Area of △(2)

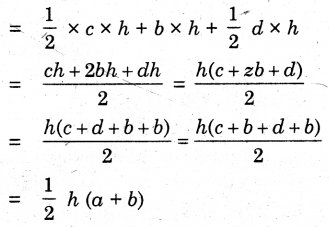
Hence, area of trapezium = \(\frac{1}{2}\) h (a + b).
Hence verified

Question 2.
If h = 10 cm, c = 6 cm, 6 = 12 cm, d = 4 cm, find the values of each of its parts separately and add to find the area WXYZ. Verify it by putting the values of h, a and b in the expression \(\frac{h(a+b)}{2}\)
Solution:
∵ Area of trapezium
= \(\frac{1}{2}\)h(a + b) = \(\frac{1}{2}\) × h(c + d + 2b)
= \(\frac{1}{2}\) × 10(6 + 4 + 2 × 12)
= \(\frac{1}{2}\) × 10(10 + 24)
= \(\frac{1}{2}\) × 10 × 34 = 170 cm²

Try These (Page 173)

Question 1.
Find the area of the following trapeziums (Fig. 11.7).

Solution:
(i) Area of trapezium
= \(\frac{1}{2}\) h (a + b)= \(\frac{1}{2}\) × 3 (9 + 7)
= \(\frac{1}{2}\) × 3 × 16 = 24 cm³.

(ii) Area of trapezium= \(\frac{1}{2}\)h(a + b)
= \(\frac{1}{2}\) × 6 × (10 + 5)
= \(\frac{1}{2}\) × 6 × 15
= 45 cm³

Try These (Page 174)

Question 1.
We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas and hence that of the parallelogram. Does this agree with the formula that you know already ? (Fig. 11.8)

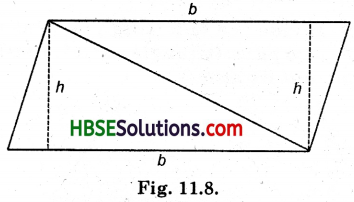
Solution: Area of parallelogram= a × h
L.H.S. = Area of parallelogram
= Area 6f triangle (l) + Area of triangle (2)
= \(\frac{1}{2}\) × b ×h + \(\frac{1}{2}\) × b × h
= \(\frac{b h+b h}{2}\) = \(\frac{2(b h)}{2}\)
= b × h
= R.H.S.
Hence verified.

Try These (Page 175)

Question 1.
Find the area of these quadrilaterals (Fig. 11.9).

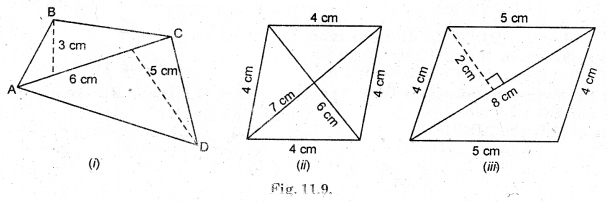
Solution:
(i) Area of quadrilateral ABCD = Area of △ABC + Area of △ACD
= \(\frac{1}{2}\) × AC × 3 + \(\frac{1}{2}\) × AC × 5
= \(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5
= 9 + 15 = 24 cm²

(ii) Area of rhombus
= \(\frac{1}{2}\) × d₁ × d₂ = \(\frac{1}{2}\) × 7 × 6
= 21 cm²

(iii) Area of parallelogram
= 2 × Area of triangle
= 2 × \(\frac{1}{2}\) × 8 × 2 = 16 cm².

Try These (Page 176)

Question 1.
(i) Divide the following polygons (Fig. 11.19) into parts (triangles and trapezium) to find out its area.

(ii) Polygon ABODE is divided into parts as shown in (Fig. 11.11). Find its area if AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, OH = 3 cm, EG = 2.5 cm.
Area of polygon ABCDE = Area of DAFB + …..
Area of △AFB = \(\frac{1}{2}\) × AF × BF
= \(\frac{1}{2}\) × 3 × 2 = …

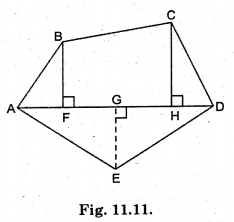
Area of trapezium FBCH
= FH × \(\frac{(\mathrm{BF}+\mathrm{CH})}{2}\)
= 3 × \(\frac{(\mathrm{2}+\mathrm{3})}{2}\)
[FH = AH – AF]
Area of △CHD = \(\frac{1}{2}\) × HD × CH = ………..
Area of △ADE = \(\frac{1}{2}\) × AD × GE = ……………..
So, the area of polygon ABODE = ………..

(iii) Find the area of polygon MNOPQR (Fig. 11.12) if MP = 9 cm, MD = 7 cm, MO = 6 cm, MB = 4 cm, MA = 2 cm.

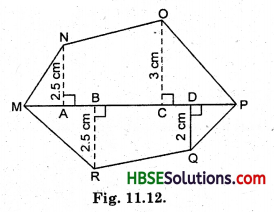
NA, OC, QD and RB are perpendiculars to diagonal MP.
Solution:
(i) (a)

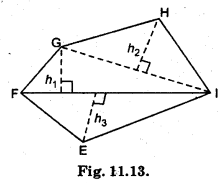
Area of polygon EFGHI
= Area of DFGI + Area of DGHI + Area of DEFI
= \(\frac{1}{2}\) FI × h₁ + \(\frac{1}{2}\) GI × h₂ + \(\frac{1}{2}\) FI × h₃.

(b)
Area of polygon MNOPQR
= Area of △NOQ + Area of △OQP + Area of △MRQ + Area of △MNQ
= \(\frac{1}{2}\) NQ × h₁ + \(\frac{1}{2}\) OQ × h₂ + \(\frac{1}{2}\) MQ × h₃ + \(\frac{1}{2}\) NQ × h₄

(ii) Area of polygon ABODE = Area of △AFB + Area of trapezium FBCH + Area of △CHD + Area of △ADE
= \(\frac{1}{2}\) × AF × BF + \(\frac{1}{2}\) (BF + CH) × FH + \(\frac{1}{2}\) × HD × CH + \(\frac{1}{2}\) × AD × EG
= \(\frac{1}{2}\) × 3 × 2 + \(\frac{1}{2}\)(2 + 3) × 3 + \(\frac{1}{2}\) × 2 × 3 + \(\frac{1}{2}\) × 8 × 2.5
[where, FH = AH – FH = 6-3 = 3 cm, HD = AD – AH = 8 – 6 = 2 cm]
= 3 + \(\frac{1}{2}\) + 3 + 10.0
= \(\frac{16}{1}\) + \(\frac{15}{2}\) = \(\frac{32+15}{2}\)
= \(\frac{47}{2}\) = 23.5 cm².

(iii) Area of polygon MNOPQR
= ar △AMN + ar trapezium ANOC + ar △COP + ar △MBR + ar, trapezium BDQR + ar △DPQ
= \(\frac{1}{2}\) × MA × AN + \(\frac{1}{2}\) (AN + CO) × AC + \(\frac{1}{2}\) × CP × CO + \(\frac{1}{2}\) × MB × BR + \(\frac{1}{2}\) × (BR + DQ) × BD + \(\frac{1}{2}\) × DP × QD
= \(\frac{1}{2}\) × 2 × 2.5 + \(\frac{1}{2}\) (2.5 + 3) × 4 + \(\frac{1}{2}\) × 3 × 3 + \(\frac{1}{2}\) × 4 × 2.5 + \(\frac{1}{2}\) × (2.5 + 2) × 3 + \(\frac{1}{2}\) × 2 × 2
where, AC = MC – MA
= 6 – 2 = 4 cm
CP = MP – MC
= 9 – 6 = 3 cm
BD = MD – MB
= 7 – 4 = 3 cm
DP = MP – MD
= 9 – 7 = 2 cm
∴ Area of polygon MNOPQR
= 2.5 + 11 + \(\frac{9}{2}\) + 5 + \(\frac{13.5}{2}\) + 2
= 2.5 + 11 + 4.5 + 5 + 6.25 + 2
= 31.25 cm².

Try These (Page 181)

Question 1.
Find the total surface area of the following cuboids (Fig. 11.30).

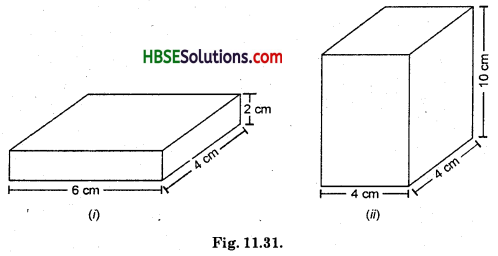
Solution:
(i) Total surface area of Cuboid = 2 (lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6)
= 2(24 + 8 + 12)
= 2 × 44 = 88 cm²

(ii)Total surface area of cuboid = 2 (lb + bh + hl)
= 2(10 × 4 + 4 × 4 + 4 × 10)
= 2(40 + 16 + 40)
= 2 × 96 = 192 cm².

Try These (Page 182)

Question 1.
Find the surface area of cube A and lateral surface area of cube B (Fig. 11.32).

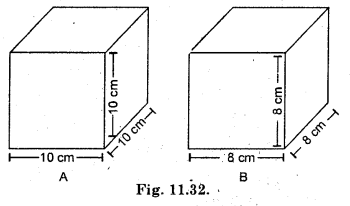
Solution:
(A) Total surface area of cube, = 6l² = 6 × (10)²
= 6 × 100 = 600 cm²
(B) Lateral surface area of cube
= 4 × (side)² = 4l²
= 4 × (8)² = 4 × 64
= 256 cm².

Try These (Page 184)

Question 1.
Find total surface area of the following cylinders (Fig. 11.33).

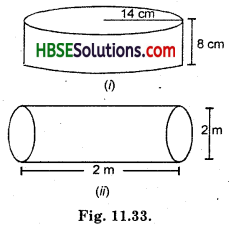
Solution:
(i) Total surface area of cylinder
= 2πr (r + h) [where r = 14, h = 8]
= 2 × \(\frac{22}{7}\) × 14(14 + 8)
= 2 × 22 × 2 × 22 = 1936 cm².

(ii) Total surface area of cylinder
= 2πr (r + h) = 2 × \(\frac{22}{7}\) × 1(1 + 2)
[∵ d = 2, r = \(\frac{d}{2}\)
where r = 1 m, h = 2 m]
= 2 × \(\frac{22}{7}\) × 1 × 3
= \(\frac{132}{7}\)
= 18.86 m²

Try These (Page 188)

Question 1.
Find the volume of the following cuboids (Fig. 11.40).

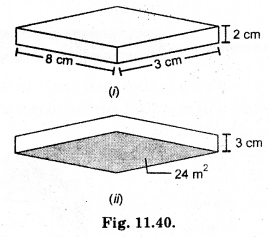
Solution:
(i) l = 8 cm, b = 3 cm, h = 2 cm
Volume of cuboid = l × b × h
= 8 × 3 × 2 = 48 cm³

(ii) l × b = 24 m2 and h = 3 cm
Volume of cuboid = l × b × h
= 24 × 3 = 72 cm³.

Try These (Page 189)

Question 1.
Find the volume of the following cubes:
(a) with a side 4 cm
(b) with a side 1.5 m.
Solution:
Volume of cube
= l³ = (4 cm)³
= 4 × 4 × 4 = 64 cm³

(ii) Volume of cube
= l³ = (1.5 cm)³
= 1.5 × 1.5 × 1.5
= 3.375 cm³.

Try These (Page 189)

Question 1.
Find the volume of the following cylinders :

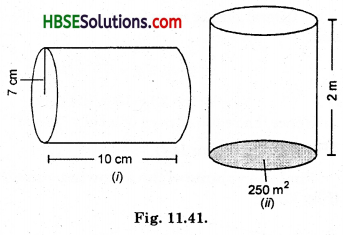
Solution:
(i) Volume of cylinder = πr²h
= \(\frac{22}{7}\) × (7)² × 10
= \(\frac{22}{7}\) × 7 × 7 × 10
= 1540 cm³.

(ii)Volume of cylinder
= Area of base ×height
= πr² × h
= 250 m² × 2 m
= 500 m³.