HBSE 7th Class Maths Solutions Chapter 3 Data Handling InText Questions

Haryana State Board HBSE 7th Class Maths Solutions Chapter 3 Data Handling InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 3 Data Handling InText Questions

Try These (Page No. 59):

Question 1.
Weigh (in kg.) atleast 20 children (girls and boys) of your class. Organise the data and answer the following questions using this data.
(i) Who is the heaviest of all ?
(ii) What is the most common weight ?
(iii) What is the difference between your weight and that of your best friend ?
Solution:
Sameer reads in class VII. Sameer’s colleage helped his organise the data in the following way:
Five conclusions:

Names	Weight (in kg.)
1. Ajay	35
2. Armaan	40
3. Ashish	35
4. Dipti	40
5. Faizaan	37
6. Govind	33
7. Jay	34
8. Kavita	36
9. Manisha	32
10. Neertg	40
11. Sameer	48
12. Rohan	50
13. Sona	42
14. Manshi	38
15. Mona	35
16. Vijay	45
17. Vinay	36
18. Saurabh	34
19. Mohan	40
20. Sanjay	40
Total	770

(a) My name is Sameer and my weight is 48 kg.
(b) My best friend is Rohan.
(c) In my class minimum weight of Manisha is 32 kg.
(d) In my class maximum weight of Rohan is 50 kg.
(e) Average weight of class VII students are 38.5 kg.
(i) Rohan is the heaviest of all.
(ii) 38.5 kg. is the most common weight. (Hi) Difference between Sameer and
Rohan
= 50 – 48 = 2 kg.

Try These (Page No. 61):

Question 2.
How would you find the average of your study hours for the whole week ?
Solution:
One a week = 7 days.
Ashish study hours for the whole week = 5, 7, 6, 8, 9, 10, 4.
Total study hours = 49 hours
∴ Mean
= \(\frac{Sum of all observations}{Number of observations}\)
= \(\frac{5+7+6+8+9+10+4}{7}=\frac{49}{7}\) = 7
∴ The average hours for study = 7 hours.

Try These (Page No. 61):

Question 1.
Find the mean of your sleeping hours during one week.
Solution:
My sleeping hours during one week = 4, 3, 5, 6, 7, 5, 6.
Total sleeping hours during one week = 36 hours.
= \(\frac{Sum of all observations}{Number of observations}\)
= \(\frac{4+3+5+6+7+5+6}{7}\)
= \(\frac{36}{7}\) = 5.14 hours.

Question 2.
Find atleast 5 numbers between \(\frac{1}{2}\) and \(\frac{1}{3}\)
Solution:

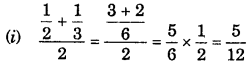
Try These (Page No. 65):

Question 1.
Find the mode of:
(i) 2, 6, 5, 3, 0, 3, 4, 3, 2, 4, 5, 2, 4.
(ii) 12, 14, 16, 12, 14, 14, 16, 14, 10, 14, IS, 14.
Solution:
(i) Arranging the numbers with same values together, we get,
0, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 6.
Mode of this data is 2, 3 and 4 because it occurs three times frequently than other observations.
(ii) Arranging the number with same values together, we get,
10, 12,12,14,14, 14, 14, 14,14, 16, 16,18.
Mode of this data is 14 because it occurs more frequently than other observations.

Try These (Page No. 65-66):

Question 1.
Find the mode of the following data :
12, 14, 12, 16, 15, 13, 14, 18, 19, 12,
14, 15, 16, 15, 16, 16,15, 17, 13, 16,
16, 15, 15, 13, 15, 17, 15, 14, 15,
13, 15, 14.
Solution:
Observations in ascending order are:
12, 12, 12, 13, 13, 13, 13, 14, 14, 14,
14, 14, 15, 15, 15, 15, 15, 15, 15,
15, 15, 15, 16, 16, 16, 16, 16, 16,
17, 17, 18, 19.
We observe that 15 is occuring ten times i.e., maximum number of times.
∴ Mode = 15

Question 1.
Heights (in cm) of 25 children are given below:
168, 165, 163, 160, 163, 161, 162,
164, 163, 162, 164, 163, 160, 163,
163, 165, 163, 162, 163, 164, 163,
160, 165, 163, 162.
What is the mode of the heights ?
What do we understand by Mode here ?
Solution:
Observations in ascending order are:
160, 160, 160, 161, 162, 162, 162,
162, 163, 163, 163, 163, 163, 163,
163, 163, 163, 163, 164, 164, 164,
165, 165, 165, 168.
We observe that 163 is occuring ten times, i.e., maximum number of times.
Hence, Mode = 163
The mode is the most frequently occuring observation, i.e., the- observation having maximum number of frequencies.

Try These (Page No. 66):

Question 1.
Discuss with your friends and give
(a) Two situations when mean would be an appropriate representative value to use and
(b) Two situations where mode would be and appropriate representative value to use.
Solution:
(a) (i) The height of 5 boys in a group are :
152 cm, 170 cm, 156 cm, 164 cm and 158 cm.
Mean = \(\frac{Sum of the given observations}{Number of observation}\)
= \(\) = 160 cm
hence, It is clear that mean is the appropriate representive value.

(ii) Mean of the first 5 whole number \(\frac{0+1+2+3+4}{5}=\frac{10}{5}\) = 2
Hence, This mean is the appropriate representive value.

(b) The mode of
(i) 5, 5, 7, 8, 8, 9, 7, 9, 10, 10, 11, 9,13.
(ii) 110, 120, 130, 120, 110, 140, 130, 120, 140,120.
Solution:
(i) In the given data, we see that the observation 9 occurs maximum number of times i.e., 3 times
Hence, mode is 9.
(ii) Since, the value 120 occurs maximum number of times, i.e. , 4 times.
Hence, mode is 120.
Hence two sutations, mode is the appropriate representative data.

Try These (Page No. 67):

Question 1.
Your friend found the median and the mode of a given data. Describe and correct your friends error if any:
35, 32, 35, 42, 38, 32, 34
Median = 42, Mode = 32.
Solution:
We arrange the data in ascending order, we get,
32,32,34, 35, 35, 38, 42.
Median is the middle observation. Therefore 35 is the median.
Here, 32 and 35 both occur two times. Therefore, they are both modes of the data.

Try These (Page No. 71-72):

Question 1.
The bar chart shows the result of a survey to test water resistant watches made by different companies.
Each of these companies claimed that their watches were water resistant. After a test the above results were revealed.

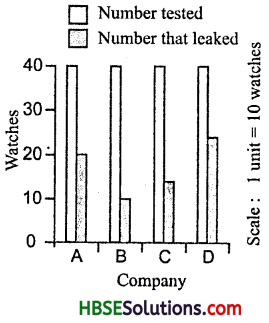
(a) Can you work a fraction of the number of watches that leaked to the number tested for each company ?
(b) Could you tell on this basis which company has better matches ?
Solution:
(a) In company A,
Number that leaked = 20,
Number that tested = 40
In company B, No. that leaked = 10,
Number that tested = 40.
In company C, No. that leaked = 12,
Number that tested = 40
In company D, No. that leaked = 22,
Number that tested =S ‘ 40
(b) B company has better matches.

Question 2.
Sale of English and Hindi books in the years 1995, 1996, 1997 and 1998 are given below. Draw a double bar graph and answer the following questions :

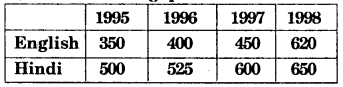
Draw a double bar graph and answer the following questions:
(i) In which year was the difference in the sale of the two languages books least ?
(ii) Can you say that the demand for English books rose faster ? Justify.
Solution:

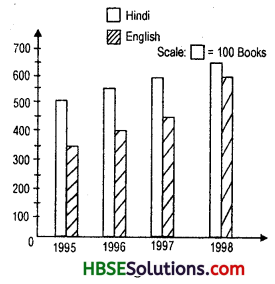
(i) 1998 (650 books – 620 books = 30 books)
(ii) Yes, 1995 to 1998 English books increases to = 50, 50, 170.
1995 to 1998 Hindi books increases to = 25, 75, 50.

Try These (Page No. 74):

Question 1.
Think of some situations, atleast 3 examples of each, that are certain to happen, some that are impossible and some that may or may not happen or Le., situations that have some chance of happening.
Solution:
(i) The sun coming up from the east. This is possible.
(ii) An elephant growing to two ft. height. This is not possible.
(iii) It will be Wednesday on 6th January. If the day on 5 th January is Monday, then on 6th January it will be Tuesday. Thus, it is impossible that the day on 6th January will be Wednesday.

Try These (Page No. 75):

Question 2.
Toss a coin 100 times and record the data. Find the number of times heads and tails occur in it.
Solution:

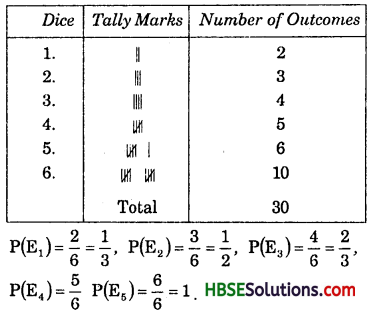
Question 3.
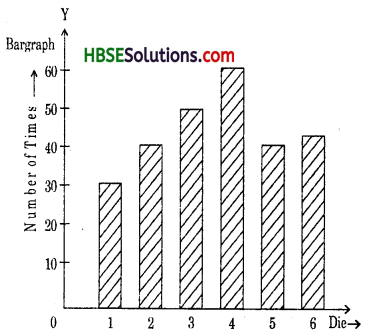
Aftaab threw a die 250 times and got the following table. Draw a bargraph for this data.

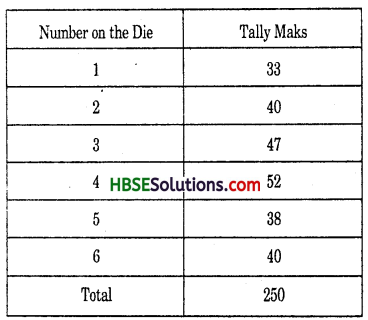
Solution:

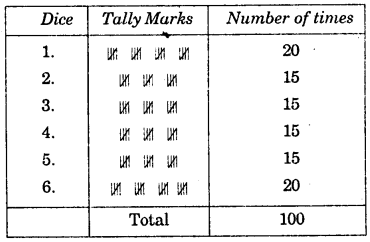
Question 4.
Throw a dice 100 times and record the data. Find the number of times 1, 2,3, 4, 5, 6 occur.
Solution:

Try These (Page No. 76):

Question 1.
Construct or think of five situations where outcomes do not have equal chances.
Solution: