HBSE 7th Class Maths Solutions Chapter 12 Algebraic Expressions Ex 12.1

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 Algebraic Expressions Ex 12.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 Algebraic Expressions Exercise 12.1

Question 1.
Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One half of the sum of number x and y.
(iii) The number z multiplied by itself.
(iv) One fourth of the product of number p and q.
(v) Number x and y both squared and added.
(vi) Number 5 added to three times and product of number m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Solution:
(i) y -z
(ii) \(\frac{1}{2}\) (x + y)
(iii) z x z =z²
(iv) \(\frac{1}{4}\) (p x q) = \(\frac{1}{4}\) (pq) = \(\frac{pq}{4}\)
(v) x² + y²
(vi) 3mn + 5
(vii) 10 – yz
(viii) ab – (a + b)

Question 2.
(i) Identify the terms and their factors in the foUowing expressions. Show the terms and factors by tree diagrams.
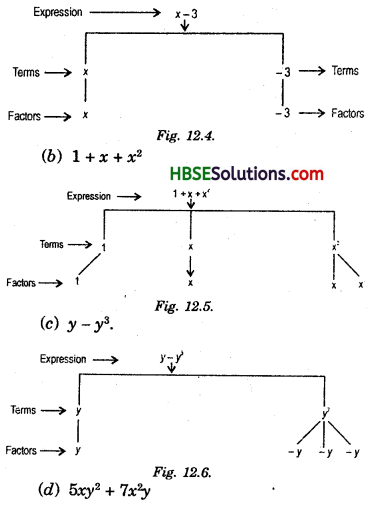
(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) -ab + 2b² – 3a²
(ii) Identify terms and factors in the expressions given below:
(a) -4x + 5
(b) -4x + 5y
(e) 5y + 3y²
(d) xy + 2x²y²
(e) pq+q
(f) 1.2ab – 2.4b + 3.6a
(g.) \(\frac{3}{4} x+\frac{1}{4} h\)
(h) \(\frac{l+m}{5}\)
[Hint: Separate l and m terms]
(j) 0.1p² + 0.2q²
(j) \(\frac{3}{4}\) (a – b) + \(\frac{7}{4}\)
[Hint: Open the brackets]
Solution:
(i) (a) x – 3: In this expression x – 3 consists two terms x and -3.

(ii) (a) – 4x + 5.
The expression (- 4x + 5) consists of two terms – 4x and 5. The term – 4x is product of – 4 and x. And the term 5 has only one factor that is 5.
Terms are – 4x and 5.
Factors are-4 andx, of-4x and factor 5 of 5.

(b) -4x + 5y
In the expression -4x + 5y The terms are – 4x and 5y and factors are- 4 and x of-4x and 5 andy of 5y.

(c) 5y + 3y²
In the expression 5y + 3y²
The terms are 5y and 3y² and factors are 5 and y of 5y, 3, y and y of 3y².

(d) xy + 2x²y²
In the expression xy + 2x²y²
The terms are xy and 2x²y²
And factors are x and y of xy and 2, x, x, y and y of 2x²y².

(e) pq + q
In the expression pq + q.
The terms are pq and q.
The factors are p and q of pq and q of q because q has only one factor.

(f) In the expression 1.2ab – 2.4b + 3.6a
The terms are 1.2ab, 2.4b and 3.6a and
factors are 1.2, a and b of 1.2ab, 2.4, and 6 of 2.4b; 3.6 and a of 3.6a.

(g) \(\frac{3}{4} x+\frac{1}{4}\)

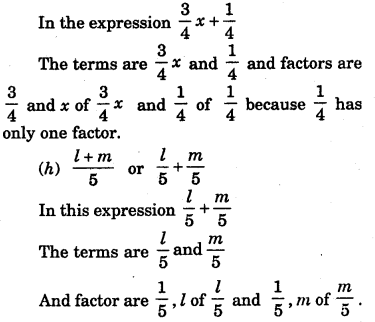
(i) 0.1p² + 0.2q²
In this expression 0.1 p² + 0.2 q²
The terms are 0.1 p² and 0.2 q² and factors are 0.1, p, p of 0.1 p² and 0.2, q, q of 0.2 q².

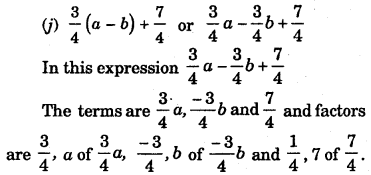
Question 3.
Identify the numerical co¬efficients of terms other than constants in the following expressions:
(i) 5-3t²
(ii) 1 + t + t² + t³
(iii) x + 2xy + 3y
(iv) 100 m + 1000 n
(v) – p²q² + 7pq
(vi) 1.2a + 0.8 b
(vii) 3.14 r²
(viii) 2(l + b)
(ix) 0.1 y + 0.01 y².
Solution:

Expression	Terms	Numerical Co-efficient
(i) 5 – 3t2	-3t2	-3
(ii) 1 + t + t2 + t3	t t2 t3	1 1 1
(iii) x + 2xy + 3y	x 2xy 3y	1 2 3
(iv) 100 m + 1000 n	100 m 1000 n	100 1000
(v) – p2q2 + 7pq	-(p2q2) 7pq	-1 7
(vi) 1.2a + 0.86	1.2a 0.86	1.2 0.8
(vii) 3.14 r2	3.14 r2	3.14
(viii) 2(l + b) = 2l + 2b	2l 2b	2 2
(ix) 0.1y + 0.01 y2	0.1y 0.01y2	0.1 0.01

Question 4.
(a) Identify terms which contain x and give the co-efficient of x.
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x +xy
(vi) 12xy² + 25
(vii) 7x + xy²
(b) Identify terms which contains y² and give the co-efficient of y².
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²
Solution:
(a)

Expression	Terms – with factor (x)	Co-efficient of x
(i) y2x + y	y2x	y2
(ii) 13y2 – 8yx	-8yx	-8y
(iii) x + y + 2	x	1
(iv) 5 + z + zx	zx	z
(v) 1 + x + xy	x xy	1 y
(vi) 12xy2 + 25	12xy2	12y2
(vii) 7x + xy2	7x xy2	7 y2

(b)

Expression	Terms with factor y2	Co-efficient of y2
(i) 8-xy2	-xy2	– X
(ii) 5y2 + 7x	5y2	5
(iii) 2xy2 – 15xy2 + 7y2	2xy2 -15xy2 7y2	2x -15x 7

Question 5.
Classify into monomials, binomials and trinomials. Give reasons for your answer:
(i) 4y – 7z
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab-a-b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²
Solution:
(i) 4y – 7z is binomial. It contain 2 terms.
(ii) y² is monomial. It contains 1 term.
(iii) x + y – xy is trinomial.lt contains 3 terms.
(iv) 100 is monomial. It contains 1 term.
(v) ab-a-b is trinomial.lt contains3 terms
(vi) 5 – 3t is binomial. It contains 2 terms.
(vii) 4p²q – 4pq² is binomial.lt contains 2 terms.
(viii) 7mn is monomial. It contains 1 term.
(ix) z² – 3z + 8 is trinomial. It contains 3 terms.
(x) a² + b² is binomial. It contain 2 terms.
(xi) z² + z is binomial. It contains 2 terms.
(xii) 1 + x + x² is trinomial. It contains 3 terms.

Question 6.
State whether the given pair of terms is of like or unlike terms.
(i) 1,100
(ii) -7x, \(\frac{5}{2}\)x
(iii) – 29x, – 29y
(iv) 14xy, 42xy
(v) 4m²p,4mp²
(vi) 12xz, 12x²z²
Solution:

Pairs	Factors	Like / Unlike Terms
(i) 1,	1	Unlike
100,	100
(ii) – 7x	– 7, x	1
5/2 x	5/2, x	Like
(iii) -29x	-29, x
-29y	– 29, y	Unlike
(iv) 14 xy	14, x, y
42 yx	42, x, y	Like
(v) 4m2p	4, m, m, p
4mp2	4, m, p, p	Unlike
(vi) 12xz	12, x, z
12x2z2	12, x, x, z, z	,       Unlike

Question 7.
Identify like terms in the following:
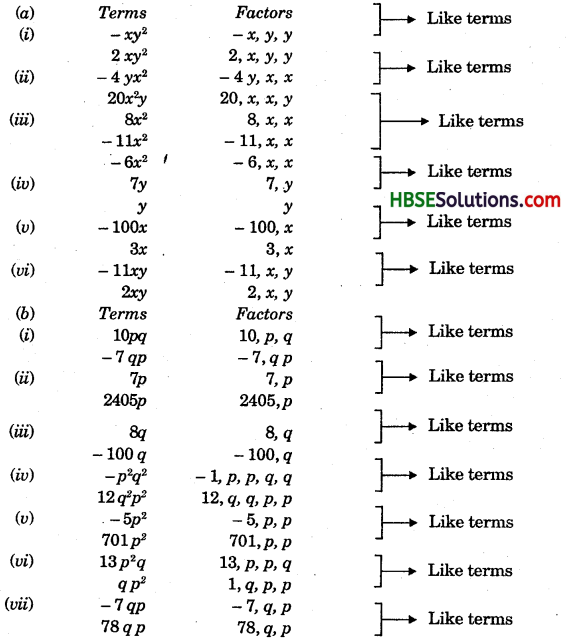
(a) – xy², – 4yx², 8x², 2xy², 7y, – 11x², – 100x, -11yx, 20x²y, -6x², y, 2xy, 3x.
(b) 10pq, 7p, 8q, – p²q², – 7qp, – 100q, – 23, 12q²p², -5P², 41, 2405p, 78qp, 13p²q, – 9pq², qp², 701P².
Solution: