HBSE 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.4

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.4 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 Perimeter and Area  Exercise 11.4

Question 1.
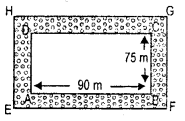
A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside and around it. Find the area of the path. Also find the area of the garden in hectare.

Solution:
Area of the garden = l x b
= 90 x 75 m² = 6750 m²
= \(\frac{6750}{10000}\)hectare = 0.675 hectare.
Area of the rect angle PQRS = l x b
= (90 + 5 + 5) x (75 + 5 + 5)
= 100 m x 85 m = 8500 m²
= \(\frac{8500}{10000}\) hectare = 0.850 hectare
∴ Area of the path = Area of the recangle PQRS – Area of the rectangle ΔBCD
= 0.850 hect – 0.675 hect.
∴ 8500-6750 = 1750 m²
= 0.175 hectare.

Question 2.
A 3m wide path runs outside around a rectangular park of the length 125 m and the breadth 65 m. Find the area of the path.

Solution:
For outside rectangle
Length = 125 + 3 + 3 = 131 m
Breadth = 65+ 3 + 3 = 71 m
Area of external rectangle = 131 x 71 = 9301 m².
For internal rectangle
Length = 125 m
Breadth = 65 m
Area of inner rectangle
= 125 x 65 = 8125 m²
Area of path = 9301 – 8125 = 1176 m².

Question 3.
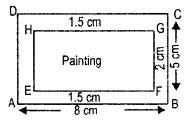
A picture is
painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.

Solution:
Let us represent the card board of length 8 cm and width 5 cm by the rectangle ABCD, and the painting by the rectangle EFGH as shown in Fig.
∵ AB = 8 cm, BC = 5 cm
∴ EF = (8-2 x 1.5) cm
= (8 – 3) cm = 5 cm
and FG = (5 — 2 x 1.5) cm
= (5 – 3) cm = 2 cm
∴ area of margin
= Area of rectangle ABCD – Area of rectangle EFGH.
= 8 cm x 5 cm – 5 cm x 2 cm
= 40 cm² – 10 cm² = 30 cm².

Question 4.
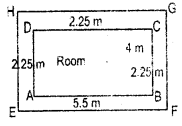
A verandah of width 2.25 m is constructed all along outside room which 5.5 m long and 4 m wide. Find
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate ofRs. 200 per m².

Solution:
Let us represent the room 5.5 m long and 4 m wide by the rectangle ABCD and the verandah 1.25 m wide all along the outside of the room by the rectangle EFGH as shown in Fig. 11.44.
Now, EF = 2.25 m + 5.5 m + 2.25 m = 10 m
and FG = 2.25 + 4 m + 2.25 m = S.5 m
Therefore the area of the verandah,
= Area of rectangle EFGH – Area of rectangle ABCD
= 10 m x 8.5 m – 5.5 m x 4 m
= 85.0 m² – 22.0 m² = 63 m².
Rate of cementing of the floor = Rs. 200 per sq. m.
∴ total cost of cementing = Rs. 200 x 63
= Rs. 6000. =Rs. 12,600.

Question 5.
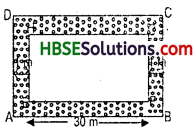
A path 1 m wide is built along the border inside a square garden of side 30 m. Find
(i) the area of the path
(ii) the cost of planting grass in the remaining portion of the garden at the rate of Rs. 40 per m³.

Solution:
Let us represent the square garden of side 30 m by the square ABCD and the path along the border by shaded region as shown as Fig. 11.48.
Area of the remaining portion of the garden = Area of square EFGH
Now, side of square EFGH
= (30 – 2 x 1) m = 28 m
So, the area of the remaining portion of garden = 28 m. x 28 m = 784 m².
Because, rate of covering the remaining
portion of the garden by grass
= Rs, 40.00 per m².
∴ Cost of covering it by grass = Rs. 40.00 x 784 = Rs. 31360.00.

Question 6.
Two cross
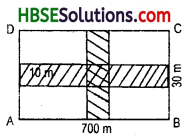
roads, each of width 10 m, cut at right angles through the centre of a rectangular park of ?
the length 700 m and the breadth 300 m and parallel to its sides. Find the area of the roads. Also find the area of park excluding cross roads. Give the answer in hectares.

Solution:
Length = 700 m
Breadth = 300 m
Area of road parallel to length
= 700 x 10 = 7000 m²
Area of road parallel to breadth
= 300 x 10 = 3000 m²
Area-of common square = 10 x 10 = 100 m²
∴ Area of roads = 7000 + 3000-100 = 9900 m².
Now, the area of park excluding the cross
road
= (Area of rectangular park – Area of roads)
= [(700 x 300) m²-9900 m²]
= (210000 m²-9900 m²)
= 200,100 m².
∵ 10000 m² = 1 hectare
∴ 1m² = \(\frac{1}{10000}\) hectare
∴ 200100 m² = \(\frac{1}{10000}\) x 200100
= \(\frac{2001}{100}\) = 20.01 hec
= 20.01 hectare.

Question 7.
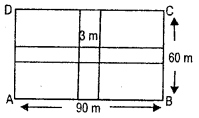
Through „ a rectangular Held of the length 90 m and the breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
(i) the area covered by the roads
(ii) the cost of constructing the roads at the rate ofRs. 110 per cm².

Solution:
For field Length = 90 m
Breadth = 60 m
width of road = 3m
Area of road parallel to length
= 90 x 3 = 270 m²
Area of road parallel to breadth
= 60 x 3 = 180 m²
Area of common square = 3 x 3 = 9 m²

(i) Area of roads = 270 + 180 – 9 = 441 m²
(ii) Rate of construction = Rs. 110 per m²
Cost of constructing roads = 110 x 441 = Rs. 48510.

Question 8.
Pragya wrapped a cord around a circular pipe of the radius 4 cm (shown below) and cut off the length required of the card. Then she wrapped it around the square box of the side 4 cm (also shown). Did she have any cord left ?

Solution:
Circumference of circulare pipe
= 2πr
= 2 x 3.14 x 4 [∵ r = 4]
= 25.12 cm
Perimeter of circular pipe
= 4 x side
= 4 x 4 cm = 16 cm
Cordleft = 25.12 — 16 = 9.12cm

Question 9.
The Fig.
11.49, represents a rectangular lawn with a circular flower bed in the middle. Find.

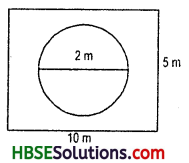
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower-bed
(iv) the circumference of the flower bed.
Solution:
(i) The area of whole rectangular lawn = l x b
length = 5m
breadth = 10 m
∴ area of the whole rectangular lawn
= l x b = 5 x 10 = 50 m².

(ii) Area of circular flower bed = πr²
= 22 x (1)²
[r = \(\frac{\mathrm{d}}{2}=\frac{2}{2}\) = 1m]
= 22 m².

(iii) Area of lawn excluding area of flower bed
= [(Area of rectangular whole land) – (Area of circular flower bed)]
= (50 – 20) m² = 30 m².

(iv) Circumference of flower-bed = 2πr
= 2 x \(\frac{22}{7}\) x 1 = \(\frac{44}{7}\) = 6.28 m (approx.)

Question 10.
Find the area of shaded portion.

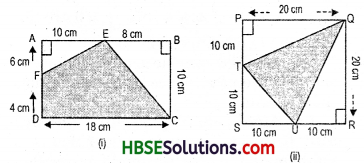
Solution:
(i) Area of rectangle ABCD = l x b
length = 10 cm
breadth = 18 cm
∴ area of rectangle = 10 x 18 = 180 cm².
Now,area of ΔEAF
= \(\frac{1}{2}\) b x h = \(\frac{1}{2}\) x 6 x 10
= \(\frac{60}{2}\) = 30 cm²,

and area of of ΔEBC
= \(\frac{1}{2}\) b x h = \(\frac{1}{2}\) x 8 x 10
= \(\frac{80}{2}\) = 40 cm²,
Area of shaded portion
= [(Area of rectangle ΔBCD) – (Area of ΔEAF + area of ΔEBC)]
= [(180)-(40 + 30)3 = [180 — 70] = 110 cm²,

(ii) Area of squares PQRS = Side x side side = 20 cm
∴ area of square = 20 x 20 = 400 cm².
Now,area of ΔTSU
= \(\frac{1}{2}\) b x h = \(\frac{1}{2}\) x 10 x 10
= \(\frac{100}{2}\) = 50cm²
Now,area of ΔQPT
= \(\frac{1}{2}\) b x h = \(\frac{1}{2}\) x 10 x 20
= \(\frac{200}{2}\) = 100cm²
andarea of ΔQRU
= \(\frac{1}{2}\) b x h = \(\frac{1}{2}\) x 10 x 20
= \(\frac{200}{2}\) = 100cm²

Area of shaded portion = [(Area of square PQRS) – (Area of ΔTSU) + (Area of ΔQPT) + (Area of ΔQRU)]
= [(400) – (50 + 100 + 100)] cm²
= (400 – 250) cm² = 150 cm².

Question 11.
Find the area of the quadrilateral ABCD. Here, AC = 22 cm, BM = 3 cm, DN = 3 cm, and BM ⊥ AC, DN ⊥ AC.

Solution:
In AABC, height = 3 cm base = 22 cm
∴ area of ΔABC = \(\frac{1}{2}\) x b x h
= \(\frac{1}{2}\) x 22 x 3
= \(\frac{66}{2}\) = 33 m²
And area ΔADC,
height = 3 cm
base = 22 cm
∴ area of ΔADC = \(\frac{1}{2}\) x b x h
\(\frac{1}{2}\) x 22 x 3 = \(\frac{66}{2}\) = 33 m²
∴ Area of quadrilaterial ABCD = Area of ΔABC + Area ΔADC
= (33 + 33) cm² = 66 cm².