Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 Understanding Elementary Shapes Ex 5.1 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 5 Understanding Elementary Shapes Exercise 5.1
Question 1.
What is the disadvantage in comparing line segments by mere observation ?
Solution:
In comparing line segments by mere observation, we cannot always be sure about the usual judgement. For example, look at A the following segments :
The difference in lengths between these two may not be obvious. Actually in this figure \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{PQ}}\) have the same lengths. This is not quite obvious.
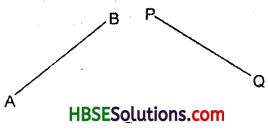
Question 2.
Why is it better to use a divider with a ruler, while measuring the length of a linesegment ? ‘
Solution:
It is better to use a divider and a ruler, while measuring the length of a line segment, because by this method we can find the exact length of a line segment.
![]()
Question 3.
Draw a line segment, say \(\overline{\mathrm{AB}}\). Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AC = AB + BC ? [Note: If A, B, C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
Solution:
On measuring, we find that
AB = 5 cm
BC = 2 cm
and AC = 3 cm
AB + BC = 5 cm + 2 cm = 7 cm
∴ AC ≠ AB + BC
![]()
But AC + CB = 3 cm + 2 cm
= 5 cm = AB.
Thus, AC + CB = AB.
Question 4.
If A, B, C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two ?
Solution:
AB = 5 cm
BC = 3cm
and AC = 8 cm
![]()
AB + BC = 5 cm + 3 cm
= 8 cm = AC
AB + BC = AC
∴ B lies between A and C.
![]()
Question 5.
Verify whether D is the mid-point of AG.
Solution:
AD = 4 – 1 = 3 units
DG = 7 – 4 = 3 units
∵ AD = DG
![]()
⇒ D is the mid-point of AG.
Question 6.
If B is the mid-point of \(\overline{\mathrm{AC}}\) and C is the mid-point of \(\overline{\mathrm{BD}}\) , where A, B, C, D lie on a straight line, say why AB = CD ?
Solution:
B is the mid-point of \(\overline{\mathrm{AC}}\)
⇒ AB = BC ………… (i)
and C is the mid-point of \(\overline{\mathrm{BD}}\)
⇒ BC = CD …(ii)
![]()
Comparing (i) and (ii), we get AB = CD.
Question 7.
Draw five triangles and measure their sides. Check in each case if the sum of two sides is ever less than the third side.
Solution:
(i) AB = BC = AC = 3 cm
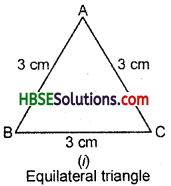
AB + BC = 3 cm + 3 cm = 6 cm
∴ AB + BC > AC
BC + AC = 3 cm + 3 cm = 6 cm
∴ BC + AC > AB
AC + AB = 3 cm + 3 cm = 6 cm
∴ AC + AB > BC.
![]()
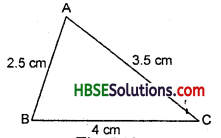
(ii) AB = AC = 3.5 cm
and BC = 3 cm

AB + BC = 3.5 cm + 3 cm
= 6.5 cm
∴ AB + BC > AC
BC + AC = 3 cm + 3.5 cm
= 6.5 cm
∴ BC + AC > AB
AC + AB = 3.5 cm + 3.5 cm
= 7 cm .
∴ AC + AB > BC.
(iii) Scalene Triangle :
AB = 2.5 cm, BC = 4 cm
AC = 3.5 cm
AB + BC = 2.5 cm + 4 cm = 6.5 cm
∴ AB + BC > AC
BC + AC = 4 cm + 3.5 cm = 7.5 cm
∴ BC + AC > AB
AC + AB = 3.5 cm + 2.5 cm = 6 cm
∴ AC + AB > BC.
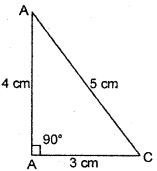
(iv) AB = 4 cm, BC = 3 cm, AC = 5 cm
AB + BC = 4 cm + 3 cm = 7 cm
AB + BC > AC
BC + AC = 3 cm + 5 cm = 8 cm
BC + AC > AB
AC + AB = 5 cm + 4 cm = 9 cm
AC + AB > BC.
![]()
(v) AB = 2.5 cm
BC = 3 cm
AC = 5 cm
AB + BC = 2.5 cm + 3 cm = 5.5 cm AB + BC > AC
BC + AC = 3 cm + 5 cm = 8 cm BC + AC > AB
AC + AB = 5 cm + 2.5 cm = 7.5 cm
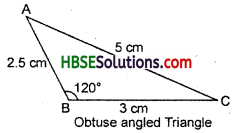
AC + AB > BC.